Экономико-математическая модель задачи

Обозначим через Х_ij количество единиц i-х ресурсов необходимых для удовлетворения j-х потребностей. Задача состоит в определении (m´n) переменных X_ij - ых, удовлетворяющих ограничениям:

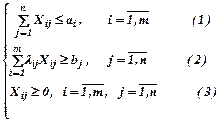
Оптимизируем функцию цели

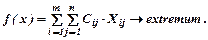(4)

В зависимости от конкретного характера задачи может варьироваться и конкретное содержание, и размерность величин a_i, b_j, C_ij, λ_ij.

Например. Если λ_ij будет представлять число единиц i-го ресурса, затраченных на удовлетворение единицы j-й потребности, тогда уравнения (1) и (2) будут иметь вид:

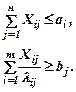
Тогда функция цели будет выглядеть

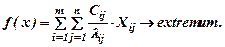
Если С_ij означает эффективность, то f(x) → max, если затраты, то функция цели f(x) → min.

Распределительную задачу можно свести к транспортной в следующих случаях:

1) когда все λ_ij при любых i и j =const. Тогда распределительная задача относится к классу простых распределительных задач­­;

2) задачи с однородными ресурсами. В этом случае наблюдается замена λ_ij в модели на λ_i;

3) задачи с пропорциональными ресурсами. Здесь существует пропорция для различных ресурсов: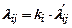

В конкретных задачах в понятиях «ресурсы», «потребности», «эффективность» и т.д. можно вкладывать различное содержание.

1) Простые распределительные задачи

Найти оптимальное распределение 3-х видов механизмов, имеющихся в количестве: а­₁ = 45 шт., а₂ = 20 шт., а₃ = 35 шт.; между 4-мя участками работ, потребности которых соответственно равны: b₁ = 10 шт., b₂ = 20 шт., b₃ = 30 шт., b₄ = 40 шт. при следующей матрице производительности (изд./час) каждого из механизмов на каждом из участков:

Нулевые элементы означают, что данный механизм на данном участке работы не может быть использован.

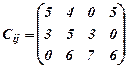
Обозначим через X_ij­ – количество механизмов i-го на j-ой работе (участке); - ресурсы (механизмы); - потребности.

- распределение всех имеющихся механизмов по всем работам - удовлетворение потребности в механизмах по всем работам - условие неотрицательности результата

- максимум производительности

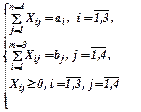
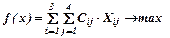
Тип механизма	Участки	Наличие
I	Х11	Х12	Х13	Х14
II	Х21	Х22	Х23	Х24
III	Х31	Х32	Х33	Х34
Потребность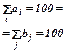

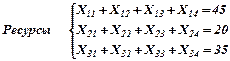
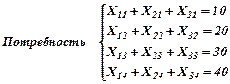
Функция цели f(x) = 5x₁₁+4х₁₂+5х₁₄+3х₂₁+ 5х₂₂+ 3х₂₃+ 6х₃₂+ 7х₃₃+ 6х₃₄→max

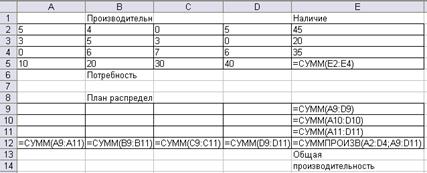
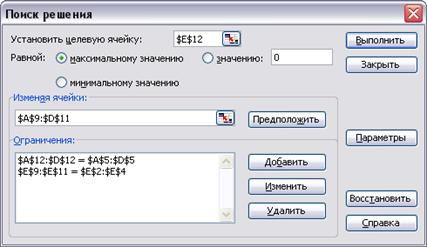
Рис. 1. Ввод математической модели в Excel

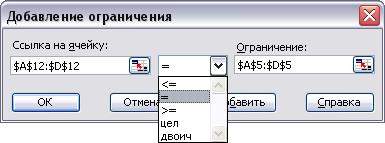
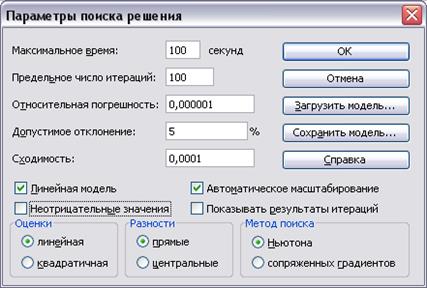
Рис. 2. Установка ограничений и параметров задачи

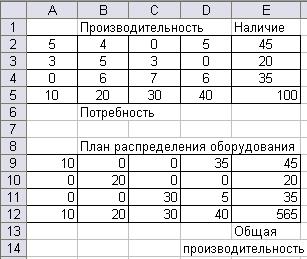
Рис. 3. Результат решения задачи

План распределения оборудования

Тип механизма	Участки	Приобретено, шт
I
II
III
Установлено, шт					Производительность 565 изд/час

2). Распределительные задачи с однородными ресурсами

Ресурсы a_i ( 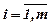) однородные и взаимозаменяемые, потребности b_j ( 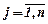) разнородные, числа λ_ij = λ_j указывают количество единиц j-й потребности, которая может быть удовлетворена единицей любого ресурса. Величины С_ij характеризуют эффективность i-го ресурса при удовлетворении им j-й потребности.

Если через X_ij обозначим количество единиц i-го ресурса, направляемых для удовлетворения j-й потребности, то мы придём к модели (1) - (4), в которой упростится ограничение (2):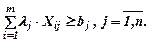

Ограничение (2) разделим почленно на λ_j и введем обозначение .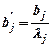

Получаем следующую систему уравнений:

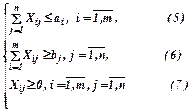
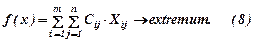
К подобным моделям (5) - (8) приводятся и задачи с разнородными, но взаимозаменяемыми ресурсами и однородными потребностями. В этом случае задаются величины λ_i, характеризующие количество единиц потребности, которая может быть удовлетворена единицей i-го ресурса.

Задача. Ресурсы угля 3-х сортов составляют 300, 800 и 400 тонн. Их теплотворная способность соответственно равна 1800, 2500 и 3000 кал/кг. Суммарные затраты на добычу и доставку каждого сорта угля до каждого из 4-х потребителей в ден. ед. за тонну задаются следующей матрицей

.

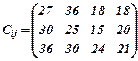Уголь сжигается в печах, принадлежащих 4-м потребителям, потребность которых составляет 750, 920, 1100 и 800 млн. калорий.

Составить план распределения ресурсов угля по печам, обеспечивающий минимизацию затрат.

Решение. Допустим Х_ij – количество угля i-го сорта поставляемое j-му потребителю. Тогда:

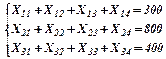
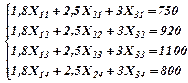
Функция цели f(x) = 27x₁₁ +36х₁₂ +18х₁₃+18х₁₄ +30х₂₁+ 25х₂₂+ 15х₂₃+ 20х₂₄ + +36х₃₁+ 30х₃₂+ 24х₃₃ +21х₃₄→ min.

Поскольку в данном виде задача не может быть приведена к транспортному виду, введем переобозначение: Х_ij – количество тепловой энергии, получаемое от i-го сорта угля в j-й печи. Тогда:

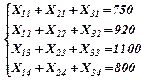Σ=3570 (потребность в энергии)

Поскольку предложение превышает спрос, необходимо ввести фиктивного потребителя, спрос которого составит 3740-3570=470 млн. кал (предложение энергии)

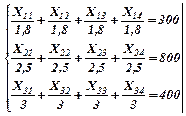
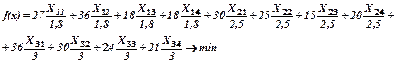
В итоге получаем задачу транспортного типа:

распределение предложения по потребителям   обеспечение потребности в энергии   минимальные общие затраты

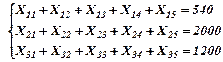
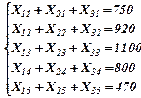
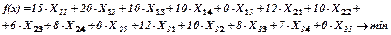
Решая задачу средствами Поиска решения в электронной таблице Excel, получим следующие результаты.

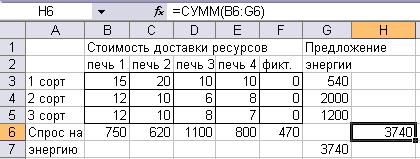
Рис. 4. Исходные данные для Поиска решения:

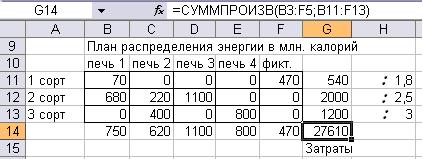
Рис. 5. Решение задачи транспортного типа в Excel

При обратном переводе поставок в тонны задача имеет уже не целочисленное решение.

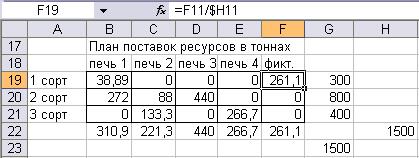
Рис. 6. Окончательный вид решения задачи

3) Распределительные задачи с пропорциональными

ресурсами

В этой задаче ресурсы 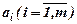и потребности 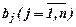неоднородные, но в матрице || λ_ij || элементы, которой устанавливают связь между единицей ресурса и потребности, строки пропорциональны:

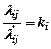, отсюда 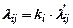для всех ,

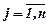где k_i – индексы i-х ресурсов (или коэффициент пропорциональности); 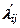- величины, относящиеся к ресурсу, выбранному за эталон.

Рассмотрим ограничение (1) задачи (1) – (4):

.

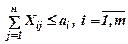Умножим левую и правую части этого выражения на k_i, получим:

.

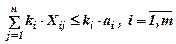Произведем замену в выражении (2):

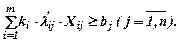
Разделим левую и правую части этого выражения на λ_ij, получим:

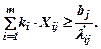
Проведем пересчет ресурсов и потребностей в условные единицы. Для этого введем обозначения:

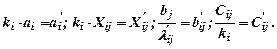
Тогда задача примет вид:

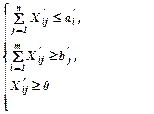
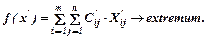
Задача. На предприятии имеется 3 типа оборудования, на котором может вырабатываться четыре вида изделий. Учитывая, что фонд рабочего времени каждой из групп оборудования соответственно равен 90, 210 и 180 станко-часов, составить такой план их загрузки, при котором общая себестоимость выпускаемой продукции являлась бы минимальной. На продукцию предприятия поступили заказы в количестве по типам продукции, соответственно 1200, 900, 1800 и 840 штук. Производительность каждого из типов оборудования и себестоимость изделий приведены в таблице:

Тип станка	Производительность станков при изготовлении продукции, шт/час	Себестоимость единицы изделий, ден. ед.	Фонд времени (станко-час)
План, шт.

распределение ресурса оборудования по изделиям

Решение. Введем обозначение Х_ij – время загрузки станков i-го типа изготовлением продукции j-го типа. Тогда модель примет вид:

Распределение фонда времени оборудования по видам продукции

выполнение плана выпуска продукции

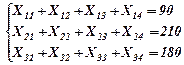
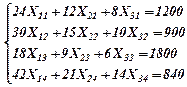
минимизация затрат:

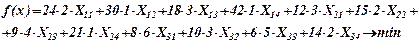
Производительность станков пропорциональна (по строкам), следовательно, задачу можно свести к транспортной:

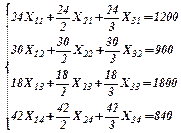
Введем переобозначения и произведем замену переменных: 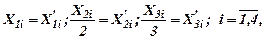тогда получаем

разделим левую и правую части выражений на величины

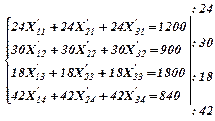
Перепишем первую систему ограничений с учетом переобозначений:

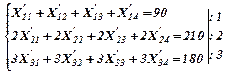
Функция цели после преобразования примет вид:

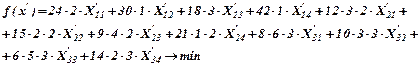
После необходимых вычислений получим:

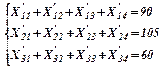
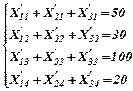
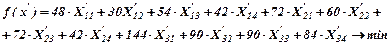
Произведем проверку: открытую или закрытую форму имеет данная задача транспортного типа. Для этого сравним суммарный спрос: 90+105+60=255 и суммарное предложение 50+30+100+20=200. Поскольку задача имеет открытую форму, и предложение превышает спрос, введем фиктивный заказ на пятый (дополнительный) вид продукции.

спрос на фиктивный вид продукции, равный разнице между суммарным предложением и суммарным спросом

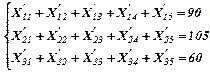
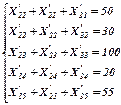
Затраты на производство фиктивной продукции будут равны нулю, что необходимо учесть в функции цели:

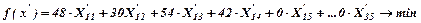
Решение задачи можно представить в виде матрицы:

или, проведя обратное преобразование, получим

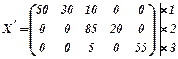
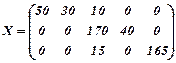
Анализ результатов: на первом станке вырабатывают первые три типа продукции в течение 50, 30 и 10 часов соответственно. На втором станке вырабатываются третий и четвёртый виды продукции, затрачивая соответственно 170 и 40 станко-часов. На третьем станке вырабатывает третий тип продукции в течении 15 часов, кроме того, на третьем станке можно было бы выработать еще дополнительный заказ, если бы он не был фиктивным. При этом остаток недоиспользованного фонда времени третьего станка – 165 часов. Функция цели f(x)= 11250 ден. ед.- минимальная себестоимость всего вырабатываемого объёма продукции.