Вращательное движение твердых тел
Модуль момента М силы F относительно некоторой оси определяется формулой 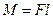 , где l - расстояние от прямой, вдоль которой действует
, где l - расстояние от прямой, вдоль которой действует
сила, до оси.
Моментом инерции материальной точки относительно некоторой оси называется величина J = m r2, где m - масса материальной точки r - ее расстояние до оси.
Момент инерции твердого тела относительно некоторой оси
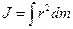 , где интегрирование должно быть распространено на весь объем тела.
, где интегрирование должно быть распространено на весь объем тела.
Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра 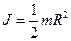 , где R - радиус цилиндра и m - его масса.
, где R - радиус цилиндра и m - его масса.
Момент инерции полого цилиндра (обруча) с внутренним радиусом R1 и внешним R2 относительно оси цилиндра 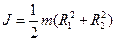 , для тонкостенного полого цилиндра R1 = R2 = R и J = т R2.
, для тонкостенного полого цилиндра R1 = R2 = R и J = т R2.
Момент инерции однородного шара радиусом R относительно оси,
проходящей через его центр, 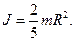
Момент инерции однородного стержня J относительно оси, проходящей через его середину перпендикулярно к нему, 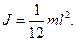
Если для какого-либо тела известен его момент инерции J0 относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, может быть найден по теореме Штейнера J = J0 + m а2, где т - масса тела и а - расстояние между осями.
Основной закон динамики вращательного движения выражается уравнением М dt=d L = d (J 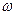 ), где М - момент сил, приложенных к телу, L - момент количества движения тела (J - момент инерции тела ,
), где М - момент сил, приложенных к телу, L - момент количества движения тела (J - момент инерции тела , 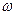 - его угловая скорость). Если J = const, то
- его угловая скорость). Если J = const, то 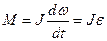 , где
, где 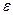 -угловое ускорение, приобретаемое телом под действием момента сил М.
-угловое ускорение, приобретаемое телом под действием момента сил М.
Кинетическая энергия вращающегося тела 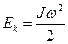 , где J –момент инерции тела и
, где J –момент инерции тела и 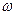 - его угловая скорость.
- его угловая скорость.
Сопоставление уравнений динамики вращательного движения с уравнениями поступательного движения дано в табл. 7.
Таблица 7
| Поступательное движение | Вращательное движение |
| Второй закон Ньютона | |
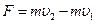 или или 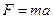 Закон сохранения количества движения Закон сохранения количества движения 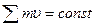 | 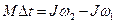 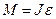 Закон сохранения момента количества движения Закон сохранения момента количества движения 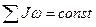 |
| Работа и кинетическая энергия | |
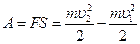 | 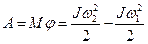 |
Элементы теории относительности
Длина l тела, движущегося со скоростью 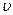 относительно некоторой системы отсчета, связана с .длиной l0 тела, неподвижного в этой системе, соотношением
относительно некоторой системы отсчета, связана с .длиной l0 тела, неподвижного в этой системе, соотношением 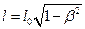 где ,
где , 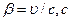 - скорость распространения света.
- скорость распространения света.
Промежуток времени 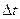 в системе, движущейся со скоростью и по отношению к наблюдателю, связан с промежутком времени
в системе, движущейся со скоростью и по отношению к наблюдателю, связан с промежутком времени 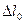 в неподвижной для наблюдателя системе соотношением
в неподвижной для наблюдателя системе соотношением
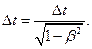
Зависимость кинетической энергии тела от скорости 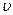 его движения дается уравнением
его движения дается уравнением 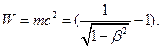
Изменение массы системы на 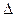 т соответствует изменению энергии системы на
т соответствует изменению энергии системы на 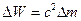 .
.
