Случай равных корней характеристического многочлена

Если характеристическое уравнение имеет два равных корня, то общее решение имеет вид:

f(n)= a∙r₁ⁿ+ β∙n∙r₁ⁿ.

Доказательство. В случае равных корней характеристического уравнения выражение f(n)= a∙r₁ⁿ+ β∙r₁ⁿ нельзя считать общим решением, так как в формуле f(n)= a∙r₁ⁿ+ β∙r₁ⁿ= r₁ⁿ∙ (a+β)= δ∙r₁ⁿ останется только одна постоянная, и выбрать её так, чтобы удовлетворить двум начальным f(0)=a, f(1)=b условиям, невозможно. Найдем второе решение, отличное от r₁ⁿ .

Если квадратное уравнение r²=С₁ r+С₂ имеет два совпадающих корня r₁= r₂ , то по теореме Виета С₁=2 r₁, а С₂= – r₁² . Поэтому уравнение записывается так:

r²= 2∙ r₁∙r+–r₁².

Тогда рекуррентное соотношение имеет вид:

f(n+2)= 2 r₁f(n+1)+ – r₁²f(n).

Докажем, что nr₁ⁿ является решением данного рекуррентного соотношения.

Подставим nr₁ⁿ в полученное рекуррентное соотношение, получим верное равенство: (n+2)r₁ⁿ⁺²=2r₁(n+1)r₁ⁿ⁺¹–r₁² nr₁ⁿ =2nr₁ⁿ⁺²+ 2r₁ⁿ⁺²–nr₁ⁿ⁺² =(n+2)r₁ⁿ⁺², значит, nr₁ⁿ является решением данного рекуррентного соотношения.

Таким образом, имеем два решения рекуррентного соотношения: r₁ⁿ и nr₁ⁿ . Общее решение будет иметь вид: f(n)= ar₁ⁿ+ βnr₁ⁿ.

Задача. Для последовательности с f(1)=0 и f(2)=8, удовлетворяющей рекуррентному соотношению f(к+2)=4f(к+1)–4f(к), выписать формулу общего члена.

Решение. Характеристическое уравнение имеет вид: r²–4r+4=0, его корни r₁=r₂=2. Общее решение рекуррентного соотношения: f(к)= a∙2^к+ β∙к∙2^к. Найдем коэффициенты a и β, пользуясь тем, что f(1)=0 и f(2)=8. Решим систему уравнений:

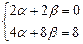
Получим a=–2 и β=2. Формула общего члена: f(n)=
–2⁽ⁿ⁺¹⁾+n∙2⁽ⁿ⁺¹⁾.

Линейные рекуррентные соотношения, порядок которых больше 2, решаются аналогично.

Задача. Найдем общее решение рекуррентного соотношения:

f(n+4)=5f(n+3)–6f(n+2)–4f(n+1)+8f(n).

Решение. Характеристическое уравнение имеет вид: r⁴-5r³+6r²+4r-8=0.

Решая его, получаем корни: r₁=2, r₂=2, r₃=2, r₄=-1.

Значит, общее решение имеет вид:

f(n)=2^n-1(a+β∙n+γ∙n²)+δ(–1)^n-1.

Асимптотики

Асимптотики – это искусство оценивания и сравнения скоростей роста функций.

Нередко в задачах на нахождение общего решения рекуррентного соотношения не требуется точное значение n-го члена, чаще бывает достаточной оценка порядка, а иногда требуется только оценка скорости роста функции f(n). Для описания роста функции используется О-символика (ввел Поль Бахман в 1894 г.).

Запись f(n)=O(g(n)) означает, что существуют положительные константы M и n₀, такие, что 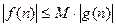для всех целых n≥n₀.

Пример 1.

Для рекуррентного соотношения f(n)=5f(n–1)–6f(n–2) с начальными членами f(1)=0 и f(2)=13 общее решение имеет вид f(n)=2ⁿ+3ⁿ. Можно сказать, что f(n)=O(3ⁿ).

Докажем это. Здесь M=2, а n₀ =1.

Неравенство 2ⁿ+3ⁿ≤3ⁿ +3ⁿ верно для всех n≥1

3ⁿ +3ⁿ =2∙3ⁿ , значит, 2ⁿ+3ⁿ≤2∙3ⁿ, следовательно, f(n)=O(3ⁿ)

Пример 2.

Для последовательности Фибоначчи, как было доказано выше, формула общего члена имеет вид: 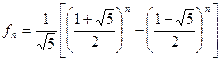. Легко доказать, что f_n=O(2ⁿ).

Соотношение f(n)=O(g(n)) называют асимптотическим соотношением, оно означает, что функция f(n) растет не быстрее, чем функция g(n). Определены еще два асимптотических отношения.

Определение 1. Функция f(x) асимптотически равна (эквивалентна) g(x) (обозначается f(x)~g(x)) при x®x0, если lim (f(x)/g(x))=1.

Если функция f(x) эквивалентна g(x), то это означает, что f(x) растет с такой же скоростью, как и g(x).

Определение 2. f(x)=o(g(x)) при x®x0, если lim (f(x)/g(x))=0.

Если f(x)=o(g(x)), то это означает, что функция f(x) растет медленнее, чем g(x).

Замечание. В соотношениях, использующих О-символику, левые и правые части не симметричны: правая часть всегда содержит меньше информации, чем левая, и поэтому нельзя в любом контексте заменять левую часть выражения правой. Например, из двух корректных асимптотических равенств х=О(х²) и х²=О(х²) не следует, что х=х².

Примеры.

1. Полином асимптотически равен своему старшему члену:

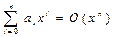при х®¥.

2. Полином f(n)=2n⁵+6n⁴+6n²+18 есть О(n⁵).

3. Функция f(n)=2ⁿ есть O(2ⁿ⁺¹) и o(5ⁿ⁺¹).

4. Для линейного рекуррентного соотношения общее решение имеет вид:

f(n)=С₁r ₁ⁿ+C₂r₂ⁿ+…+C_kr_kⁿ. Если нас интересует только асимптотическое поведение последовательности, то достаточно рассмотреть лишь члены Ci(r_i )ⁿ, у которых r_i имеет максимальное абсолютное значение среди тех членов, у которых Ci≠0.

Существуют оценки и асимптотики для комбинаторных чисел. Наиболее известна асимптотика для чисел n!, называемая формулой Стирлинга: n! ~ .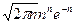

О-символику используют также для оценки сложности алгоритма. Одной из важнейших характеристик алгоритма является его временная сложность в худшем случае.

Пусть некоторая задача имеет размерность n (например, длина массива при сортировке). Обозначим через t(n) максимальное число действий, необходимое для решения задачи. Под действием понимают выполнение «простой» операции – любой арифметической операции, операции сравнения, присваивания и т. п. При этом сложность алгоритма зависит от конкретного вида команд. Поэтому при оценке интересует лишь асимптотическая сложность алгоритма, то есть порядок роста сложности при условии, что размер задачи неограниченно возрастает.

Алгоритм считается достаточно хорошим, если сложность этого алгоритма есть О(n^k) при некотором k>0. В таком случае говорят, что задача может быть решена за полиномиальное время, а сам алгоритм называется полиномиальным.