Теоретические сведения. Если об эксперименте можно сделать исключающих друг друга предположений (гипотез) и

Если об эксперименте можно сделать 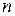исключающих друг друга предположений (гипотез) 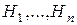и если событие А может появиться только при одной из этих гипотез, то вероятность события А вычисляется по формуле полной вероятности:

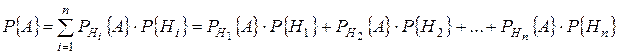
Если до эксперимента вероятности гипотез были 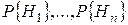, а в результате эксперимента появилось событие А, то с учетом этого условные вероятности гипотез вычисляются по формуле Байеса:

.

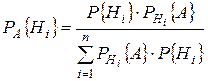Если после эксперимента, закончившегося появлением события А, производится еще один эксперимент, в котором может появиться или не появиться событие В, то условная вероятность последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние, а уточненные вероятности гипотез:

.

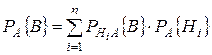Упражнения

1) Группа студентов состоит из 3 отличников, 4 хорошо успевающих и 3 занимающихся слабо. На экзамене отличники могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что он получит хорошую или отличную оценку.

2) В группе из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 2 – удовлетворительно, 1 – неудовлетворительно. В билетах 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, удовлетворительно – на 10, неудовлетворительно – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: а) отлично, б) неудовлетворительно.

3) В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0.9, для велосипедиста – 0.8, для бегуна – 0.75. Найти вероятность того, что наудачу выбранный спортсмен выполнит норму.

4) В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0.8, 0.85, 0.9, 0.95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы.

5) Имеются три урны: в первой из них 10 белых шаров и 5 черных, во второй – 8 белых шаров и 12 черных, в третьей – 20 белых шаров, черных нет. Некто выбирает наугад одну из урн и вынимает из нее шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.

6) Ученик 6 «б» класса Костя Сидоров и два его приятеля засели с рогатками в кустах школьного двора, чтобы пострелять по голубям, воркующим на карнизе окна директорского кабинета. Едва они сделали по одному выстрелу, как оконное стекло со звоном разлетелось, и всей компании пришлось спасаться бегством от выскочившего во двор завхоза. Какова вероятность того, что разбитое окно дело рук Кости Сидорова, если из 10 выстрелов он обычно попадает 8 раз, а его приятели по 7? (Примечание: случай коллективного попадания в окно исключается.)

7) Ученик 6 «б» класса Костя Сидоров и его приятель, заняв выгодную позицию вблизи школьных дверей, обстреливали снежками всех выходящих девчонок. Когда дверь в очередной раз открылась, два снежка одновременно полетели в голову застывшего на пороге завуча - Маргариты Викентьевны. Какова вероятность того, что цель была поражена, если известно, что Костя обычно попадает 8 раз из 10, а его приятель только 7?

8) Любимое занятие двухлетней девочки Кати - срезать пуговицы с одежды. Пока мама готовила кашу, Кате удалось отстричь все 5 белых пуговиц с папиной пижамы и 3 черные пуговицы с маминого вечернего платья. Одну пуговицу Катя проглотила, а остальные засунула в глубокую щель между полом и плинтусом. За этим занятием ее и застала мама. С большим трудом мама сумела выковырять из щели 2 пуговицы. Какова вероятность того, что платье можно привести в порядок, если одна запасная пуговица у мамы есть?

9) Пока мама пекла пирог, двухлетняя девочка Катя успела срезать 7 белых пуговиц с новой папиной рубашки и 3 красные пуговицы с маминого халатика. Одну пуговицу Катя проглотила, а остальные засунула в щель между книжным шкафом и стеной. Маме, заставшей Катю за этим занятием, удалось с помощью реквизированных ножниц выковырять из-за шкафа одну белую пуговицу. Остальные достать не удалось. Какова вероятность того, что проглочена пуговица с папиной рубашки?

10) В понедельник, после двух выходных, токарь Григорий вытачивает левовинтовые шурупы вместо обычных правовинтовых с вероятностью 0.5. Во вторник этот показатель снижается до среднецехового - 0.2. В остальные дни недели Григорий ударно трудится и процент брака среди изготавливаемых им шурупов составляет 10 %. При проверке недельной партии шурупов, выточенных Григорием, случайно выбранный шуруп оказался дефектным. Какова вероятность того, что шуруп изготовлен в понедельник?

11) Имеются две урны: в первой 10 белых шаров и 8 черных, во второй – 6 белых и 12 черных. Выбирается наугад одна из урн и вынимается из нее один шар. Этот шар оказался белым. Найти вероятность того, что следующий шар, который мы вынем из той же урны, будет тоже белым.