Применим выведенную выше формулу для решения задач
Задача.Для того чтобы открыть камеру хранения, используется комбинация из 4 цифр (от 0 до 9), набираемая на 4 колесиках. Сколько различных комбинаций существует?
Решение. Из условия задачи следует, что необходимо составить всевозможные комбинации по 4 элемента из данных 10. По формуле размещений с повторением получаем: 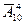 =104 = 10 000 вариантов.
=104 = 10 000 вариантов.
Задача.Сколько в n-ичной системе счисления натуральных чисел, записываемых ровно k знаками?
Решение.Если допустить записи чисел, начинающиеся с нуля, то каждое k-значное число в n-ичной системе счисления можно рассматривать как размещение с повторениями, составленное из k цифр, причем цифры бывают n видов. Получаем, что количество чисел, имеющих такую запись, равно nk.
Но натуральные числа не могут начинаться с нуля. Поэтому из полученного значения nk необходимо вычесть количество чисел, запись которых начинается с нуля. Если отбросить от этих чисел первую цифру – ноль, то получим (k–1)-значное число (быть может, начинающееся с нуля). Таких чисел по формуле для вычисления количества размещений с повторениями существует nk-1. Значит, общее количество k-значных чисел в n-ичной системе счисления равно nk – nk-1= nk(n – 1).
Размещения без повторений
Задача. Как изменится решение задачи о камере хранения, если известно, что цифры, набираемые на колесиках, различны?
Решение. Вариантов выбора первой цифры 10 (от 0 до 9). Так как повторения быть не может, то вариантов выбора второй цифры всего 9. Аналогично для выбора третьей цифры остается 8 вариантов, для выбора четвертой – 7. По правилу произведения получаем, что всего комбинаций, в которых все числа различны, 10×9×8×7=5 040.
Данная задача относится к классу задач о размещении без повторений.
Размещениями без повторений из n элементов по k называются всевозможные комбинации по k элементов, составленные из элементов данных n видов. При этом две комбинации считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.
Количество размещений без повторений обозначают 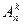 . Общее правило вычисления количества размещений:
. Общее правило вычисления количества размещений:
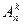 =n×(n – 1)×…×(n – k+1)=
=n×(n – 1)×…×(n – k+1)= 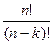 .
.
Доказательство.Действительно, на первом шаге можно выбрать любой из n имеющихся предметов. Если этот выбор уже сделан, то на втором шаге приходится выбирать из n – 1 предметов – ведь повторный выбор сделать уже нельзя. Точно так же на третьем шаге для выбора остается n – 3 предмета и т. д. Используя правило произведения, получим требуемую формулу.
Задача.В первенстве России по футболу участвуют 17 команд. Разыгрываются золотые, серебряные и бронзовые медали. Сколькими способами они могут быть распределены?
Решение. Переформулируем задачу: сколько существует комбинаций из 17 элементов по 3, если важны порядок элементов в комбинации, состав элементов, и в комбинацию не могут входить элементы одного типа. (Повторения здесь быть не может – одна и та же команда не может получить и золотую, и серебряную медаль.)
Эта задача относится к задачам на размещения без повторения. По формуле получаем: медали могут распределиться 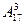 =17×16×15=4 080 способами.
=17×16×15=4 080 способами.
Задача. Автомобильные номера некоторой страны состоят из 3 букв (все буквы различны) и четырех цифр (цифры могут повторяться). Сколько максимально машин может быть в этой стране, если в её алфавите 26 букв?
Решение. Число комбинаций по 3 буквы из данных 26, при условии, что буквы не могут повторяться, определим с помощью формулы для вычисления количества размещений без повторений: 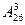 =26×25×24=15 600.
=26×25×24=15 600.
Число комбинаций по 4 цифры из данных 10, если в комбинацию могут входить одинаковые цифры, найдем с помощью формулы для вычисления количества размещений с повторениями: 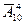 =104.
=104.
Тогда по правилу произведения различных автомобильных номеров 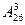 ×
× 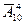 =15600×104=156×106.
=15600×104=156×106.
Перестановки
При составлении размещений без повторений из n элементов по k мы получали расстановки, отличающиеся друг от друга и составом, и порядком элементов. Но если брать расстановки, в которые входят все n элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие расстановки называют перестановками из n элементов или n-перестановками.
Перестановками из n элементов называют всевозможные комбинации из n элементов, каждая из которых содержит все элементы по одному разу. Комбинации отличаются друг от друга лишь порядком элементов.
Число n-перестановок обозначают через Рn. Общее правило вычисления количества перестановок:
Рn=Аnn=n× (n-1) × (n-2) ×...×2×1=n!
Рассмотрим несколько задач, решаемых с применением этой формулы.
Задача.Сколькими способами можно расположить на книжной полке 6 томов детской энциклопедии?
Решение.Так как на полке располагаем все 6 томов, то различные расположения отличаются только порядком, но не составом. По формуле перестановок имеем 6!=720.
Задача. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга–
Решение. На каждой вертикали и горизонтали должно стоять по одной ладье. Введем обозначения: перестановка (13256487) означает, что на первой горизонтали ладья стоит в первом поле, на второй – в третьем, на третьей – во втором и т.д. Таким образом, число искомых расположений равно количеству перестановок чисел 1, 2, 3, 4, 5, 6, 7, 8, то есть Р8=8!=40320.
Задача. Сколько существует способов разбить 6 мужчин и 6 женщин на пары для танцев?
Решение. Выстроим мужчин в одну линию в произвольном порядке. Пусть каждая женщина выбирает себе пару. Тогда количество способов разбиения на пары равно количеству способов переставить 6 различных предметов, то есть равно 6!.
Задача. Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг?
Решение. Если бы девушки стояли на месте, то получилось бы 7! способов. Так как танцующие кружатся, то их положение относительно окружающих предметов не существенно, а важно лишь взаимное расположение. Поэтому перестановки, переходящие друг в друга при кружении танцовщиц, необходимо считать одинаковыми. Из каждой перестановки можно получить еще шесть новых путем вращения. Значит, число 7! необходимо разделить на 7. Получаем 7!:7=6!=720 различных перестановок девушек в хороводе.
Перестановки с повторениями
Рассмотрим, как изменится количество перестановок, если некоторые из переставляемых предметов одинаковы.
Задача.Сколько слов можно получить, переставляя буквы слова «март»? Сколько слов можно получить, если переставлять буквы слова «мама»?
Решение. Переставляя буквы слова «март», получим 24 различные перестановки, так как все переставляемые элементы различны. Если же некоторые переставляемые предметы одинаковы, то получается меньше перестановок – некоторые перестановки совпадают друг с другом.
При перестановке букв слова «мама» имеем две пары одинаковых букв мм и аа. Сделаем их различными, дописав к одинаковым буквам различные индексы: м1а1м2а2. Рассмотрим все возможные перестановки:
м1а1м2а2 м1м2а1а2 а1а2м1м2 м1а1м2а2 м1а1а2м2 а1м1м2а2 а1м1а2м2
м2а1м1а2 м2м1а1а2 а2а1м1м2 м2а1м1а2 м2а1а2м1 а1м2м1а2 а1м2а2м1
м1а2м2а1 м1м2а2а1 а1а2м2м1 м1а2м2а1 м1а2а1м2 а2м1м2а1 а2м1а1м2
м2а2м1а1 м2м1а1а1 а2а1м2м1 м2а2м1а1 м2а2а1м1 а2м2м1а1 а2м2а1м1
Получили 24 различные перестановки, которые разбиваются на четверки одинаковых слов, если убрать индексы при буквах «м» и «а». Значит, всего различных перестановок 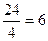 .
.
Общая задача формулируется следующим образом:
Перестановками с повторениями из n1 элементов первого типа, n2 элементов второго типа, ... , nk элементов k-го типа называются всевозможные комбинации из этих элементов, каждая из которых содержит ni элементов i-го вида. Комбинации отличаются друг от друга лишь порядком элементов.
Число перестановок с повторениями обозначают через Р(n1, n2, ..., nk). Общее правило вычисления количества перестановок с повторениями:
Р(n1, n2, ..., nk)= 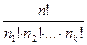
Доказательство.Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. Возьмем, например, перестановку
aa ... a bb ... b ... xx ... x,
n1 n2 nk
в которой сначала выписаны элементы первого типа, потом все элементы второго типа, …, наконец, все элементы k-го типа. Элементы первого типа можно переставлять n1! способами, это ничего не меняет. Точно так же ничего не меняют n2! перестановок элементов второго типа, ... , nk! перестановок элементов k-го типа. Перестановки элементов первого типа, второго типа и т. д. можно делать независимо друг от друга. По правилу произведения элементы перестановки можно переставлять n1!∙n2! ∙...∙nk! способами так, что она останется неизменной. То же самое верно и для любого другого расположения элементов. Поэтому множество всех n! перестановок распадается на части, состоящие из n1! ∙n2! ∙...∙nk! одинаковых перестановок каждая. Значит, число различных перестановок с повторениями, которые можно сделать из данных элементов, равно
P(n1,n2,…,nk)= 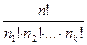
Задача. Сколькими способами можно поставить в ряд 3 красных, 4 синих и 5 зеленых кубиков?
Решение. По формуле перестановок с повторениями получаем: Р(3, 4, 5)= 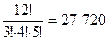 .
.
Задача. Слово – любая конечная последовательность букв русского алфавита. Сколько различных слов можно составить из слова КАСАТЕЛЬНАЯ, если необходимо использовать все буквы?
Решение. В слове имеется 3 буквы А и еще 8 различных букв. По формуле перестановок с повторениями получаем: Р(1, 1, 1, 1, 1, 1, 1, 1, 3)= 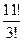 =6 652 800.
=6 652 800.
Сочетания
До сих пор при составлении комбинаций из элементов различных типов нас интересовал порядок расположения элементов. Но некоторый класс задач приводит к составлению комбинаций, в которых порядок элементов совершенно не важен.
Задача.Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?
Решение. Это задача на размещения без повторений. Ответ: 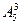 =5×4×3=60 способов составить флаг.
=5×4×3=60 способов составить флаг.
Задача. Сколькими способами можно выбрать три краски из имеющихся пяти?
Решение. В данном случае порядок выбора красок не важен. Поэтому количество способов выбора красок, полученное в предыдущей задаче, необходимо разделить на 3! – количество способов переставить выбранные краски. Ответ: 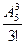 =10.
=10.
Эта задача относится к классу задач о сочетаниях.
Сочетаниями из n элементов по k называют всевозможные комбинации по k элементов, составленные из данных n элементов. Комбинации отличаются друг от друга составом, но не порядком элементов.
Количество сочетаний из n элементов по k обозначают 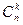 .
.
Формула для вычисления числа сочетаний получается из формулы для вычисления количества размещений. Составим сначала все k-сочетания из n элементов, а потом переставим входящие в каждое сочетание элементы всеми возможными способами. При этом получатся все k-размещения из n элементов, причем каждое только по одному разу. Элементы каждого k-сочетания можно переставить k! способами, а число этих сочетаний равно 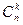 . Значит, справедлива формула
. Значит, справедлива формула 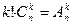 . Получаем
. Получаем 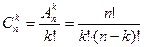
Задача. Два филателиста хотят обменяться марками. У одного для обмена есть 7 марок, у другого – 5. Сколькими способами они могут поменять две марки одного на две марки другого?
Решение. Первый филателист должен выбрать 2 марки из 7. Он может это сделать 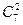 способами. Второй должен выбрать 2 марки из 5. Он может это сделать
способами. Второй должен выбрать 2 марки из 5. Он может это сделать 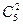 способами. По правилу произведения получаем
способами. По правилу произведения получаем 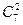 ×
× 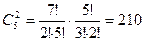 способов совершить обмен.
способов совершить обмен.
Задача. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди них окажется ровно три туза?
Решение. Необходимо выбрать трех тузов и семь «не тузов». Всего в колоде 4 туза. Поэтому выбрать из них 3 можно 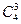 способами. «Не тузов» в колоде 48. Выбрать из них 7 можно
способами. «Не тузов» в колоде 48. Выбрать из них 7 можно 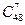 способами. По правилу произведения получаем
способами. По правилу произведения получаем 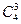 ×
× 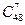 =
= 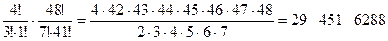 способов выбрать из колоды 10 карт так, что среди них будет ровно три туза.
способов выбрать из колоды 10 карт так, что среди них будет ровно три туза.
Свойства чисел 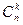
Числа 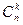 обладают рядом замечательных свойств. Эти свойства можно доказывать по-разному. Можно прямо воспользоваться формулой
обладают рядом замечательных свойств. Эти свойства можно доказывать по-разному. Можно прямо воспользоваться формулой 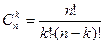 . Однако часто удается получить доказательство из комбинаторных соображений.
. Однако часто удается получить доказательство из комбинаторных соображений.
1 свойство: P(k, n-k) = 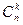
Доказательство.
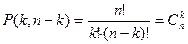
Комбинаторное доказательство.
Поставим по порядку все n элементов, из которых составляют сочетания, и зашифруем каждое сочетание комбинацией из n нулей и единиц. Каждому k-сочетанию соответствует комбинация из k единиц и n – k нулей, и наоборот. Отсюда и следует, что число сочетаний из n элементов по k совпадает с числом перестановок с повторениями из к элементов одного вида (единиц) и n – k элементов другого (нулей).
2 свойство – свойство симметричности 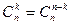
Доказательство.
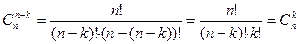 .
.
Комбинаторное доказательство.
Если выбрать из n различных предметов некоторое k-сочетание, то останется дополнительное (n – k)-сочетание, а дополнительным к (n – k)-сочетанию является исходное k-сочетание. Таким образом, k-сочетание и (n – k) сочетание образуют взаимно дополнительные пары, поэтому число этих сочетаний одно и то же.
3 свойство – основное свойство 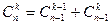
Доказательство.
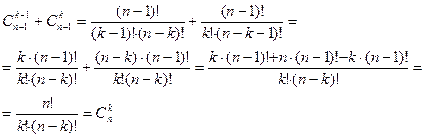
Комбинаторное доказательство.
Составим k-сочетание из n элементов а1, а2, …,an и разобьем их на два класса. В первый из них войдут сочетания, содержащие элемент an, во второй – не содержащие этого элемента. Если из любого сочетания первого класса откинуть элемент аn, то останется (к –1)-сочетание, составленное из элементов а1, а2, …, an-1. Число таких сочетаний равно 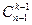 . Поэтому в первый класс входит
. Поэтому в первый класс входит 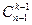 комбинаций. Сочетания второго класса являются k-сочетаниями, составленными из элементов а1, а2, …,an-1. Поэтому их число равно
комбинаций. Сочетания второго класса являются k-сочетаниями, составленными из элементов а1, а2, …,an-1. Поэтому их число равно 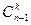 . Поскольку любое k-сочетание принадлежит одному и только одному из этих классов, а общее число этих сочетаний равно
. Поскольку любое k-сочетание принадлежит одному и только одному из этих классов, а общее число этих сочетаний равно 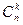 , то, используя правило сложения, приходим к искомому равенству.
, то, используя правило сложения, приходим к искомому равенству.
4 свойство: 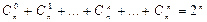
Комбинаторное доказательство.
2n – число всех размещений с повторениями из элементов двух типов. Разобьем эти размещения на классы, отнеся в k-ый класс те, в которые входят k элементов первого типа и n–k элементов второго типа. Размещения k-го типа – это не что иное, как всевозможные перестановки из k элементов первого типа и n–k элементов второго типа. Число таких перестановок равно P(k, n–k)=C(n, k). По правилу суммы общее число размещений всех классов равно 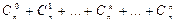 . С другой стороны, это же число равно 2n.
. С другой стороны, это же число равно 2n.
5 свойство: 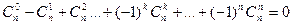
Комбинаторное доказательство.
Выпишем все сочетания из n элементов а1, …,аn и сделаем следующее преобразование: к сочетанию, не содержащему элемент а1, допишем его, а из сочетаний, куда оно входит, вычеркнем. Легко проверить, что при этом снова получаются все сочетания, и притом по одному разу. Но при этом преобразовании все сочетания, имевшие четное число элементов, превратятся в сочетания, имеющие нечетное число элементов, и обратно. Значит, сочетаний с четным и нечетным количеством элементов одинаковое количество (пустое сочетание тоже входит в рассмотрение). Это и выражает данная формула.
Задача. На окружности отмечено 11 точек. Сколько существует многоугольников с вершинами в отмеченных точках?
Решение. Первый способ. Существует 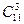 треугольников с вершинами в отмеченных точках,
треугольников с вершинами в отмеченных точках, 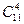 – четырехугольников,
– четырехугольников, 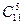 – пятиугольников, … ,
– пятиугольников, … , 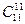 – одиннадцатиугольников. Таким образом, по правилу суммы всего многоугольников
– одиннадцатиугольников. Таким образом, по правилу суммы всего многоугольников 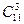 +
+ 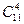 +
+ 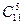 +…+
+…+ 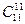 . Из четвертого свойства следует, что это выражение равно 211–
. Из четвертого свойства следует, что это выражение равно 211– 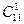 –
– 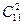 =1 982.
=1 982.
Второй способ. Любая из одиннадцати точек либо является вершиной рассматриваемого многоугольника, либо не является. Всего вариантов 211. Но одна или две точки не могут составлять многоугольник. Остается 211– 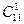 –
– 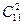 вариантов многоугольников с вершинами в отмеченных точках.
вариантов многоугольников с вершинами в отмеченных точках.
Сочетания с повторениями.
Задача. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение. Эта задача не является задачей на размещения с повторениями, так как порядок, в котором укладывают пирожные в коробку, несущественен. Поэтому она ближе к задачам на сочетания. Но от задач на сочетания она отличается тем, что в комбинации могут быть повторяющиеся элементы. Такие задачи называют задачами на сочетания с повторениями.
Чтобы решить задачу, поступим следующим образом. Зашифруем каждую покупку с помощью нулей и единиц. Сначала напишем столько единиц, сколько куплено наполеонов. Потом, чтобы отделить наполеоны от эклеров, напишем нуль, затем – столько единиц, сколько куплено эклеров, и т. д. Например, если куплено 3 наполеона, 1 эклер, 2 песочных и 1 слоеное пирожное, то получим такую запись: 1110101101. Ясно, что разным покупкам соответствуют разные комбинации из 7 единиц и 3 нулей. Обратно, каждой комбинации 7 единиц и 3 нулей соответствует какая-то покупка.
Таким образом, число различных покупок равно числу перестановок с повторениями, которые можно составить из 7 единиц и 3 нулей. А это число равно P(7,3)=120.
К тому же самому результату можно было прийти и другим путем, а именно: расположим в каждой покупке пирожные в таком порядке: наполеоны, эклеры, песочные и слоеные, а потом перенумеруем их. Но при нумерации будем к номерам эклеров прибавлять 1, к номерам песочных – 2, к номерам слоеных – 3. К номерам наполеонов ничего прибавлять не будем. Например, пусть куплено 2 наполеона, 3 эклера, 1 песочное пирожное и 1 слоеное. Тогда эти пирожные нумеруются так: 1, 2, 4, 5, 6, 8, 10. Ясно, что самый большой номер может быть 10, самый маленький – 1, а кроме того, ни один из номеров не повторяется, причем они образуют возрастающую последовательность. Обратно, каждой возрастающей последовательности из 7 чисел соответствует некоторая покупка. Например, последовательность 2, 3, 4, 5, 7, 8, 9 соответствует покупке из 4 эклеров и 3 песочных пирожных. Чтобы убедиться в этом, надо отнять от заданных номеров числа 1, 2, 3, 4, 5, 6, 7. Мы получим числа 1, 1, 1, 1, 2, 2, 2. Но 1 мы прибавляли к номерам эклеров, а 2 – к номерам песочных.
Отсюда, общее число покупок равно числу возрастающих последовательностей из 7 чисел от 1 до 10. А число таких последовательностей равно C(10,7)=120.
Сочетаниями с повторениями изn элементов по k называют всевозможные комбинации, составленные из элементов n видов по k элементов в каждой. Комбинации считаются различными, если они отличаются составом, но не порядком входящих в них элементов. В комбинацию могут входить элементы одного вида.
Количество сочетаний с повторениямиизn элементов по k обозначают 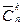 . Общее правило вычисления количества сочетаний с повторениями:
. Общее правило вычисления количества сочетаний с повторениями:
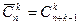
Доказательство.Зашифруем каждую комбинацию с помощью нулей и единиц: для каждого типа напишем столько единиц, сколько предметов этого типа входит в комбинацию, а предметы различных типов отделим нулями. При этом число единиц будет k, а число нулей – n–1. Различным комбинациям будут соответствовать различные перестановки с повторениями из k элементов первого вида и n–1 элементов второго вида, а каждой перестановке с повторениями – своя комбинация. Итак, 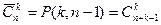 .
.
Встречаются задачи, в которых на сочетания с повторениями накладывается дополнительное условие, например, когда в комбинацию обязательно должны входить элементы r фиксированных типов, где r≤n. Эта задача легко сводится к уже решенной. Для того чтобы обеспечить присутствие заданных r типов, возьмем с самого начала по одному элементу каждого такого типа. Тем самым в k-сочетании окажутся заняты r мест. Поэтому ответом на задачу будет число 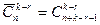 . В частности, если требуется, чтобы в каждом сочетании был элемент каждого из типов (n≤k), то получится
. В частности, если требуется, чтобы в каждом сочетании был элемент каждого из типов (n≤k), то получится 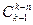 .
.
Задача. Сколько существует различных бросаний двух одинаковых кубиков?
Решение. Переформулируем задачу. Всего при подбрасывании одного кубика возможны шесть ситуаций – имеем предметы шести различных типов. Подбрасывают два кубика, следовательно, из данных шести типов предметов необходимо выбрать два, причем нас не интересует порядок выбора, и допускается выбор одинаковых предметов. Таким образом, это задача на сочетания с повторением. По формуле для вычисления количества сочетаний с повторением имеем 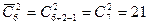 различных бросаний двух одинаковых кубиков.
различных бросаний двух одинаковых кубиков.
Комбинаторика разбиений
Многим комбинаторным задачам можно придать вид стандартной схемы. В этой схеме объекты (предметы) помещаются в ящики. Из-за наложения различных ограничений получаются различные задачи. Рассмотрим некоторые из них.
Имеется n1 предметов одного сорта, n2 – другого, ... , nk – k-го сорта. Сколькими способами можно разложить их в два ящика?
Так как в каждый ящик может попасть от 0 до ni предметов i-го сорта (во второй все оставшиеся), по правилу произведения получаем (n1+1)∙(n2+1)∙...∙(nk+1) способов раскладки.
Задача. Двое ребят собрали 10 ромашек, 15 васильков и 14 незабудок. Сколькими способами они могут разделить эти цветы?
Решение. Необходимо 10 предметов одного вида, 15 – второго и 14 – третьего разложить в два ящика. Применяя рассуждения, аналогичные приведенным выше, получаем 11×16×15=2460 способов раздела цветов.
Следствие 1. Если все предметы различны (n1=n2=...=nk=1), то их можно разложить 2k способами.
Следствие 2. Если в каждый ящик нужно положить не менее si предметов i-го сорта, то получим формулу: (n1-2s1+1) × (n2-2s2+1) ×...× (nk-2sk+1).
Даны n различных предметов и k ящиков. Надо положить в первый ящик n1 предметов, во второй – n2, ..., в k-ый – nk, где n1+...+nk=n. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике?
Выложим все предметы в один ряд. Это можно сделать n! способами. Первые n1 предметов положим в первый ящик, вторые n2 предмета – во второй ящик, …, k-ые nk предметов – в k-ый ящик. Так как нас не интересует порядок предметов в ящике, то любая перестановка первых n1 предметов не меняет результат раздела. Точно так же его не меняет любая перестановка вторых n2 предметов, ..., k-ых nk предметов. По правилу произведения получаем n1! ×n2!×...×nk! перестановок, не меняющих результата раздела. Таким образом, n! перестановок делятся на группы по n1! ×n2!×...×nk! перестановок в каждой группе, причем перестановки из одной группы приводят к одинаковому распределению предметов. Следовательно, число раздела предметов равно 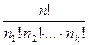 =P(n1,...,nk).
=P(n1,...,nk).
Задача. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?
Решение. Переформулируем задачу: необходимо разложить 28 предметов в 4 ящика по 7 предметов в каждый, причем порядок предметов в ящике не важен. Получаем 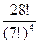 способов распределения костей домино.
способов распределения костей домино.
Можно было рассуждать другим способом. Первый игрок выбирает себе 7 костей из 28, это можно сделать 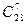 способами. Второму необходимо выбрать 7 костей из оставшихся 21, это можно сделать
способами. Второму необходимо выбрать 7 костей из оставшихся 21, это можно сделать 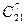 способами. Третьему 7 из 14 –
способами. Третьему 7 из 14 – 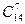 способов. А четвертый заберет оставшиеся. По правилу произведения получаем
способов. А четвертый заберет оставшиеся. По правилу произведения получаем 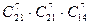 .
.
Даны n различных предметов и k одинаковых ящика. Надо положить в каждый ящик n1 предметов, где n1= 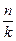 . Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике и все ящики одинаковы?
. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике и все ящики одинаковы?
Задача отличается от предыдущей только тем, что ящики не пронумерованы. Так как k ящиков можно переставить k! способами, то полученный в предыдущей задаче результат необходимо разделить на k!. Всего 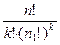 способов распределения.
способов распределения.
Задача. Сколькими различными способами можно разделить 8 книг на 4 бандероли по 2 книги в каждой?
Решение. Если бы интересовал порядок бандеролей, то существовало бы 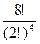 способов распределения книг. Так как не важно, в каком порядке будут отправлены бандероли, то полученное число необходимо поделить на 4!. Итого
способов распределения книг. Так как не важно, в каком порядке будут отправлены бандероли, то полученное число необходимо поделить на 4!. Итого 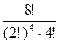 способов разделить 8 книг на 4 бандероли по 2 книги.
способов разделить 8 книг на 4 бандероли по 2 книги.
Сколькими способами можно разложить n одинаковых предметов в k ящиков?
Выложим все предметы в один ряд, добавим к ним k–1 одинаковых разделяющих предмета. Переставим всеми возможными способами n данных одинаковых предметов и k–1 разделяющих. Каждая такая перестановка определяет один из способов распределения. А именно предметы, расположенные до первого разделителя, положим в первый ящик, предметы, расположенные между первым и вторым разделителем, – во второй ящик и так далее, предметы, расположенные после k–1 разделителя, – в k ящик. По формуле перестановок с повторениями число таких перестановок равно P(n, k–1)= 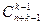 . Значит, всего имеем
. Значит, всего имеем 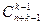 способов разложить n одинаковых предметов в k ящиков.
способов разложить n одинаковых предметов в k ящиков.
Задача. Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут их разделить, если все яблоки считаются одинаковыми (то есть нас интересует, сколько яблок получит каждый, а не какие именно)?
Решение. Добавим два разделяющих предмета, тогда получаем Р(40, 2)=780 способа разделить яблоки.
Следствие 1. Если в каждый ящик надо положить не менее r предметов, то получим: P(n–k×r, k–1) способов.
Следствие 2. Если в каждый ящик надо положить хотя бы один предмет, то r=1, и получим P(n–k, k–1)= 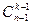 способов распределения.
способов распределения.
Сколько существует способов разложить n различных предметов в k ящиков, если нет никаких ограничений?
Каждый предмет можно положить в любой из k ящиков. Получаем kn способов распределения предметов по ящикам.
Задача. Сколькими способами можно разделить 8 различных пирожных между 5 детьми?
Решение. Необходимо разложить 8 предметов по 5 ящикам. Это можно сделать 58=390 625 способами.
Сколькими способами можно поместить n различных предметов в k ящиков, если не должно быть пустых ящиков?
Данные r ящиков остаются пустыми, если в k–r ящиков предметы кладутся без ограничений. r пустых ящиков можно выбрать Cnk способами. В оставшиеся k–r ящиков предметы можно разложить (k–r)n способами. По формуле включений и исключений число распределений, при которых хотя бы один ящик остается пустым, равно 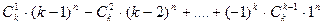 . Тогда количество распределений, при которых ни один ящик не окажется пустым, равно
. Тогда количество распределений, при которых ни один ящик не окажется пустым, равно
kn–( 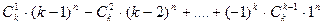 ).
).
Задача. Сколькими способами можно послать по почте 8 различных фотографий, использовав 5 конвертов?
Разбор. Переформулируем задачу: необходимо 8 предметов разложить в 5 ящиков. Посылать пустые конверты не рационально, поэтому накладывается запрет на пустые ящики.
Применяя полученную выше формулу, получаем
58– 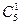 ×48+
×48+ 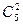 ×38–
×38– 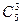 ×28+
×28+ 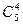 ×18=126 020.
×18=126 020.
Имеется n1 предметов одного сорта, n2 – другого, ... , ns – s-го сорта. Сколькими способами их можно разложить по k ящикам, если не должно быть пустых ящиков?
Применяя рассуждения, аналогичные предыдущей задаче, получим следующую формулу
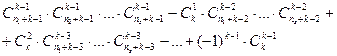 .
.
Задача. Сколькими способами можно разделить 8 яблок, 10 груш и 7 апельсинов между 4 детьми, если каждый должен получить хотя бы один фрукт?
Решение. Требуется 8 предметов одного сорта, 10 второго и 7 третьего разложить в 4 ящика так, чтобы ни один ящик не оказался пустым. По предыдущей формуле получаем
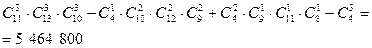 способов такого распределения.
способов такого распределения.
Сколькими способами можно распределить n различных предметов по k различным ящикам с учетом порядка расположения предметов в ящиках, причем все n предметов должны быть использованы?
Добавим к n предметам k–1 одинаковых разделяющих предмета. Рассмотрим все возможные перестановки из n различных предметов и k–1 одинаковых. Каждая такая перестановка определяет один из способов распределения. Всего таких перестановок 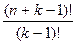 . Значит, n различных предметов можно разложить в k ящиков, с учетом расположения их в ящиках,
. Значит, n различных предметов можно разложить в k ящиков, с учетом расположения их в ящиках, 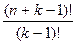 =
= 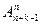 способами.
способами.
К тому же результату можно было прийти и другим путем. Переставим всеми возможными способами данные n предметов (n! способов). Теперь считаем предметы неразличимыми, их можно разложить в k ящиков Р(n, k–1) способами. Получаем n!∙Р(n, k–1)= 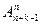 способов распределения этих вещей по k различным ящикам с учетом порядка их расположения в ящиках.
способов распределения этих вещей по k различным ящикам с учетом порядка их расположения в ящиках.
Задача. Имеются 6 различных сигнальных флагов и 3 мачты, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке вывешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
Решение. Имеем 6 предметов, которые необходимо разложить в 3 ящика, причем порядок предметов в ящике важен. Это можно сделать 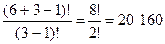 способами.
способами.
Следствие. Если не должно быть пустых ящиков, то выберем k предметов и разложим по одному в каждый ящик. Это можно сделать 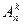 способами. Оставшиеся n–k предметов разложим в k–1 ящик, причем теперь некоторые ящики могут оказаться пустыми. Это распределение можно осуществить
способами. Оставшиеся n–k предметов разложим в k–1 ящик, причем теперь некоторые ящики могут оказаться пустыми. Это распределение можно осуществить 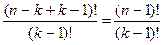 способами. Всего имеем
способами. Всего имеем 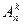
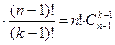 способов распределения.
способов распределения.
Сколькими способами можно распределить n различных предметов по k различным ящикам с учетом порядка расположения предметов в ящиках, причем не все n предметов могут быть использованы и некоторые ящики могут оказаться пустыми?
