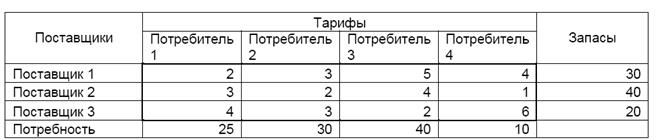
Анализ результатов решения

Полученное решение оптимально, но может быть не единственным. Для поиска других возможных решений можно воспользоваться отчетами, создаваемыми программой.

Отчет по результатам

Отчет по устойчивости – содержит две таблицы.

· В таблице «Изменяемые ячейки» кроме результирующих значений этих ячеек приведен нормированный градиент, указывающий, на сколько изменится ЦФ, если значений в данной изменяемой ячейке увеличится на единицу. Для транспортной задачи нормированный градиент равен разности тарифа и косвенного тарифа для данной ячейки. Эта разность называется оценкой свободных (т.е. с нулевой перевозкой) ячеек. Косвенный тариф определяется как сумма потенциалов свободных ячеек. Если все оценки свободных ячеек ≥ 0, то такой план улучшить нельзя, поскольку увеличение значения в любой ячейке приведет к увеличению ЦФ. Наличие оценки ≤ 0 в какой-то свободной ячейке укажет на неоптимальность плана, т.к. размещение в ней ненулевого значения перевозки уменьшит ЦФ. Чем больше значение оценки, тем менее перспективна данная ячейка для включения ее в план перевозок.

· В таблице «Ограничения» приведен множитель Лагранжа, который равен отношению прироста ЦФ к изменению ограничения на единицу. Иногда его называют «ценность ресурса», поскольку он указывает на чувствительность ЦФ к изменению данного ресурса.

Отчет по пределам – содержит две таблицы. В первой указано значение ЦФ, а во второй приведен список влияющих ячеек, их значений, а также нижних и верхних пределов. Для транспортной задачи с закрытой моделью верхние и нижние пределы совпадают.

Транспортная задача с открытой моделью

В моделях с открытой моделью запасы поставщиков не равны потребностям потребителей.

Открытая модель-1

Запасы поставщиков больше потребностей.

1. Откройте Лист Excel с закрытой моделью. Удалите из плана доставки полученные результаты. Измените данные в столбце «Запасы на складе», согласно Таблице 6.

Таблица 6

Исходные данные – открытая модель-1

Изменится общая сумма запасов на складе (100) и в ячейке G15 появится сообщение «не совпадает».

2. Эта ситуация приведет к тому, что исчерпаны будут не все запасы, Измените одно из ограничений, как на Рис.40, где неравенство $F$11:$F$13 <= $G$11:$G$13 означает условие неполного распределения запасов.

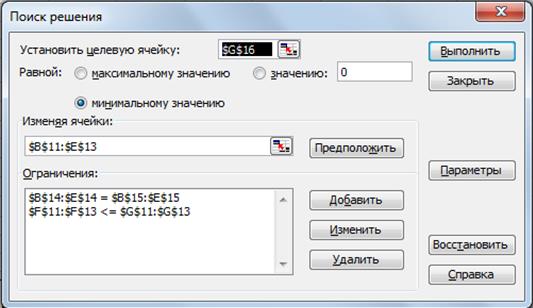
Рис. 40. Заполнение диалогового окна ПОИСК РЕШЕНИЯ

3. Сохраните результат выполнения поиска решения при новых условиях в виде сценария с именем «Открытая_М-1».

4. Результат решения – на Рис.41.

Рис. 41. Фрагмент рабочего листа с результатами поиска решения

Открытая модель-2

Запасы поставщиков меньше потребностей.

1. Откройте Лист Excel с открытой моделью первого варианта. Удалите из плана доставки полученные результаты. Измените исходные данные согласно Таблице 7.

Таблица 7

Исходные данные – Открытая модель-2

Изменится общая сумма запасов на складе (90) и потребностей (105). Значение ячейки G15 − «не совпадает».

2. Выполните поиск решения в новых условиях, изменив ограничения;

3. Вид ограничений показан в окне ПОИСКА РЕШЕНИЯ на Рис.42., где выражение $B$14:$E$14 <= $B$15:$E$15 означает условие неполного удовлетворения потребностей.

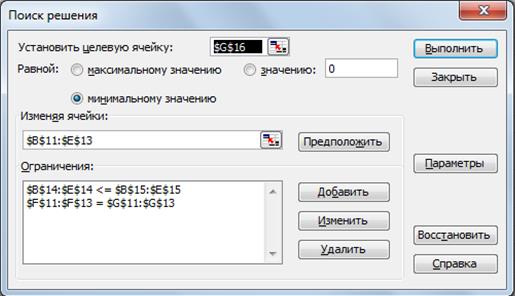
Рис. 42. Изменение ограничений поиска решения

4. Результат решения – на Рис. 43. – сохраните его в виде сценария с именем «Открытая_М-2».

Рис. 43. Фрагмент рабочего листа с результатами поиска решения.

5. Сохраните задачу в виде книги Excel с именем «Транспортная-задача.xls».

Задача о назначениях

Задача о назначениях – частный случай транспортной задачи. Такая задача решается при определения маршрута передвижения людей, автомашин; при распределении людей на работы, должности; при распределении групп по аудиториям и т.д.