Принципы и методы построения имитационных моделей
Процесс функционирования сложной системы можно рассматривать как смену ее состояний, описываемых ее фазовыми переменными
Z1(t), Z2(t), … Zn(t) в n – мерном пространстве.
Задачей имитационного моделирования является получение траектории движения рассматриваемой системы в n – мерном пространстве (Z1, Z2, … Zn), а также вычисление некоторых показателей, зависящих от выходных сигналов системы и характеризующих ее свойства.
В данном случае “движение” системы понимается в общем смысле – как любое изменение, происходящее в ней.
Известны два принципа построения модели процесса функционирования систем:
2.3.1. Принцип  Δt. Рассмотрим этот принцип сначала для детерминированных систем. Предположим, что начальное состояние системы соответствует значениям Z1(t0), Z2(t0), … Zn(t0). Принцип
Δt. Рассмотрим этот принцип сначала для детерминированных систем. Предположим, что начальное состояние системы соответствует значениям Z1(t0), Z2(t0), … Zn(t0). Принцип  t предполагает преобразование модели системы к такому виду, чтобы значения Z1, Z2, … Zn в момент времени t1= t0
t предполагает преобразование модели системы к такому виду, чтобы значения Z1, Z2, … Zn в момент времени t1= t0  t можно было вычислить через начальные значения, а в момент t2= t1+
t можно было вычислить через начальные значения, а в момент t2= t1+  t χчерез значения на предшествующем шаге и так для каждого i-ого шага (
t χчерез значения на предшествующем шаге и так для каждого i-ого шага (  t=const, i=1
t=const, i=1 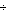 M).
M).
Для систем, где случайность является определяющим фактором, принцип  t заключается в следующем:
t заключается в следующем:
1. Определяется условное распределение вероятности на первом шаге (t1= t0+  t) для случайного вектора,обозначим его (Z1, Z2, … Zn). Условие состоит в том, что начальное состояние системы соответствует точке траектории
t) для случайного вектора,обозначим его (Z1, Z2, … Zn). Условие состоит в том, что начальное состояние системы соответствует точке траектории 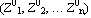 .
.
2. Вычисляются значения координат точки траектории движения системы (t1= t0+  t), к ак значения координат случайного вектора, заданного распределением, найденным на предыдущем шаге.
t), к ак значения координат случайного вектора, заданного распределением, найденным на предыдущем шаге.
3. Отыскиваются условное распределение вектора 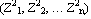 на втором шаге (t2= t1+
на втором шаге (t2= t1+  t), при условии получения соответствующих значений
t), при условии получения соответствующих значений 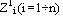 на первом шаге и т.д., пока ti= t0+ i
на первом шаге и т.д., пока ti= t0+ i  t не примет значения (tМ= t0+ М
t не примет значения (tМ= t0+ М  t).
t).
Принцип  t является универсальным, применим для широкого класса систем. Его недостатком является неэкономичность с точки зрения затрат машинного времени.
t является универсальным, применим для широкого класса систем. Его недостатком является неэкономичность с точки зрения затрат машинного времени.
2.3.2. Принцип особых состояний (принцип 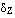 ). При рассмотрении некоторых видов систем можно выделить два вида состояний:
). При рассмотрении некоторых видов систем можно выделить два вида состояний:
· обычное, в котором система находится большую часть времени, при этом Zi(t), (i=1 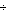 n) изменяются плавно.
n) изменяются плавно.
· особое, характерное для системы в некоторые моменты времени, причем состояние системы изменяется в эти моменты скачком.
Принцип особых состояний отличается от принципа  t тем, что шагпо времени в этом случае не постоянен, является величиной случайной и вычисляется в соответствии с информацией о предыдущем особом состоянии.
t тем, что шагпо времени в этом случае не постоянен, является величиной случайной и вычисляется в соответствии с информацией о предыдущем особом состоянии.
Примерами систем, имеющих особые состояния, являются системы массового обслуживания. Особые состояния появляются в моменты поступления заявок, в моменты освобождения каналов и т.д.
Для таких систем применение принципа  t является нерациональным, так как при этом возможны пропуски особых состояний и необходимы методы их обнаружения.
t является нерациональным, так как при этом возможны пропуски особых состояний и необходимы методы их обнаружения.
В практике использования имитационного моделирования описанные выше принципы при необходимости комбинируют.
2.3.3. Пример применения принципа  t.
t.
На рис. 2.2. приведена аналоговая схема дифференцирующего фильтра.
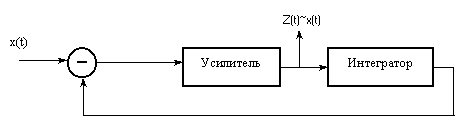
Рис. 2.2.
Процесс, происходящий в фильтре, описывается дифференциальным уравнением:

В уравнении:
K- коэффициент усиления,
х(t) – входной сигнал.
Доказано, что 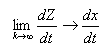
Преобразуем математическую модель фильтра (1) к виду, позволяющему применить принцип  t. В простейшем случае достаточно уравнение (1) аппроксимировать конечно-разностным уравнением:
t. В простейшем случае достаточно уравнение (1) аппроксимировать конечно-разностным уравнением:
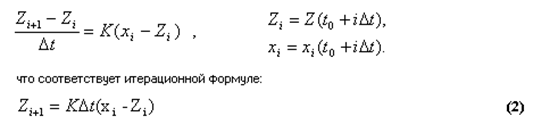
Задав начальное условие Z(t0)=Z0 можно построить траекторию процесса, происходящего в фильтре, с целью получения текущего значения производной любой детерминированной функции x(t), подаваемой на вход.
2.3.4. Пример применения принципа особых состояний
Рассмотрим магазин мелких подарков “Виртуальный”. В магазине работает один продавец. Требуется имитировать работу магазина с целью изучения перспектив его развития. Из предварительного обследования получена информация, что интервал времени между двумя последовательными приходами покупателей в магазине имеет равномерный закон распределения в интервале (1,10). Время обслуживания покупателей в магазине также распределено равномерно в интервале (1,6).
2.3.5. Основные методы имитационного моделирования
Основными методами имитационного моделирования являются: аналитический метод, метод статического моделирования и комбинированный метод (аналитико-статистический) метод.
Аналитический метод применяется для имитации процессов в основном для малых и простых систем, где отсутствует фактор случайности. Например, когда процесс их функционирования описан дифференциальными или интегродифференциальными уравнениями. Метод назван условно, так как он объединяет возможности имитации процесса, модель которого получена в виде аналитически замкнутого решения, или решения полученного методами вычислительной математики.
Метод статистического моделирования первоначально развивался как метод статистических испытаний (Монте-Карло). Это – численный метод, состоящий в получении оценок вероятностных характеристик, совпадающих с решением аналитических задач (например, с решением уравнений и вычислением определенного интеграла). В последствии этот метод стал применяться для имитации процессов, происходящих в системах, внутри которых есть источник случайности или которые подвержены случайным воздействиям. Он получил название метода статистического моделирования. В параграфах 2-5 данного раздела излагается суть этого метода.
Комбинированный метод (аналитико-статистический) позволяет объединить достоинства аналитического и статистического методов моделирования. Он применяется в случае разработки модели, состоящей из различных модулей, представляющих набор как статистических так и аналитических моделей, которые взаимодействуют как единое целое. Причем в набор модулей могут входить не только модули соответствующие динамическим моделям, но и модули соответствующие статическим математическим моделям.
Вопросы для самопроверки
1. Можно ли все то, что решается с помощью ЭВМ назвать имитационным моделированием? Если – нет, то можно ли указать четкую границу между имитационным моделированием и моделированием с помощью ЭВМ?
2. Объясните, почему метод имитационного моделирования становиться одним из основных инструментов исследования технологических, социально-экономических, биологических и других видов процессов?
3. Объясните разницу между принципами  t и
t и 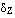 . Приведите примеры.
. Приведите примеры.
4. В чем вы видите трудности разработки имитационных моделей больших систем? Перечислите их и прокомментируйте.
5. Имеется квадратная труба с квадратным отверстием внутри нее. По трубе течет горячая жидкость. Труба помещена в ледяную ванну. Распределение температуры в теле трубы в ее сечении удовлетворяет уравнению в частных производных
Uxx+Uyy=0, (3)
а распределение температур на границе трубы задано начальными условиями. Разностные уравнения, соответствующие (3) имеют вид:
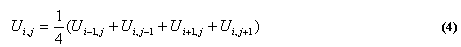
Задачу можно решить, задавая начальные условия и задавая i и j в соответствии с необходимым количеством разбиений интервалов в направлениях по координатным осям x и y, при реализации модели (4) с помощью ЭВМ, можно ли считать данную модель имитационной? Дайте ответ на этот вопрос, если вместо (3) имеется уравнение Uxx+Uyy=aUt, учитывающее переходной процесс. А если учитывать понижение температуры вдоль трубы и задачу рассматривать как трехмерную?
6. К какому классу относятся системы, для которых применим метод имитационного моделирования?
7. Можно ли отнести модели всех видов процессов, исследуемых с помощью ЭВМ к имитационным?
Упражнения
1. Задано уравнение 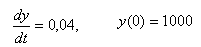
а) Преобразовать уравнение к виду, позволяющему применить принцип  t;
t;
б) Найдите решение уравнения, то есть математическую модель процесса y(t) с шагом h=1, 0.5, 0.25.
в) Сравните результаты с точным решением уравнения 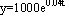 , сделайте выводы;
, сделайте выводы;
г) Проинтегрируйте пункты а) – в) в терминах банковских операций.
2. Задана модель простейшего цифрового фильтра
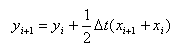
Здесь х0, х1 . . . входной процесс, заданный дискретными значениями через шаг  t=const, y0, y1 – соответственно выходной процесс. Составьте программу имитации работы фильтра. Постройте график амплитудно-частотной характеристики. Какой вывод можно сделать? Какой принцип и метод построения ИМ Вами применен?
t=const, y0, y1 – соответственно выходной процесс. Составьте программу имитации работы фильтра. Постройте график амплитудно-частотной характеристики. Какой вывод можно сделать? Какой принцип и метод построения ИМ Вами применен?
3. Степень радиоактивности пропорциональна количеству остающегося радиоактивного вещества. Процесс уменьшения радиоактивности с течением времени может быть описан математической моделью
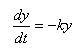
Предположим, что k = 0.01, y0 = 100 (г. радиоактивного вещества).
Имитировать процесс распада вещества во времени, построить график процесса, определить сколько вещества останется в момент t=100. Применить принцип  t. Получите решение одним из методов вычислительной математики и в аналитически замкнутой форме.
t. Получите решение одним из методов вычислительной математики и в аналитически замкнутой форме.
4. Закон распределения интервала времени Т между прибытиями автобуса на остановку распределены по равномерному закону (5 мин., 10 мин.). Имитировать процесс прибытия автобусов в течении часа на ЭВМ.
5. В информационную систему поступают требования на выполнение заявок. Интервалы между требованиями Т распределены нормально. Использовав программный датчик и положив М[Т]=2, и дисперсию D[T]=1, имитировать процесс поступления требований. Положить количество требований равным 100 и получить оценки М[T] и D[T], сравнив их с теоретическими оценками.
6. Проанализируйте процесс решения упражнения 5 и составьте его этапы структурной имитационной модели (рис. 2.1.)
