Какое положение равновесия называется устойчивым, безразличным и неустойчивым?

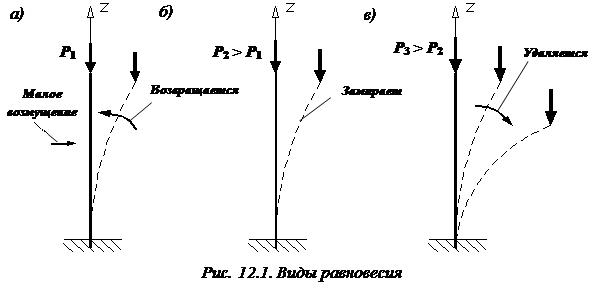
Рассмотрим длинный стержень (рис. 12.1), нагруженный осевой сжимающей силой P. Пока нагрузка на стержень невелика 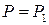, его прямолинейное положение равновесия является устойчивым, поскольку,получив малое боковое отклонение от вертикали, он под действием упругих сил быстро возвратится в первоначальное прямолинейное положение равновесия (см. рис. 12.1, а), после исчезновения причин, вызвавших это отклонение.

По мере увеличения нагрузки стержень это делает все медленнее и медленнее. И наконец, при некоторой нагрузке 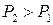(см. рис. 12.1, б) он замрет в близком, изогнутом положении равновесия даже после исчезновения причин, вызвавших это отклонение.

В этом случае говорят, что первоначальное прямолинейное положение равновесия является безразличным, поскольку наряду с прямолинейной формой равновесия стержня возможна и близкая к ней, изогнутая форма равновесия.

При дальнейшем, даже весьма малом, увеличении нагрузки 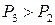прямолинейное положение равновесия становится неустойчивым. Слегка отклоненный от вертикали стержень будет изгибаться и после исчезновения причин, вызвавших это отклонение, пока не займет положение равновесия, которому соответствуют уже значительные прогибы (см. рис. 12.1, в).

12.3. Что называется потерей устойчивости стержня?

Переход стержня из устойчивого в неустойчивое положение равновесия называется потерей устойчивости. На практике потеря устойчивости стержня сопровождается качественным изменением вида деформации: деформация сжатия внезапнопереходит в деформацию изгиба. Очень часто такой внезапный переход от прямолинейной формы равновесия к криволинейной называется выпучиванием стержня.

12.4. Какая нагрузка называется критической?

Нагрузка, превышение которой вызывает потерю устойчивости прямолинейной формы равновесия стержня, называется критической. Она обозначается 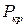. Из изложенного выше примера следует, что .

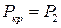Можно утверждать, что потеря устойчивости равносильна разрушению стержня. При 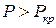прямолинейная форма равновесия становится неустойчивой, стержень изогнется и это, в свою очередь, приведет к практически неограниченному росту напряжений.

12.5. Что называется формой потери устойчивости стержня?

При потере устойчивости прямолинейная ось стержня искривляется. Конфигурация изогнутой оси стержня называется формой потери устойчивости. Форма потери устойчивости зависит от условий закрепления стержня и места приложения сжимающей нагрузки по его длине.

12.6. Какая нагрузка называется эйлеровой?

В 1744 г. Эйлер впервые получил формулу для определения теоретической нагрузки, при которой происходит потеря устойчивости стержня. Эту нагрузку, как правило, называют эйлеровой. Она равна:

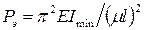, (12.1)

где Е – модуль Юнга; 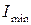– минимальный главный центральный момент инерции поперечного сечения (очевидно, что при потере устойчивости изгиб стержня произойдет именно в плоскости наименьшей жесткости, то есть поперечные сечения стержня будут поворачиваться вокруг той из главных осей, относительно которой момент инерции минимален); 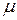– коэффициент приведения длины стержня, зависящий от формы потери устойчивости; l – длина стержня. Произведение 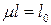называется приведенной, или свободной, длиной стержня.

12.7. Почему 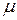называется коэффициентом приведения длины, а произведение 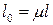– приведенной длиной стержня?

Для шарнирно опертого стержня, сжатого по концам, Эйлером была получена следующая формула

.

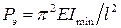В этом случае 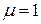. Форма потери устойчивости такого стержня представляет собой одну полуволну синусоиды (рис. 12.2, а).И этот случай принято считать основным случаем потери устойчивости.

Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по его торцам) легко могут быть приведены к основному случаю путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.

Рассмотрим еще два наиболее часто встречающихся случая закрепления концов стержня.

1) Стержень с жестко защемленным одним и совершенно свободным другим концом. При потере устойчивости он изогнется, как показано на рис. 12.2, б. Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Следовательно, в этом случае приведенная длина равна 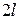(полуволна синусоиды имеет длину 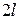), а эйлерова сила в

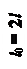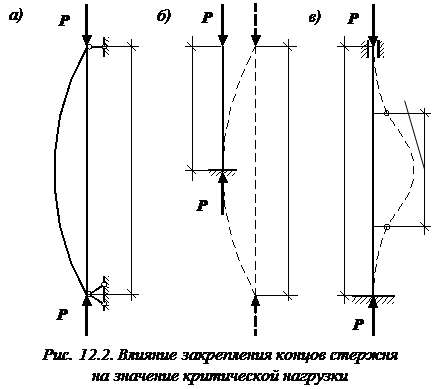четыре раза меньше, чем для основного случая:

.

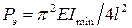2) Оба конца стержня жестко защемлены. В этом случае форма потери устойчивости такова, что одна полуволна синусоиды занимает половину длины стержня (рис. 12.2, в). Поэтому приведенная длина стержня равна 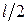( 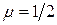), а эйлерова нагрузка

,

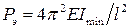то есть в четыре раза больше, чем для основного случая.

12.8. Всегда ли справедлива формула Эйлера? Иными словами, всегда ли значение эйлеровой нагрузки совпадает со значением критической нагрузки?

Отметим, что критической 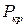принято называть истинную, а эйлеровой 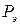– теоретическую нагрузку, при которой происходит потеря устойчивости стержня.

Формула Эйлера получена при предположении, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности 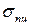, то есть

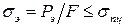. (12.2)

Об этом, в частности, говорит присутствие в формуле (12.1) модуля Юнга Е, который свидетельствует о том, чтовплоть до момента потери устойчивости выполнялся закон Гука.

Поэтому, если потеря устойчивости происходит при напряжении меньшем, чем 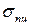, то .

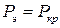Для стержней, теряющих устойчивость при напряжении, превышающем предел пропорциональности 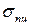, использование формулы Эйлера не только принципиально неправильно, но и крайне опасно по своим последствиям, поскольку критическая нагрузка (истинная нагрузка, при которой происходит потеря устойчивости) меньше эйлеровой: .

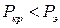12.9. Каковы пределы применимости формулы Эйлера?

Пределы ее применимости можно легко установить, предварительно введя понятие гибкости стержня, предложенное Феликсом Станиславовичем Ясинским (1856 – 1899 гг.).

Определим эйлеровы напряжения, исходя из формулы Эйлера (12.1):

.

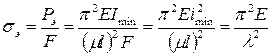Здесь 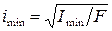– геометрическая характеристика поперечного сечения, называемая минимальным радиусом инерции, которая измеряется (см. беседу 4) в сантиметрах; 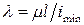– безразмерная геометрическая характеристика, называемая гибкостью сжатого стержня.

С учетом формулы (12.2), находим, что

.

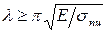Величину, стоящую в правой части этого неравенства, обозначим 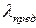и назовем предельной гибкостью. Тогда

.

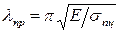В отличие от гибкости стержня, представляющей собой его геометрическую характеристику, предельная гибкость зависит только от физико-механических свойств материала и не зависит от его размеров.

Предельная гибкость – постоянная для данного материала величина. Например, для стали марки Ст. 3 .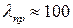

Используя понятие предельной гибкости, пределы применимости формулы Эйлера можно представить в виде:

.

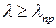Таким образом, формула Эйлера дает истинное значение нагрузки, при которой происходит потеря устойчивости стержня, только в том случае, когда гибкость рассчитываемого стержня больше или равна предельной гибкости для материала, из которого он изготовлен.

12.10. По какой формуле определяется критическая нагрузка для стержней малой и средней гибкости (при )?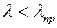

В случае, когда формула Эйлера неприменима, критическая нагрузка определяется по эмпирической формуле, предложенной Ясинским, на основе опытов, проведенных рядом исследователей. Она имеет вид:

,

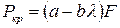где а и b – коэффициенты, зависящие от свойств материала и измеряющиеся в единицах напряжения. Например, для стали марки Ст. 3 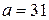кН/см², 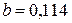кН/см²; для дерева 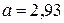кН/см², 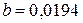кН/см².

Для очень коротких стержней (при некоторой гибкости, обозначаемой 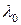) критическое напряжение, то есть напряжение, при котором происходит потеря устойчивости стержня, может оказаться равным предельному напряжению (при сжатии: пределу текучести для пластичных материалов или пределу прочности для хрупких). Тогда, при :

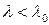· для пластичных материалов

,

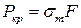· для хрупких

.

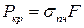12.11. Можно ли увеличить критическую нагрузку стержня, заменив, например, одну марку стали на другую, имеющую больший предел текучести?

Для стержней с одинаковыми геометрическими размерами и с одинаковыми условиями закрепления концов замена одной марки стали на другую может изменить, а может и не изменить критическую нагрузку.

Критическая нагрузка не изменится, если она определяется по формуле Эйлера (при 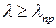), поскольку входящий в эту формулу модуль Юнга практически не зависит ни от химического состава стали, ни от ее термической обработки (для всех марок стали 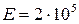МПа).

Однако для стержней средней гибкости (при 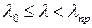), а также для коротких стержней (при 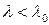) такая замена марки стали приведет к увеличению критической нагрузки. В первом случае это объясняется тем, что эмпирические коэффициенты а и b в формуле Ясинского существенно зависят от марки стали, а во втором стержень, по существу, рассчитывается не на устойчивость, а на прочность.

12.12. Как осуществляется расчет центрально сжатого стержня на устойчивость и что такое коэффициент уменьшения основного допускаемого напряжения (коэффициент продольного изгиба)?

При назначении размеров длинного сжатого стержня, в первую очередь, приходится заботиться о том, чтобы он в процессе эксплуатации не потерял устойчивость прямолинейной формы равновесия. Поэтому напряжения в сжатом стержне не должны превышать критических напряжений:

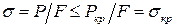. (12.3)

Исследования показали, что незначительные местные ослабления стержня (например, заклепочные отверстия) не оказывают существенного влияния на значение критической нагрузки, поэтому в формуле (12.3) берется вся площадь поперечного сечения (площадь брутто).

Условие прочности при сжатии, как известно, имеет вид:

.

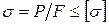Расчет сжатого стержня на устойчивость можно по форме привести к расчету на простое сжатие. Однако при этом необходимо учесть, что длинный стержень (стержень большой гибкости) может потерять устойчивость, то есть исчерпает несущую способность, при меньшем напряжении, чем допускаемое напряжение 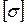. Поэтому условие устойчивости сжатого стержня можно представить в виде:

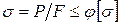, (12.4)

где 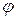– коэффициент, называемый коэффициентом уменьшения основного допускаемого напряжения или коэффициентом продольного изгиба. Очевидно, что этот коэффициент зависит от материала стержня и от его гибкости 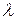и изменяется в пределах от 0 (при 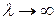) до 1 (при ).

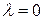Этот метод расчета очень удобен в том смысле, что он не связан с пределами применимости формулы Эйлера и может быть использован практически при всех значениях гибкости.

Заметим, что проектировочный расчет по формуле (12.4), связанный с подбором размеров поперечного сечения стержня

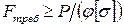, (12.5)

приходится осуществлять методом последовательных приближений. Это обусловлено тем, что площадь поперечного сечения стержня в неявном виде входит и в правую часть выражения (12.5), поскольку коэффициент продольного изгиба 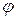зависит от гибкости стержня 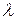, а последняя, в свою очередь, от радиуса инерции .

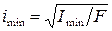12.13. Какой стержень называется равноустойчивым?

Мы уже отмечали, что если стержень одинаково закреплен в обеих главных плоскостях инерции, то при вычислении критической нагрузки в расчет необходимо вводить наименьший из главных моментов инерции.

Поэтому рациональным будет такое поперечное сечение стержня, для которого главные моменты инерции равны между собой: 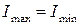. Такой стержень и называется равноустойчивым.

Так, например, если поперечное сечение стержня состоит из двух рядом расположенных двутавров, то 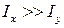. Раздвигая двутавры, мы будем увеличивать момент инерции поперечного сечения 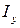. Для того чтобы такой стержень стал равноустойчивым,расстояние между центрами тяжести двутавров, так называемая раздвижка, обозначаемая далее буквой a,должно быть определено из условия, что .

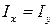Если для одного двутавра моменты инерции обозначить 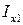и 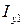(причем 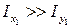), а площадь поперечного сечения – 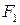, то для определения раздвижки можно записать следующее равенство:

.

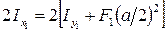Осюда раздвижка двутавров равна

.

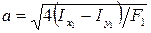ЗАДАЧИ ДИНАМИКИ

Вся теория, изложенная в предыдущих наших беседах, основывалась на статическом действии внешних нагрузок. Мы полагали, что нагрузки, прикладываемые к стержням, возрастают от нуля до своего конечного значения настолько медленно, что ускорениями частиц тела, возникающими при его деформировании, можно пренебрегать. Поэтому мы считали, что в каждый момент времени внешние и внутренние силы взаимно уравновешены.

Однако в процессе эксплуатации конструкции приходится иметь дело и с нагрузками, которые могут достаточно быстро менять как свое значение, так и положение (последний случай, например, имеет место в случае движущегося по мосту поезда). Такая нагрузка называется динамической. Она вызывает весьма большие ускорения частиц тела при его деформировании, и поэтому в расчете, помимо внешних и внутренних сил, необходимо учитывать и так называемые силы инерции.

13.1. Что понимается под силой инерции в сопротивлении материалов?

Рассмотрим следующий пример. К грузу массой m привяжем веревку. Другой конец веревки будем удерживать в руке. Начнем вращать массу в горизонтальной плоскости с постоянной угловой скоростью. Будем пренебрегать весом груза. Тогда на массу будет действовать только одна сила – сила натяжения веревки, направленная от груза к руке (так называемая центростремительная сила). Эта сила выводит массу из присущего ей, по свойству инерции, состояния покоя или равномерного и прямолинейного движения и сообщает массе центростремительное ускорение. Согласно третьему закону Ньютона, масса противодействует этой силе. Это противодействие со стороны движущейся с ускорением массы приложено к веревке. Оно ее растягивает с силой, которую и называют силой инерции.

Эту силу инерции, реально действующую со стороны движущейся массы на упругую связь (в нашем примере – на веревку), необходимо отличать от фиктивной силы, которую в теоретической механике, согласно принципу французского ученого Жан де Рона Д’Аламбера (d’Alembert, 1717 – 1783 гг.), условно прикладывают к самой движущейся массе и также называют силой инерции.

Таким образом, в сопротивлении материалов, говоря о силе инерции, мы будем иметь в виду реальную силу, которая представляет собой действие (или, точнее, противодействие), оказываемое движущейся с ускорением массы на упругую связь. Сила инерции, как и внешняя нагрузка, деформирует связь, вызывает в ней внутренние усилия и может привести к разрушению связи.

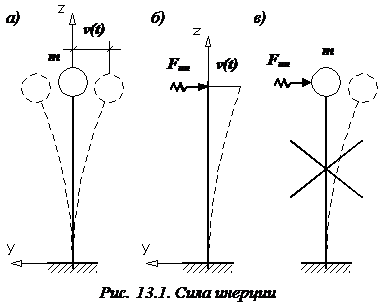
Проиллюстрируем сказанное и на следующем примере. Пусть груз массой m, находящийся на консоли невесомой балки, совершает свободные колебания (рис. 13.1, а).

Отбросим массу(рис. 13.1, б) и действие движущейся массы на невесомую балку (иногда называемую безмассовым упругим скелетом) заменим силой инерции 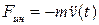, где 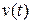– прогиб балкив точке расположения массы, а точками обозначена вторая производная от прогиба по времени t.

Напомним, что обозначение производной по времени точкой было предложено английским ученым Исааком Ньютоном (Newton, 1642 – 1727 гг.)

Заметим, что ошибочно прикладывать реальную силу инерции к самой движущейся массе(рис. 13.1 в), как это делается в некоторых учебниках по сопротивлению материалов.

Понятие «сила инерции» в 1803 г. ввел французский ученый Лазар Никола Маргерит Карно (Carnot, 1753 – 1823 гг.).

13.2. Как вычисляются напряжения в тросе при ускоренном поднятии (опускании) груза?

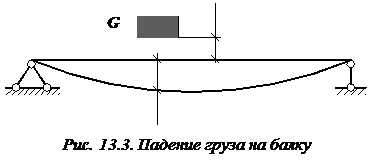
Пусть груз массой m поднимают на тросе с ускорением 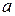(рис. 13.2, а). И пусть погонная масса троса (масса троса, приходящаяся на единицу его длины) равна .

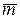Определим продольное динамическое усилие 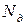, возникающее в некотором сечении троса, находящемся на расстоянии 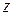от груза.

Отбросим движущиеся массы груза и участка троса длиной z и заменим их действие на безмассовый упругий скелет тросасилой их веса

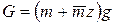
и суммарной силой инерции

,

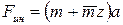направленной в сторону, противоположную ускорению 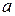(рис. 13.2, б).

Из уравнения равновесия находим:

.

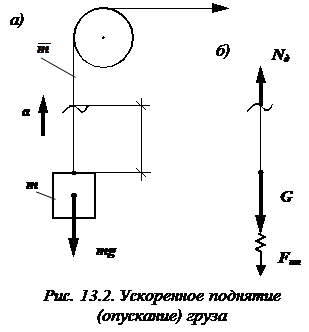
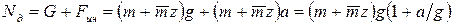Если бы груз был неподвижен, то

.

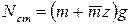Тогда, окончательно получим:

.

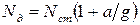Эффект действия динамической нагрузки на практике, как правило, оценивается коэффициентом динамичности, представляющим собой отношение динамического усилия (перемещения) к статическому усилию (перемещению):

.

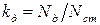В рассматриваемом нами случае он оказывается равным:

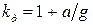. (13.1)

Таким образом, при поднятии груза с ускорением 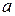внутреннее динамическое продольное усилие в тросе 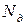может в несколько раз превысить статическое усилие 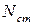. Так, например, в скоростных лифтах, в которых большая скорость подъема может быть достигнута только благодаря большим ускорениям, динамическое усилие и соответственно динамическое напряжение в тросе бывает очень большим.

Если груз опускается с ускорением 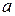, то в формуле (13.1) перед вторым слагаемым нужно поставить знак «минус». Заметим, что при свободном падении груза, когда 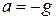, динамическое усилие в тросе будет равно нулю.

13.3. Какое воздействие на стержень называется ударом?

Под ударом понимается взаимодействие движущихся тел, которое происходит в результате их соприкосновения. Удар сопровождается резким изменением скоростей частиц этих тел за весьма малый промежуток времени, при этом сила удара достигает, как правило, очень большого значения.

В качестве примера можно привести действие кузнечного молота на кусок металла, удар падающего груза при забивке свай, воздействие колеса вагона на рельс при перекатывании через стык и т. п.

13.4. Какие основные допущения принимаются при расчете на удар?

За исключительно короткий промежуток времени, в течение которого совершается удар, очень трудно произвести какие-либо измерения, связанные с определением силы удара. Поэтому обычно производится условный расчет на удар, по которому определяются внутренние силы и перемещения, возникающие в стержне после удара. При этом сначала определяется наибольшее динамическое перемещение точки стержня, по которой наносится удар, а затем и напряженное состояние самого стержня.

Методика расчета на удар в сопротивлении материалов основывается на следующих основных допущениях:

1) деформация стержня, вызванная ударной нагрузкой, описывается законом Гука, а сам стержень является линейно деформируемой системой, при этом модуль Юнга имеет такое же значение, как и при статическом нагружении стержня;

2) работа, совершаемая падающим грузом, полностью переходит в потенциальную энергию деформации стержня;

3) масса стержня, воспринимающего удар, пренебрежимо мала по сравнению с массой падающего груза;

4) удар считается неупругим, то есть после соприкосновения падающего груза со стержнем он не отскакивает и продолжает движение вместе со стержнем при его деформации.

13.5. Чему равен коэффициент динамичности при поперечном ударе?

Рассмотрим удар груза весом G, падающегос высоты h на некоторую упругую систему, например балку (рис. 13.3).

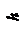
Обозначим 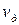– динамический прогиб балки в месте падения груза.

Работа, совершаемая падающим грузом, равна:

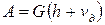. (13.2)

Согласно принятому второму допущению, работа полностью переходит в потенциальную энергию деформации балки V. По теореме Клапейрона (см. далее беседу 15) потенциальная энергия деформации равна половине произведения некоторой динамической силы 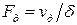на соответствующее ей динамическое перемещение :

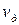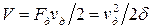. (13.3)

Приравнивая выражения (13.2) и (13.3), а также учитывая, что статический прогиб балки в месте падения груза G, вызванный его статическим приложением, равен 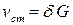, после несложных преобразований получим следующее квадратное уравнение относительно динамического прогиба балки:

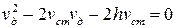. (13.4)

Отсюда

.

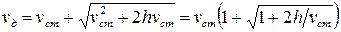Легко убедиться, что второй корень квадратного уравнения (13.4) имеет отрицательное значение 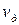, и поэтому он нас не интересует.

Динамический прогиб балки в месте падения груза можно представить в виде:

,

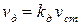где 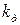– коэффициент динамичности.

Тогда

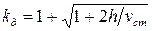. (13.5)

Принятое нами допущение о линейной зависимости между внешней силой и перемещением позволяет сделать вывод о том, что динамические напряжения в балке от действия ударной нагрузки во столько же раз больше напряжений, которые возникли бы в ней при статическом приложении такой же нагрузки, во сколько раз динамический прогиб больше статического, поэтому:

.

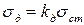В частном случае, когда высота падения 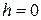, то есть в случае внезапного приложения нагрузки, .

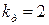Из формулы (13.5) следует, что для уменьшения коэффициента динамичности необходимо увеличить 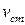. Поэтому для смягчения удара применяют пружинные и резиновые прокладки, допускающие большие деформации.