Задания на контрольную работу
МАТЕМАТИКА
Часть первая
Учебно-методическое пособие по изучению дисциплины и выполнению контрольных работ для студентов первого курса заочной формы обучения для направлений подготовки бакалавров 21.03.01(131000). 13.03.02(140400),
Краснодар
Составители: канд. физ.-мат. наук, доц. И.В.Терещенко, канд. физ.-мат. наук, доц. А.В. Братчиков, ассист. Л.В. Егорова
УДК 517
Математика. Часть первая. Учебно – метод. пос. по изучению дисциплины и выполнению контрольных работ для студентов первого курса заочной формы обучения для направлений подготовки бакалавров 140400, 131000. /Сост.: И.В.Терещенко, А.В.Братчиков, Л.В.Егорова; Кубан. гос.технол.ун-т. Каф. общей математики.-Краснодар: Изд.КубГТУ, 2011-41с.
Изложены программа дисциплины, варианты контрольных заданий, темы практических занятий, вопросы к зачету (или экзамену), рекомендуемая литература, приведены примеры выполнения и требования к оформлению контрольных работ.
Библиогр.: 6 назв.
Печатается по решению методического совета Кубанского государственного технологического университета
Рецензенты: канд. техн. наук, доц. С. В.Нестеров
канд. техн. наук, доцент Л.М.Данович
Содержание
Введение………………………………………………………………………..4
1 Инструкция по работе с учебно-методическими указаниями…………….5
2 Программа дисциплины …………………………………………………….5
3 Контрольные работы………………………………………………………...7
4 Задания на контрольные работы……….…………….……………………20
5 Содержание и оформление контрольных работ…………………………..37
6 Темы практических занятий……………………………………………….37
7 Вопросы для подготовки к экзамену (зачету)…………………………….38
8 Список рекомендуемой литературы……………………………………….39
Введение
Инженер в области математики должен иметь представление:
- о математике как особом способе познания мира, общности ее понятий и представлений;
- математическом моделировании;
- информации, методах ее хранения, разработки и передачи.
Знать и уметь использовать:
- основные понятия и методы математического анализа, аналитической геометрии, линейной алгебры, теории функций комплексного переменного, теории вероятностей и математической статистики, дискретной математики;
- математические модели простейших систем и процессов в естествознании и технике;
- вероятностные модели для конкретных процессов и проводить расчеты в рамках построенной модели.
Иметь опыт:
- употребления математической символики для выражения количественных и качественных отношений объектов;
- исследования моделей с учетом их иерархической структуры и оценки пределов применимости полученных результатов:
- использования основных приемов обработки экспериментальных данных;
- аналитического и численного решения алгебраических уравнений;
- исследования, аналитического и численного решения обыкновенных дифференциальных уравнений;
- аналитического и численного решения основных уравнений математической физики;
- программирования и использования возможностей вычислительной техники и программного обеспечения.
Цель курса «Математика»:
- дать студентам необходимую математическую подготовку для изучения общенаучных, общеинженерных и специальных дисциплин;
- привить студентам навыки логического и алгоритмического мышления;
- овладеть методами исследования и решения математических и прикладных задач по специальности;
- выработать умения самостоятельно расширять математические знания и применять их при анализе инженерных задач.
Инструкция по работе с учебно–методическим пособием
В разделе «Программа дисциплины» приведены темы и указывается, что необходимо знать в пределах каждой темы. В конце тем приводятся вопросы для самопроверки и литература из списка рекомендуемой литературы с указанием глав, страниц, где излагается материал темы.
Пример
Литература: [2, гл.2 c. 3-9], [4, c. 143-162],
где 2 и 4 – порядковые номера литературных источников из списка рекомендуемой литературы.
Вариант контрольного задания выбирается по последней цифре шифра зачётной книжки. Последняя цифра шифра (0) соответствует 10 варианту в контрольном задании. В контрольной работе выполняются номера задач, оканчивающиеся на номер варианта. Например, последняя цифра 4, значит, выполняются задачи 214, 224, 234 и т.д.
В разделе «Темы практических занятий» приводятся наименования практических занятий, которые будут проводиться в период экзаменационной сессии, и указывается литература для подготовки.
Программа дисциплины
Тема 1. Элементы линейной и векторной алгебры.
Определители второго и третьего порядков, их свойства, вычисление. Решение систем линейных уравнений по формулам Крамера. Понятие вектора. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты. Некоторые приложения. Векторное произведение векторов и его свойства. Выражение векторного произведения через координаты. Некоторые приложения. Смешанное произведение векторов и его свойства и геометрический смысл. Выражение смешанного произведения через координаты. Некоторые приложения.
Литература: [3, c. 123 – 129, 153 – 165], [4, c. 259 – 268, 223 – 239 ]
Вопросы для самоконтроля
1. Вычисление определителя третьего порядка.
2. Решение систем линейных уравнений по правилу Крамера.
3. Определение скалярного произведения векторов.
4. Понятие векторного произведения векторов, его приложения.
5. Смешанное произведение векторов, его приложения.
Тема 2.Элементы аналитической геометрии
Прямая на плоскости. Различные формы уравнения прямой на плоскости. Плоскость в пространстве. Прямая в пространстве. Взаимное расположение прямой и плоскости. Кривые второго порядка.
Литература: [2, с. 15-23], [4, гл.3 c. 43-49, гл.9 с.244-252].
Вопросы для самоконтроля
1. Уравнения прямой на плоскости.
2. Взаимное расположение прямых на плоскости.
3. Плоскость в пространстве. Уравнение плоскости, проходящей через три точки, уравнение плоскости по точке и нормали.
4. Угол между плоскостями.
5. Уравнения прямой в пространстве.
6. Кривые второго порядка.
Тема 3. Комплексные числа
Комплексные числа и действия над ними в алгебраической форме. Модуль и аргумент комплексного числа. Тригонометрическая и показательная формы комплексного числа. Формула Эйлера. Формула Муавра. Корни целой степени из комплексных чисел. Корни алгебраических уравнений на множестве комплексных чисел.
Литература:[1, гл. 7 §1-5].
Вопросы для самоконтроля
1. Дать определение комплексных чисел и действий над ними.
2. Нахождение модуля и аргумента комплексного числа.
3. Нахождение тригонометрической и показательной форм комплексного числа.
4. Нахождение корней целой степени из комплексных чисел.
Тема 4. Введение в математический анализ.
Понятие функции. Предел функции. Односторонние пределы. Предел функции при х→∞. Бесконечно малые и бесконечно большие функции, связь между ними. Основные теоремы о пределах. Первый и второй замечательный пределы. Непрерывность функции. Свойства функций, непрерывных на отрезке. Точки разрыва и их классификация.
Литература: [1, гл.2 §2-11], [4, гл.4 §2-9].
Вопросы для самоконтроля
1. Что называется пределом функции.
2. Бесконечно малые и бесконечно большие функции.
3. Раскрытие неопределенностей 0/0 и ∞/∞.
4. Первый и второй замечательный пределы, их следствия.
5. Дать определение непрерывности функции.
6. Точки разрыва и их классификация.
Тема 5. Дифференциальное исчисление
Производная функции, ее геометрический смысл. Основные правила и формулы дифференцирования. Производная сложной, обратной функции. Производные высших порядков. Некоторые теоремы о дифференцируемых функциях. Приложения производной. Правило Лопиталя. Условия монотонности функций. Необходимое и достаточное условия экстремума. Выпуклость и вогнутость, точки перегиба графика функции. Асимптоты. Общая схема исследования функции.
Литература:[1, гл.3 §2-16, гл.5 §2-11], [4, гл.5 §1-7, гл.6 §2,4], [2, гл.7 §1,2].
Вопросы для самоконтроля
1. Дать определение производной функции, ее геометрический и физический смысл.
2. Сформулировать основные правила дифференцирования.
3. Основные приложения производной.
4. Как определить промежутки монотонности и экстремумы функции.
5. Сформулировать необходимое и достаточное условия экстремума.
6. Определение выпуклости и вогнутости, точек перегиба графика функции.
7. Нахождение асимптот графика функции.
Контрольные работы
Программой дисциплины «Математика» для студентов I курса в первом семестре предусмотрено выполнение одной контрольной работы.
При выполнении контрольной работы необходимо изучить элементы линейной и векторной алгебры, аналитической геометрии на плоскости и в пространстве, а также ознакомиться с теорией кривых второго порядка и комплексными числами. Необходимо научиться вычислять основные типы пределов - неопределенности 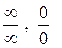 , первый и второй замечательный пределы. Изучить понятие непрерывности функции, основы дифференциального исчисления функции одной переменной, а также их приложения к исследованию функции.
, первый и второй замечательный пределы. Изучить понятие непрерывности функции, основы дифференциального исчисления функции одной переменной, а также их приложения к исследованию функции.
Ниже приведены примеры выполнения расчетов.
К заданиям 1-10
Пример. Доказать, что векторы 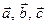 линейно независимы и найти разложение вектора
линейно независимы и найти разложение вектора 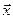 по векторам
по векторам 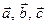 .
.
Решение. 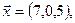
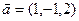 ,
, 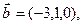
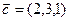 . Покажем, что векторы
. Покажем, что векторы 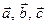 - некомпланарны. Для этого найдем их смешанное произведение:
- некомпланарны. Для этого найдем их смешанное произведение:
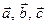 =
= 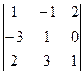 = 1 – 18 - 0 - 4 - 0- 3 = - 24.
= 1 – 18 - 0 - 4 - 0- 3 = - 24.
Так как смешанное произведение отлично от нуля, то векторы 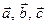 линейно независимы. Найдем разложение вектора
линейно независимы. Найдем разложение вектора 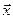 по векторам
по векторам 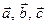 , т.е.
, т.е. 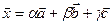 , где
, где 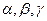 - неизвестные величины; для нахождения этих величин составим систему трех уравнений:
- неизвестные величины; для нахождения этих величин составим систему трех уравнений:
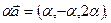
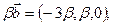
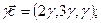
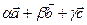 =
= 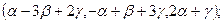
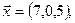
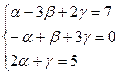 .
.
Решим эту систему методом Гаусса. Первое уравнение оставим без изменения, для получения второго сложим два первых, а третье сложим с первым, умножим на (-2):
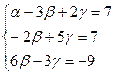 <=>
<=> 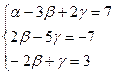 .
.
Первые два уравнения последней системы оставим без изменения, а третье сложим со вторым:
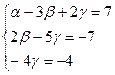 <=>
<=> 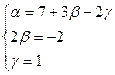 <=>
<=> 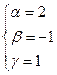 .
.
Таким образом, 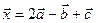 .
.
Ответ: 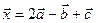 .
.
К заданиям 11-20По координатам вершины пирамиды А1А2А3А4 найти:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А4;
3) площадь грани А1А2А3;
4) объем пирамиды;
5) уравнения плоскостей А1А2А3 и А1А2А4 ;
6) угол между плоскостями А1А2А3 и А1А2А4.
1) Если заданы точки A1(x1, y1, z1) , А2(x2, y2, z2), то координаты вектора:
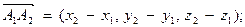
тогда длина вектора вычисляется по формуле 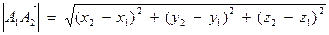 .
.
2) Из определения скалярного произведения следует, что угол между векторами вычисляется по формуле
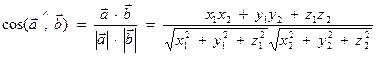 .
.
3) 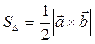 - площадь треугольника, построенного на векторах
- площадь треугольника, построенного на векторах 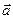 и
и 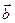 .
.
4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу вычисления объема пирамиды : 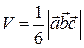 .
.
5) Если даны три точки А1(x1; y1; z1), А2(x2; y2; z2) и А3(x3; y3; z3), то уравнение плоскости, проходящей через три точки,находится по формуле
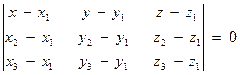 (1)
(1)
Например
Составитьуравнение плоскости, проходящей через три точки А1 , А2 ,А3, если А1(-3, 2, 0), А2(-2, 0, 2), А3(0, 3, -1).
Решение: по формуле (1) получим 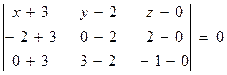 ,
, 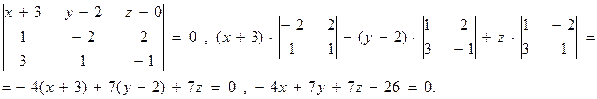
Итак, уравнение плоскости имеет вид −4х+7у+7z-26=0, где нормаль имеет координаты N(-4; 7; 7).
6) Угол, образованный двумя плоскостями, находится по формуле
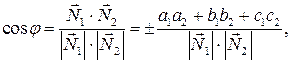 где
где 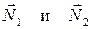 - нормали плоскостей.
- нормали плоскостей.
К заданиям 21-30
Пример. Найти уравнение данной кривой в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью: 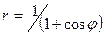 .
.
Связь между полярными и прямоугольными координатами точки устанавливаются формулами: 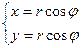
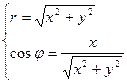
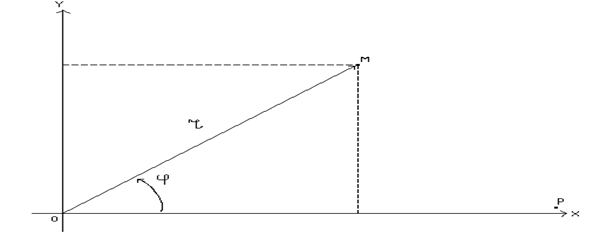
По условию 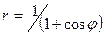 , имеем
, имеем 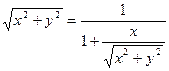 ;
;
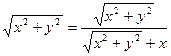 ;
; 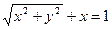 ;
;
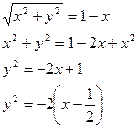
Это каноническое уравнение параболы с вершиной в точке 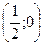 .
.
К заданиям 31-40Найти решение системы с помощью правила Крамера
Для систем трех уравнений с тремя неизвестными
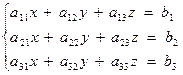
правило Крамера имеет вид: 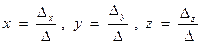 ,
,
где 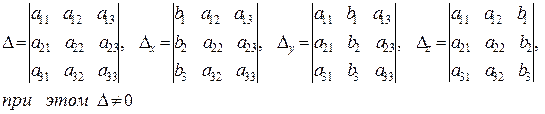
Определитель третьего порядка, обозначаемый символом
∆= 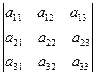 ,
,
вычисляется по правилу треугольника:
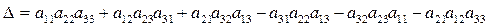 .
.
Например
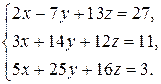
Решение.
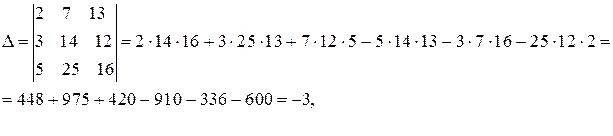
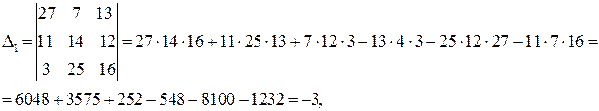
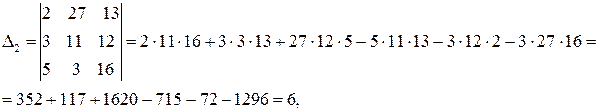
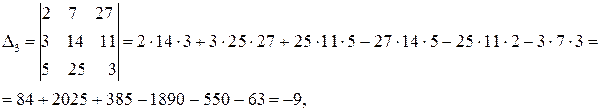
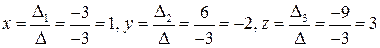 .
.
Ответ: (1, -2, 3).
Применение метода Гаусса приведено в примере к заданиям 1-10.
К заданиям 41 ‑ 50
Прмиер. Представить число 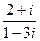 в алгебраической форме.
в алгебраической форме.
Решение.
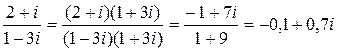 .
.
Пример. Представить число 1+i в тригонометрической форме.
Решение
Вычислим модуль
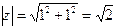 .
.
Найдем аргумент из системы уравнений
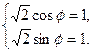
Поделим второе уравнение на первое, получим
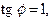
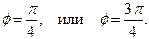
Системе уравнений удовлетворяет значение 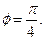 Следовательно, тригонометрическая форма имеет вид
Следовательно, тригонометрическая форма имеет вид
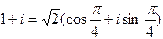 .
.
К заданиям 51-60
Вычислить пределы функций, не пользуясь правилом Лопиталя.
При вычислении предела дробно-рациональной функции при 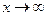 числитель и знаменатель дроби—величины бесконечно большие, т.е. получаем выражение
числитель и знаменатель дроби—величины бесконечно большие, т.е. получаем выражение 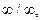 которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень х.
которое представляет собой неопределённость. Для вычисления предела этой функции нужно числитель и знаменатель дроби разделить на наивысшую степень х.
Пример 1.
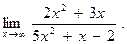
Решение. Для вычисления предела этой функции нужно числитель и знаменатель разделить на 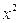 :
:
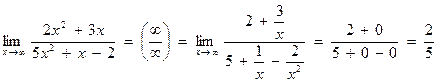
(при 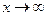 слагаемые
слагаемые 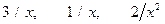 — величины бесконечно малые и, следовательно, их пределы равны нулю).
— величины бесконечно малые и, следовательно, их пределы равны нулю).
В том случае, когда при вычислении предела дробно-рациональной функции при 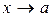 числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность
числитель и знаменатель имеют предел, равный нулю, т.е. имеем неопределенность 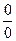 , надо разделить их на
, надо разделить их на 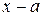 и перейти к пределу. Если после деления окажется, что при
и перейти к пределу. Если после деления окажется, что при 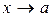 числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на
числитель и знаменатель снова имеют пределы, равные нулю, то надо произвести повторное деление на 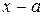 .
.
Пример 2.
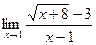 .
.
Здесь мы имеем неопределенность вида 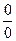 . Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавимся от иррациональности в числителе):
. Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавимся от иррациональности в числителе):
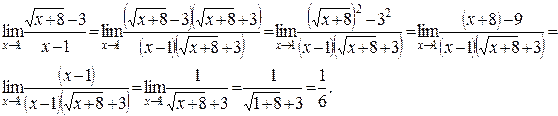 .
.
При вычислении пределов тригонометрических функций часто используется первый замечательный предел и его следствия:
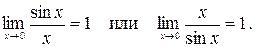
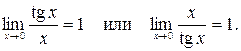
Пример 3.
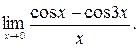
Решение. Преобразовав разность косинусов в произведение, получим
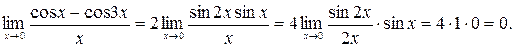
Если в пределе получаем неопределенность 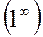 , используем второй замечательный предел
, используем второй замечательный предел 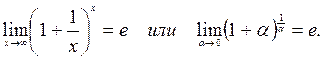 (2)
(2)
Пример 4.
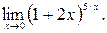
Решение. Выполнив преобразования и применив второй замечательный предел, найдём 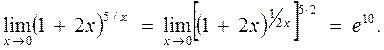
Пример 5.
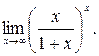
Решение. Выполнив преобразования и применив формулу (2), найдём
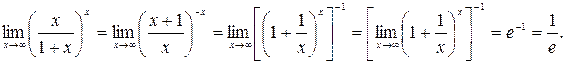
К заданиям 61-70
Пример. Задана функция 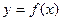 . Найти точки разрыва и определить их тип. Сделать схематический чертеж.
. Найти точки разрыва и определить их тип. Сделать схематический чертеж.
если 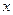 <1,
<1,
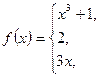 если
если 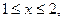
если 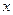 >2.
>2.
Решение. Функции 
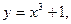
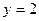 ,
, 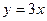 непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках
непрерывны на всей числовой прямой, поэтому данная функция может иметь разрывы только в точках, где меняется ее аналитическое выражение, т.е. в точках 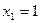 и
и 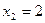 .
.
Исследуем функцию на непрерывность в этих точках, для чего найдем соответствующие односторонние пределы и значения функции. В точке 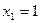
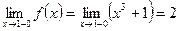 ,
,
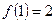 . Таким образом,
. Таким образом, 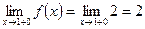
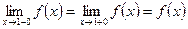 . Значит функция непрерывна в точке
. Значит функция непрерывна в точке 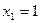 .
.
В точке 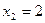
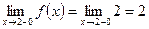 ,
, 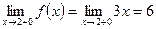 .
. 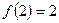
Таким образом, 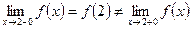 , т.е. функция имеет разрыв Ι рода и непрерывна слева. Скачок функции
, т.е. функция имеет разрыв Ι рода и непрерывна слева. Скачок функции 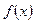 в точке
в точке 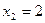 равен ∆
равен ∆ 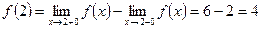 .
.
График функции изображен на рисунке
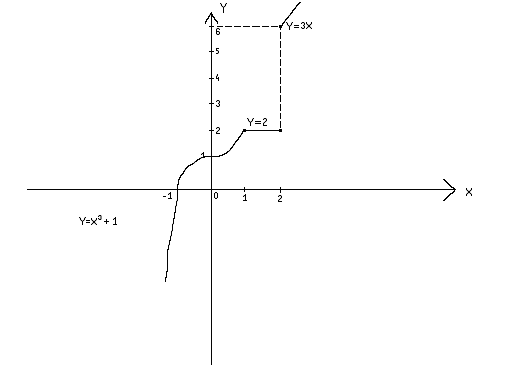
К заданиям 71-80
При выполнении данного задания необходимо знать правила вычисления производной (производная суммы, произведения и частного дух функций), а также изучить таблицу производных.
Пример. Найти производные 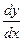 данных функций.
данных функций.
а). 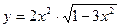
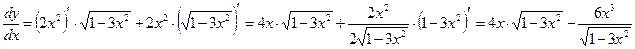 б).
б). 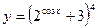
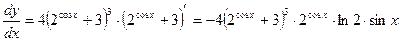 .
.
в). 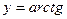
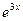
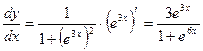 .
.
г). 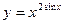
Прологарифмируем обе части равенства 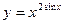 . Тогда
. Тогда 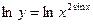 , т.е.
, т.е. 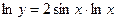 . Теперь продифференцируем последнее равенство
. Теперь продифференцируем последнее равенство
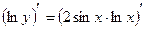 , т.е.
, т.е. 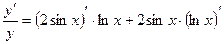 или
или 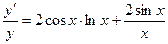 .
.
Отсюда 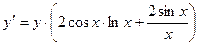 . Учитывая, что
. Учитывая, что 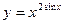 , имеем
, имеем 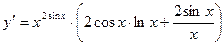 .
.
д). 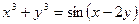 .
.
Дифференцируя обе части уравнения и учитывая, что 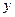 - есть функция от
- есть функция от 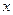 (поэтому, например,
(поэтому, например, 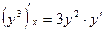 ), получим
), получим 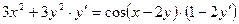 или
или
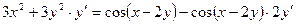
Отсюда находим 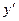 :
: 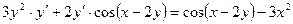 или
или
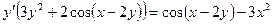 т.е.
т.е. 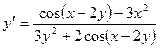 .
.
К заданиям 81-90
Пример. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции 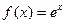 , вычислить значение
, вычислить значение 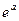 с точностью до 0,0001. a=0,5.
с точностью до 0,0001. a=0,5.
Решение. Применив разложение 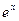 , получаем
, получаем 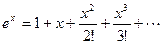
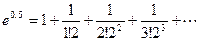 .
.
Определим число n так, чтобы погрешность приближенного равенства 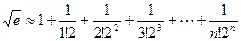 не превышала 0,0001. Погрешность этого равенства определяется суммой членов, следующих после
не превышала 0,0001. Погрешность этого равенства определяется суммой членов, следующих после 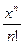 в разложении
в разложении 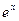 :
:
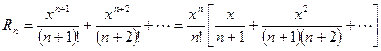 .
.
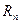 <
< 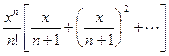 .
.
Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:
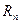 <
< 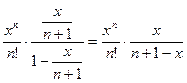 . Полагаем
. Полагаем 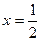 , тогда
, тогда 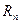 <
< 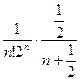 , т.е.
, т.е. 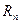 <
< 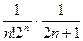 . Путем подбора определяем, при каком значении
. Путем подбора определяем, при каком значении 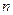 будет выполняться
будет выполняться 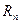 <0,0001. Получаем, что при
<0,0001. Получаем, что при 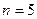
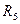 <
< 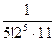 ,
, 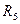 <0,0001. Итак, принимаем
<0,0001. Итак, принимаем 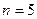 .
.
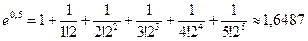 .
.
К заданиям 91-100 и 101-110
Общая схема исследования функции и построения графика.
1. Найти область определения функции.
2. Определить тип функции (четность, нечетность).
3. Найти точки пересечения с осями координат и интервалы
знакопостоянства функции.
4. Найти асимптоты графика функции:
а) вертикальные; б) невертикальные (наклонные).
5. Найти точки возможного экстремума и интервалы возрастания и
убывания функции.
6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.
7. Найти дополнительные точки.
8. Построить график функции, учитывая проведенные исследования.
Пример. Исследовать функцию 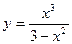 и построить ее график.
и построить ее график.
Решение
1. 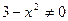 ,
, 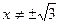 .
.
Область определения функции: 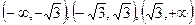 .
.
Точки разрыва: 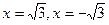 .
.
2. 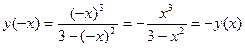 . Так как
. Так как 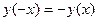 , то функция нечетная. Следовательно, ее график симметричен относительно точки О.
, то функция нечетная. Следовательно, ее график симметричен относительно точки О.
3. 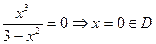 .
.
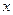 | 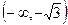 | 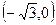 | 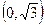 | 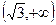 | |
знак 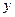 | + | - | + | - | |
| Расположение графика | Выше оси Ох | Ниже оси Ох | Пересекает ось Ох | Выше оси Ох | Ниже оси Ох |
4. а). Вертикальные асимптоты:
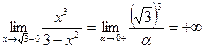 ;
; 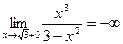 .
.
Следовательно, 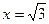 - точка разрыва второго рода. По свойству симметрии функции
- точка разрыва второго рода. По свойству симметрии функции 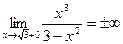 . Поэтому уравнения вертикальных асимптот
. Поэтому уравнения вертикальных асимптот 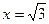 и
и 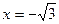 .
.
Других вертикальных асимптот график не имеет.
б). Наклонные асимптоты 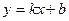 :
:
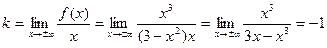 ;
;
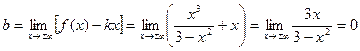 .
. 
Итак, 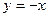 - уравнение наклонной асимптоты графика функции.
- уравнение наклонной асимптоты графика функции.
5. 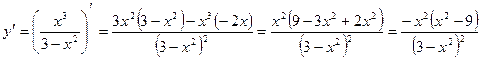 .
.
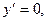
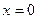 ,
, 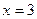 ,
, 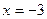 - критические точки.
- критические точки.
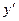 не существует при
не существует при 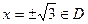 , поэтому
, поэтому 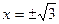 не является критическими точками.
не является критическими точками.
| X | 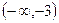 | -3 | 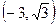 | 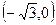 | 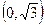 | 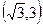 |  | ||
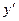 | - | + | + | + | + | - | |||
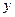 |   | 4,5 min |  |  | Нет экст. |  |  | -4,5 max |  |
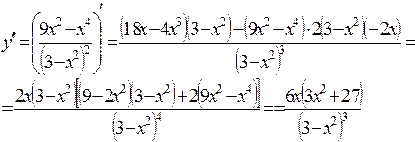
6. 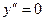 ;
; 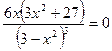 при
при 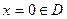 критическая точка.
критическая точка.
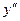 не существует при
не существует при 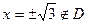 . Следовательно, имеется одна критическая точка
. Следовательно, имеется одна критическая точка 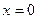 .
.
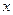 | 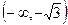  | 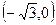 | 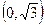 | 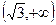 | |
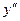 | + | - | + | - | |
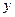 |  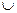 | 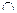 |  |  |
7. Дополнительные точки
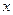 | 0,5 | 1,5 | 3,5 | |||
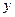 | 0,05 | 0,5 | 4,5 | -8 | -4,6 | -5 |
8.Строим график функции.
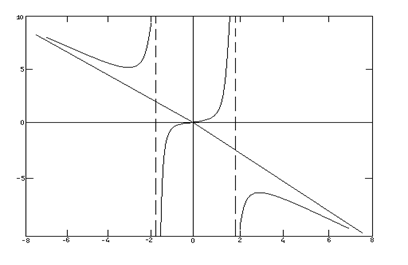
Задания на контрольную работу
Задачи 1-10 Даны векторы 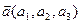 ,
, 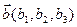 ,
, 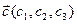 и
и 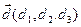 в некотором декартовом базисе. Показать, что векторы
в некотором декартовом базисе. Показать, что векторы 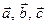 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 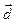 в этом базисе.
в этом базисе.
1. 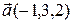 , , 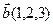 , , 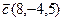 , , 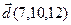 ; ; |
2. 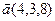 , , 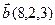 , , 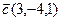 , , 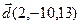 ; ; |
3. 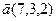 , , 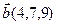 , , 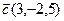 , , 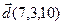 ; ; |
4. 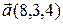 , , 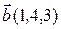 , , 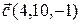 , , 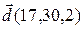 ; ; |
5. 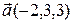 , , 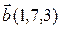 , , 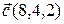 , , 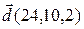 ; ; |
6. 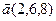 , , 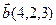 , , 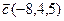 , , 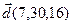 ; ; |
7. 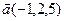 , , 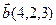 , , 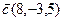 , , 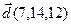 ; ; |
8. 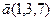 , , 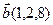 , , 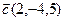 , , 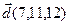 ; ; |
9. 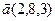 , , 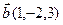 , , 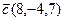 , , 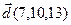 ; ; |
10. 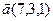 , , 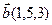 , , 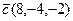 , , 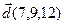 . . |
Задачи 11-20 Даны декартовы координаты вершин пирамиды 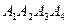 . Найти:
. Найти:
1. длину ребер 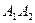 ,
, 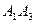 и
и 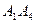 ;
;
2. угол между ребрами 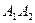 и
и 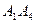 ;
;
3. угол между ребром 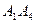 и гранью
и гранью 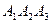 ;
;
4. площадь грани 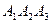 ;
;
5. объем пирамиды;
6. уравнение прямой 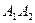 ;
;
7. уравнение плоскости 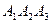 ;
;
8. уравнение высоты, опущенной из вершины 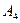 на грань
на грань 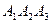 ;
;
9. сделать чертеж.
11. A1(1,3,6), A2(9,6,7), A3(0,7,2), A4(10,5,0).
12. A1(2,3,6), A2(8,6,7), A3(1,7,2), A4(9,5,0).
13. A1(3,3,6), A2(7,6,7), A3(2,7,2), A4(8,5,0).
14. A1(4,3,6), A2(6,6,7), A3(3,7,2), A4(7,5,0).
15. A1(5,3,6), A2(5,6,7), A3(4,7,2), A4(6,5,0).
16. A1(6,3,6), A2(4,6,7), A3(5,7,2), A4(5,5,0).
17. A1(7,3,6), A2(3,6,7), A3(6,7,2), A4(4,5,0).
18. A1(8,3,6), A2(2,6,7), A3(7,7,2), A4(3,5,0).
19. A1(9,3,6), A2(1,6,7), A3(8,7,2), A4(2,5,0).
20. A1(10,3,6), A2(0,6,7), A3(9,7,2), A4(1,5,0).
Задачи 21-30Кривая задана уравнением 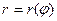 в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1) построить линию по точкам на отрезке 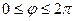 , придавая
, придавая 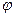 значения через промежуток
значения через промежуток 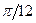 ;
;
2) найти уравнение данной кривой в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
3) по уравнению в декартовой системе координат определить, какая это кривая.
21. 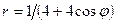 .
.
22. 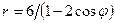 .
.
23. 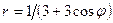 .
.
26. 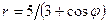 .
.
27. 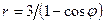 .
.
28. 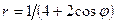 .
.
24. 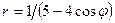 .
.
25. 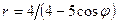 .
.
29. 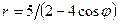 .
.
30. 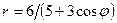 .
.
Задачи 31 ‑ 40 Дана система линейных уравнений
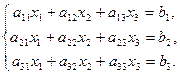
Найти ее решения по правилу Крамера и методом Гаусса.
31. 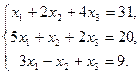
32. 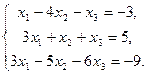
33. 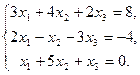
34. 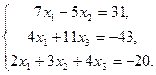
35. 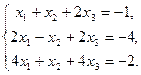
36. 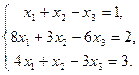
37. 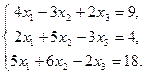
38. 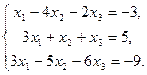
39. 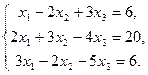
40. 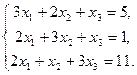
Задачи 41 ‑ 50Дано комплексное число z. Требуется:
1) записать число z в алгебраической, тригонометрической и показательной формах.
2) Найти все кубические корни числа z.
41. 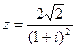 .
.
42. 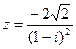 .
.
43. 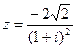 .
.
44. 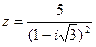 .
.
45. 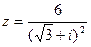 .
.
46. 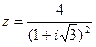 .
.
47. 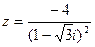 .
.
48. 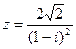 .
.
49. 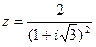 .
.
50. 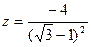 .
.
Задачи 51-60Найти пределы функций, не пользуясь правилом Лопиталя.
51.a) 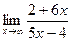 ; б)
; б) 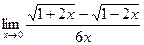 ; в)
; в) 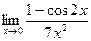 ; г)
; г) 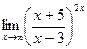 .
.
52.a) 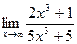 ; б)
; б) 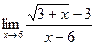 ; в)
; в) 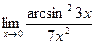 ; г)
; г) 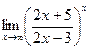 .
.
53.a) 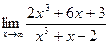 ; б)
; б) 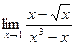 ; в)
; в) 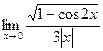 ; г)
; г) 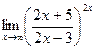 .
.
54.a) 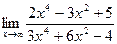 ; б)
; б) 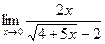 ; в)
; в) 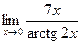 ; г)
; г) 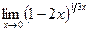 .
.
55.a) 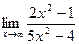 ; б)
; б) 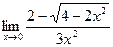 ; в)
; в) 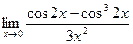 ; г)
; г) 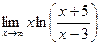 .
.
56.a) 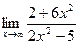 ; б)
; б) 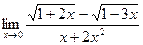 ; в)
; в) 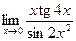 ; г)
; г) 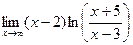 .
.
57.a) 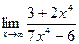 ; б)
; б) 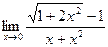 ; в)
; в) 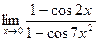 ; г)
; г) 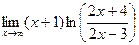 .
.
58.a) 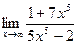 ; б)
; б) 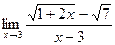 ; в)
; в) 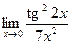 ; г)
; г) 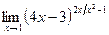 .
.
59.a) 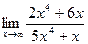 ; б)
; б) 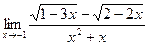 ; в)
; в) 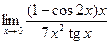 ; г)
; г) 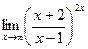 .
.
60.a) 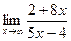 ; б)
; б) 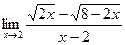 ; в)
; в) 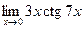 ; г)
; г) 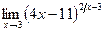 .
.
Задачи 61-70Задана функция 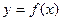 . Найти точки разрыва и определить их тип. Сделать схематический чертеж.
. Найти точки разрыва и определить их тип. Сделать схематический чертеж.
61. 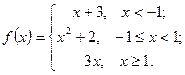
62. 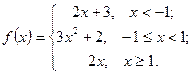
63. 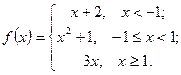
64. 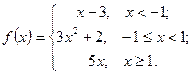
65. 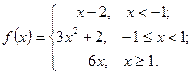
66. 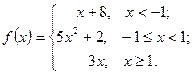
67. 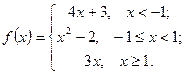
68. 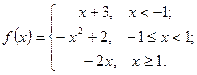
69. 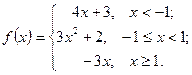
70. 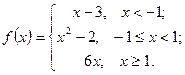
Задачи 71-80Найти производные 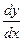 данных функций.
данных функций.
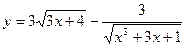
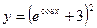 ;
;
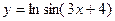 ;
;
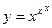 ;
;
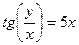 .
.
72.
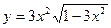 ;
;
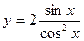 ;
;
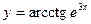 ;
;
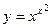 ;
;
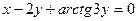 .
.
73.
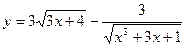 ;
;
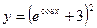 ;
;
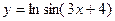 ;
;
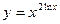 ;
;
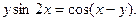
74.
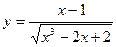 ;
;
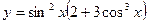 ;
;
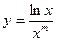 ;
;
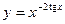 ;
;
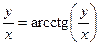 .
.
75.
