Для простого модуля старший коефіцієнт взаємнопростий з ним. Визначимо множник k так, щоб . Матимемо . Домножаючи обидві частини заданої конгруенції на 10 за модулем 13, дістаємо 1 страница
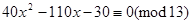 ,
,
або 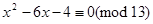 .
.
Виділимо в лівій частині цієї конгруенції повний квадрат
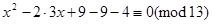 ,
,
або 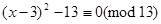 .
.
Остаточно 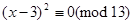 .
.
Отже, 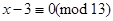 або
або 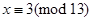 .
.
III. За критерієм Ейлера знайти всі квадратні лишки за модулем 11.
Розв`язання.
За критерієм Ейлера при простому непарному p число a є квадратичним лишком за модулем p тоді і тільки тоді, коли 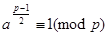 , і квадратичним нелишком тоді і тільки тоді, коли
, і квадратичним нелишком тоді і тільки тоді, коли 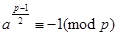 .
.
Отже, для розв`язання задачі випробуємо числа 1, 2, 3, .., 10 за допомогою критерія Ейлера. Маємо
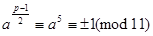 , тоді
, тоді
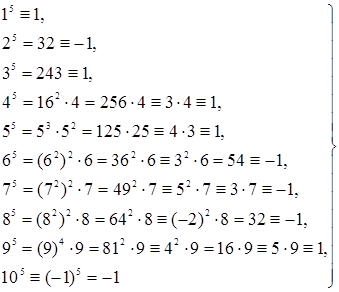 (mod 11).
(mod 11).
Тому числа 1, 3, 4, 5, 9 – квадратичні лишки за модулем 11.
IV. Знайти порядок числа a = 2 за модулем m = 15.
Розв`язання.
Щоб знайти порядок  числа a за модулем m, необхідне виконання таких вимог:
числа a за модулем m, необхідне виконання таких вимог:
1.) (a, m)=1;
2.) 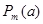 - дільник числа
- дільник числа 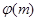 ;
;
3.) 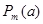 - найменше з тих натуральних чисел k, для яких виконується конгруенція
- найменше з тих натуральних чисел k, для яких виконується конгруенція 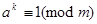 .
.
Маємо (2, 15)=1; знаходимо 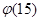 :
:
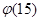 =
= 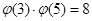 .
.
Отже, 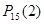 міститься серед чисел 1, 2, 4, 8. Записуємо послідовно:
міститься серед чисел 1, 2, 4, 8. Записуємо послідовно:

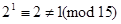 ,
,
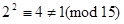 ,
,
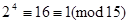 .
.
Отже, 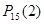 =4.
=4.
V. Знайти всі первісні корені за модулем m=7.
Розв`язання.
Первісних коренів за простим модулем m=7 є 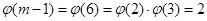 . Вони містяться серед чисел
. Вони містяться серед чисел 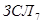 :
:
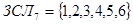 .
.
Оскільки m-1=6 у канонічному розкладі має вигляд 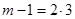 , то досліджувати слід числа виду
, то досліджувати слід числа виду 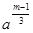 і
і 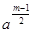 , тобто числа
, тобто числа 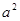 і
і 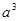 . Де
. Де 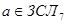 .
.
Знайдемо перший первісний корінь. Перевіряємо число 2.
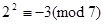 ,
,
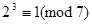 .
.
Оскільки 3<6, то 2 не є первісним коренем за модулем 7.
Тоді 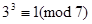 . Отже, порядком числа 3 є 6, тобто 3 є первісним коренем за модулем 7.
. Отже, порядком числа 3 є 6, тобто 3 є первісним коренем за модулем 7.
Другий первісний корінь міститься серед чисел виду 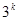 , де (k, m-1)=(k, 6)=1 і 1<k<6/
, де (k, m-1)=(k, 6)=1 і 1<k<6/
Цій умові задовільняє тільки число k=5. отже, другим первісним коренем є число 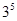 . Оскільки
. Оскільки 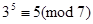 , то первісними коренями за модулем 7 є числа 3 і 5.
, то первісними коренями за модулем 7 є числа 3 і 5.
VI. Розв`язати конгруенцію 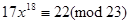 . (1)
. (1)
Розв`язання.
Беремо індекси від обох частин конгруенції
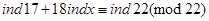 .
.
За таблицею індексів маємо:
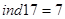 ;
; 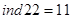 і тому
і тому
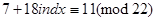 , або
, або
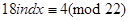 (2)
(2)
Дістали лінійну конгруенцію відносно ind x . Розв`яжемо її. Оскільки (18, 22)=2 і 4 ділиться на 2, то ця конгруенція має 2 розв`язки.
Скоротимо спочатку обидві частини і модуль на 2:
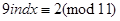 .
.
До правої частини додамо число –11:
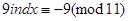 .
.
Скоротимо обидві частини на 9:
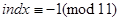 .
.
Дістаємо розв`язки конгруенції (2):
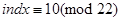 ,
,
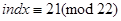 .
.
За таблицею антиіндексів знаходимо відповідні два значення невідомого x:
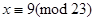 ,
, 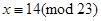 .
.
VII. Знайти найменше натуральне число x, яке задовольняє наступну конгруенцію 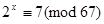 .
.
Розв`язання.
Індексуємо конгруенцію:
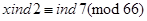 .
.
За таблицями індексів:
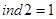 ;
;
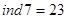 , одержуємо
, одержуємо
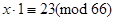 .
.
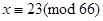 , або
, або  при k=0, 1, 2, ..
при k=0, 1, 2, ..
VIII. Знайти остачу від ділення 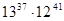 на 35.
на 35.
Розв`язання.
Скористаємося теоремами Ейлера і Ферма.
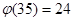 ; (13, 35)=(12, 35) = 1, тому
; (13, 35)=(12, 35) = 1, тому 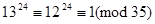 .
.
Тоді 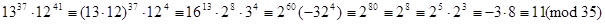 .
.
Отже, при діленні на 35 число 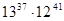 дає остачу 11.
дає остачу 11.
Контрольна робота № 9
І. Знайти найбільший спільний дільник многочленів f(x) і g(x) та підібрати такі многочлени m(x) і n(x), що f(x)m(x) + g(x)n(x) = d(x).
1) f(x) = x4 + x3 – 3x2 – 4x – 1; g(x) = x3 + x2 – x – 1;
2) f(x) = x6 – 7x4 + 8x3 – 7x + 7; g(x) = 3x5 – 7x3 + 3x2 – 7;
3) f(x) = x5 + x4 – x3 – 3x2 – 3x – 1; g(x) = x4 – 2x3 – x2 – 2x + 1;
4) f(x) = x4 – 10x2 +1; g(x) = x4 – 4 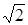 x3 + 6x2 + 4
x3 + 6x2 + 4 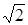 x + 1;
x + 1;
5) f(x) = x5 + 3x4 + x3 + x2 + 3x + 1; g(x) = x4 + 2x3 + x + 2;
6) f(x) = 4x4 – 2x3 – 16x2 + 5x + 9; g(x) = 2x3 – x2 – 4x + 4;
7) f(x) = x4 – x3 – 4x2 + 4x + 1; g(x) = x2 – x – 1;
8) f(x) = x5 – 5x4 – 2x3 + 12x2 – 2x + 12; g(x) = x3 – 5x2 – 3x + 17;
9) f(x) = 3x4 – 3x3 + 4x2 – x + 1; g(x) = 2x3 – x2 + x + 1;
10) f(x) = x4 + x3 + x2 + x + 1; g(x) = 4x3 + 3x2 + 2x + 1.
ІІ. Користуючись схемою Горнера:
а) розкласти многочлен f(x) за степенями (х – а) і одержаний розклад розташувати за спадними степенями х;
б) знайти канонічний розклад (відокремити кратні множники);
в) знайти значення многочлена f(x) та його похідних при х = а.
1) f(x) = x4 + 3x3 – 8x2 + 4x – 1; a = 2;
2) f(x) = x5 + 3x4 – 9x3 – 7x2 + 39x – 21; a = 1;
3) f(x) = x4 – 2x3 – 5x2 + 2x + 2; a = –2;
4) f(x) = x6 – 6x4 – 4x3 + 9x2 + 12x + 2; a = 3;
5) f(x) = x5 – 10x3 – 20x2 – 15x – 4; a = –1;
6) f(x) = x5 – 6x4 + 16x3 – 24x2 + 20x – 8; a = –3;
7) f(x) = x6 – 2x5 – x4 – 2x3 + 5x2 + 4x + 4; a = 1;
8) f(x) = x6 – 15x4 + 8x3 + 51x2 – 72x + 27; a = –1;
9) f(x) = x7 – 3x6 + 5x5 – 7x4 + 7x3 – 5x2 + 3x – 1; a = 2;
10) f(x) = 3x4 + 6x3 – 2x2 + 1; a = –1.
ІІІ. Знайти раціональні корені многочлена.
1) f(x) = x4 – 2x3 – 8x2 + 13x – 24;
2) f(x) = 6x4 + 19x3 – 7x2 – 26x + 12;
3) f(x) = x5 – 2x4 – 4x3 + 4x2 – 5x + 6;
4) f(x) = 10x4 – 13x3 + 15x2 – 18x – 24;
5) f(x) = x4 + 2x3 – 13x2 – 38x – 24;
6) f(x) = x4 + 4x3 – 2x2 – 12x + 9;
7) f(x) = x5 + x4 – 6x3 – 14x2 – 11x – 3;
8) f(x) = 2x3 + 3x2 + 6x – 4;
9) f(x) = 2x3 – 3x2 + 4x – 5;
10) f(x) = x4 – x3 – 22x2 + 16x + 96.
ІV. Виразити через елементарні симетричні многочлени такі многочлени:
1) f(x1, x2, x3) = x13 + x23 + x33 – x1 – x2 – x3;
2) f(x1, x2, x3) = x15x2x3 + x25x1x3 + x35x1x2 + 2x1x2x3;
3) f(x1, x2, x3) = x14x22 + x24x12 + x34x22 + x34x12 + x14x32 + x24x32;
4) f(x1, x2, x3) = x12x2 + x1x22 + x12x3 + x1x32 + x22x3 + x2x32;
5) f(x1, x2, x3) = x14 + x24 + x34 x13 –2x12x22 – 2x22x32 – 2x12x32;
6) f(x1, x2, x3) = (x1 – x2)2 + (x1 – x3)2 + (x2 – x3)2 ;
7) f(x1, x2, x3) = (x1 + x2 – 5x3) (x2 + x3 – 5x1) (x1 + x3 – 5x2);
8) f(x1, x2, x3) = 3x13 – 3x23 + 3x33 + x1 + x2 + x3;
9) f(x1, x2, x3) = 3x13 + 3x23 + 3x33 + 5x1x2x3 + 2x12 + 2x22 + 2x32;
10) f(x1, x2, x3) = (x1 – x2)(x2 – x3)(x3 – x1).
V. У множині дійсних чисел розв’язати такі системи рівнянь:
1) 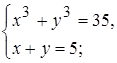 2)
2) 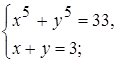 3)
3) 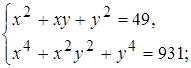
4) 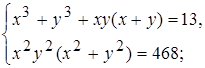 5)
5) 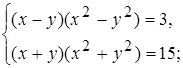
6) 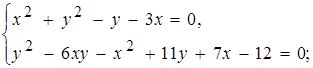 7)
7) 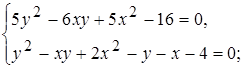
8) 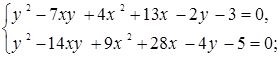 9)
9) 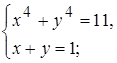
10) 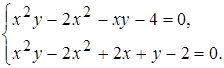
VI. Позбавитися від алгебраїчної ірраціональності в знаменнику дробу:
1) 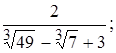 2)
2) 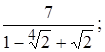 3)
3) 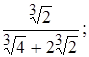
4) 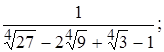 5)
5) 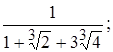
6) 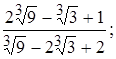 7)
7) 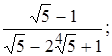 8)
8) 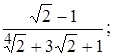
9) 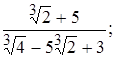 10)
10) 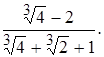
VІІ. Довести, що число a є алгебраїчним над полем Q і знайти його мінімальний многочлен, якщо:
1) 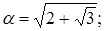 | 6) 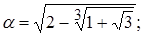 |
2) 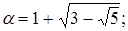 | 7) 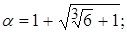 |
3) 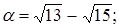 | 8) 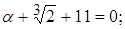 |
4) 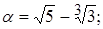 | 9) 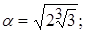 |
5) 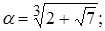 | 10) 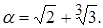 |
VІІІ. Розкласти на незвідні у полі Q множники такі многочлени:
1) f(x) = x4 + x3 – 6x2 – 7x – 7;
2) f(x) = x4 – x3 – 6x2 + 8x – 2;
3) f(x) = 6x4 – 13x3 + 12x2 – 13x + 6;
4) f(x) = 9x4 – 15x3 + 28x2 – 20x + 16;
5) f(x) = (x + 3)4 + (x + 5)4 – 16;
6) f(x) = (x + 1)6 – 9(x + 1)3 + 20;
7) f(x) = x4 + 4x3 + 4x2 + 1;
8) f(x) = x3 – 6x2 + 11x – 6;
9) f(x) = x4 + 3x3 – 3x2 – 11x – 6;
10) f(x) = x5 – x3 – x2 + 1.
| Варіант | Задачі |
| 1. | І.1, ІІ.1, ІІІ. 1, VІ.1, V.1, VІ.1, VІІ.1, VІІІ.1 |
| 2. | І.2, ІІ.2, ІІІ.2, VІ.2, V.2, VІ.2, VІІ.2, VІІІ.2 |
| 3. | І.3, ІІ.3, ІІІ.3, VІ.3, V.3, VІ.3, VІІ.3, VІІІ.3 |
| 4. | І.4, ІІ.4, ІІІ.4, VІ.4, V.4, VІ.4, VІІ.4, VІІІ.4 |
| 5. | І.5, ІІ.5, ІІІ.5, VІ.5, V.5, VІ.5, VІІ.5, VІІІ.5 |
| 6. | І.6, ІІ.6, ІІІ.6, VІ.6, V.6, VІ.6, VІІ.6, VІІІ.6 |
| 7. | І.7, ІІ.7, ІІІ.7, VІ.7, V.7, VІ.7, VІІ.7, VІІІ.7 |
| 8. | І.8, ІІ.8, ІІІ.8, VІ.8, V.8, VІ.8, VІІ.8, VІІІ.8 |
| 9. | І.9, ІІ.9, ІІІ.9, VІ.9, V.9, VІ.9, VІІ.9, VІІІ.9 |
| 10. | І.10, ІІ.10, ІІІ.10, VІ.10, V.10, VІ.10, VІІ.10, VІІІ.10 |
Зразки розв‘язання задач контрольної роботи № 9
1. Знайти найбільший спільний дільник многочленів f(x) і g(x) та підібрати такі многочлени m(x) і n(x), що f(x)m(x) + g(x)n(x) = d(x).
f(x) = 2x4 + 3x3 – 3x2 – 5x + 2;
g(x) = 2x3 + x2 – x – 1.
Розв‘язання.
До многочленів f(x) і g(x) застосовуємо алгоритм Евкліда:
| _ 2x4 + 3x3 – 3x2 – 5x + 2 | 2x3 + x2 – x – 1 | ||||||||
| 2x4 + x3 – x2 – x | х + 1 | ||||||||
| _ 2x3 – 2x2 – 4x + 2 | |||||||||
| 2x3 + x2 – x – 1 | |||||||||
| _ 2x3 + x2 – x – 1 | – 3x2 – 3x + 3 | ||||||||
| 2x3 + 2x2 – 2x | 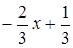 | ||||||||
| _ – x2 + x – 1 | |||||||||
| – x2 – x + 1 | |||||||||
| _ – 3x2 – 3x + 3 | 2х – 2 | ||||||||
| – 3x2 + 3x | 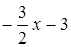 | ||||||||
| _ –6х + 3 | |||||||||
| –6х + 6 | |||||||||
| – 3. | |||||||||
Отже, в результаті ділення одержуємо:
f(x) = g(x)q1(x) + r1(x);
q1(x) = x + 1, r1(x) = –3x2 – 3x + 3;
g(x) = r1(x)q2(x) + r2(x);
q2(x) = 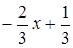 ; r2(x) = 2x – 2;
; r2(x) = 2x – 2;
r1(x) = r2(x)q3(x) + r3(x);
q3(x) = 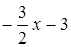 ; r3(x) = –3.
; r3(x) = –3.
Так як r3(x) = –3 є стале число, а на стале число без остачі ділиться будь-який многочлен, то наступна остача r4(x) буде дорівнювати нулю. Отже, алгоритм Евкліда записався тут у три рядки, а найбільший спільний дільник дорівнює – 3, або
d(x) = 1 = – 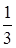 r3(x).
r3(x).
Щоб виразити d(x) через многочлени m(x) і n(x) виразимо спочатку через них r3(x).
r3(x) = r1(x) – r2(x) q3(x),
r3(x) = r1(x) – [g(x) – r1(x)q2(x)]q3(x),
або r3(x) = r1(x)[1 + q2(x)q3(x)] – g(x)q3(x).
В останню рівність замість r1(x) підставимо його вираз з першого рядка алгоритму Евкліда, одержимо:
r3(x) = [f(x) – g(x)q1(x)]×[1 + q2(x)q3(x)] – g(x)q3(x) =
= –f(x)[1 + q2(x)q3(x)] + g(x)[–q1(x) – q1(x)q2(x)q3(x) – q3(x)].
Враховуючи, що d(x) = – 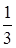 r3(x), маємо:
r3(x), маємо:
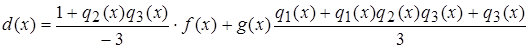 .
.
Отже, 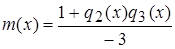 ;
;
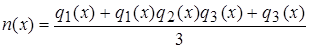 ,
,
де q1(x) = x + 1; q2(x) = 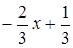 ; q3(x) =
; q3(x) = 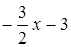 .
.
