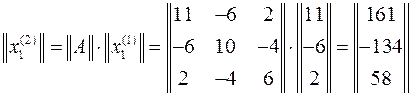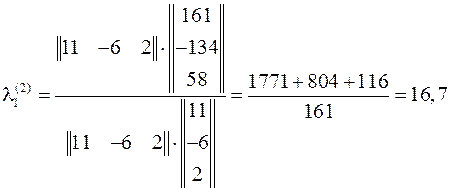Модальный анализ динамических свойств энергосистемы

Основные определения и вывод основных уравнений

Модальный анализустойчивости требует приведения модели энергосистемы к нормальному виду, т.е. все линеаризованные дифференциальные уравнения должны быть разрешены относительно производных по времени

,

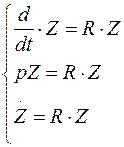где

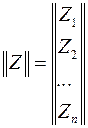- вектор переменных состояний системы порядка n,

R – квадратная матрица состояния системы, размером ,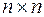

.

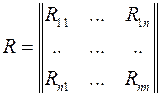Таким образом, для системы порядка n модель имеет вид

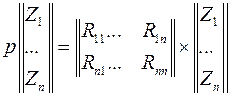
Система линейных уравнений малых колебаний для сложной энергосистемы

,

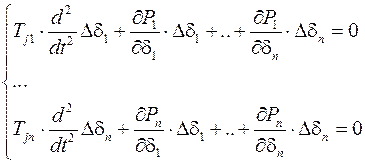записанная в матричной форме

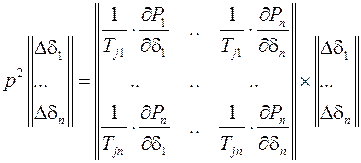
представляет собой модель, содержащую вторые производные переменных состояния по времени (в данном случае углов отклонения роторов от синхронной оси).

На примере одногенератороной системы можно рассмотреть приведение математической модели

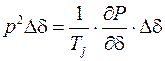
к нормальному виду.

Поскольку первая производная угла отклонения по времени является угловой скоростью

,

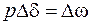следовательно

,

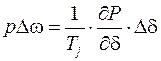откуда

.

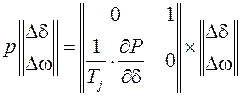Полученная модель приведена к форме, содержащей только первые производные по времени, за счет введения дополнительных переменных состояния и удвоения ранга матрицы состояния энергосистемы.

Решение системы для любой переменной состояния может быть записано в виде суммы составляющих движения

,

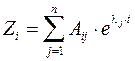где 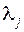– корень системы,

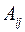– амплитуда движения, включающая два сомножителя

,

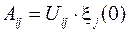где 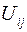– сомножитель, не зависящий от начальных условий и определяемый только параметрами системы,

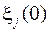– сомножитель, зависящий от начальных условий.

Таким образом, переменная состояния определяется из выражения

.

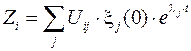Выражение для определения всей совокупности переменных состояния можно записать в виде системы уравнений

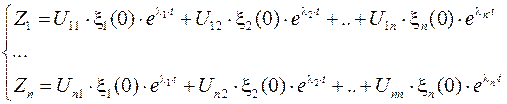
или в матричной форме

.

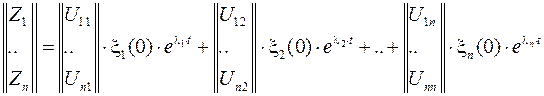Слагаемые правой части уравнения называется модами движения, а входящие в них столбцы – модальными векторами.

Пусть число генерирующих узлов n=2, переменные состояния 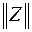– углы отклонения роторов генераторов от синхронной оси

В данном примере для двухгенераторной электроэнергетической системы

.

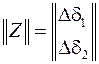Переменная состояния 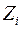– суперпозиция колебаний различной частоты ротора генератора при нарушении установившегося режима работы энергосистемы (см. рис. 45).

Угол отклонения ротора первого генератора от синхронной оси определяется по формуле

,

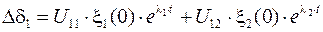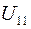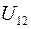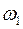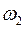где , – амплитуды колебаний с частотами и для ротора первого генератора;

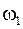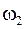, – собственные частоты малых колебаний первого и второго генераторов ( 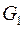и );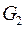

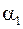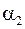, – их декременты затухания.

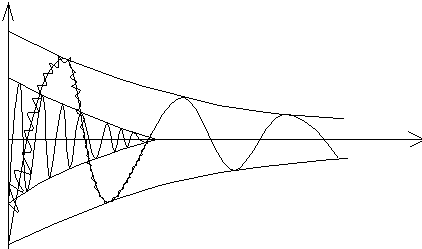
Рис. 45. Зависимость переменной состояния от времени

Для рассматриваемого примера состояние системы устойчиво т.к. суперпозиция колебаний обоих частот имеет тенденцию к затуханию (см. рис. 45).

В общем случае выражение для столбца переменных состояния может быть записано через квадратную модальную матрицу, столбцами которой являются модальные вектора

.

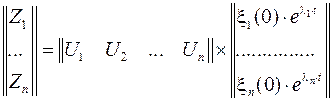Поскольку производная от экспоненты

,

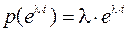следовательно, для левой части уравнения модели приведенной к нормальному виду

,

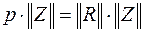верно выражение

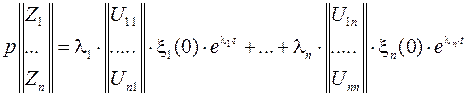
или же

.

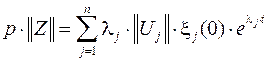Для правой части в свою очередь верно выражение

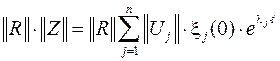
Таким образом, для каждого 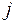-го корня 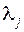выполняется следующее равенство

,

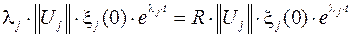что при сокращении сомножителей 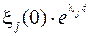дает уравнение

.

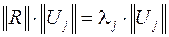Таким образом, полученное матричное уравнение не зависит от начальных условий и определяется только параметрами системы.

Из матричной алгебры известно, что если для некого числа 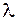верно

,

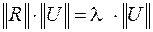где 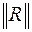– квадратная матрица, 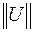– столбец, то 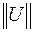– собственный вектор матрицы 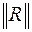, 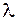– собственное значение .

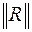Собственные значения определяются из условия

.

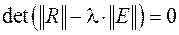Раскрытие характеристического определителя

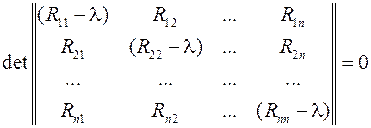
дает характеристическое уравнение

,

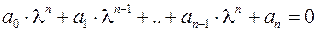решение которого позволяет найти все собственные значения.

Матрица 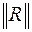размером 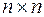имеет n собственных значений.

Собственные вектора определяются из уравнений

,

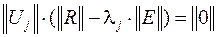где 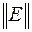- единичная матрица

,

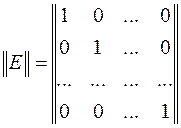в которое поочередно подставляются все собственные значения.

Каждое собственное значение соответствует определенному собственному вектору матрицы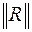

.

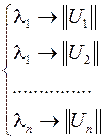Собственное значение может быть действительным корнем 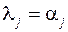(апериодическое движение) или одним из пары комплексно сопряженных корней 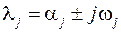(колебательное движение с частотой 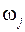и декрементом затухания ).

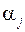Собственный вектор определяет соотношение амплитуд колебаний роторов генераторов с частотой 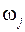, т.е. форму или же моду j-го движения)

.

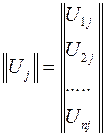Модальная матрица определяет совокупность всех мод движения. На рис. 46 показан временной срез моды – форма колебательного движения с частотой 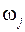для энергосистемы состоящей из пяти генераторных узлов (см. рис. 47). Высота столбца гистограммы над номером некого генератора, соответствует значению одного из элементов собственного вектора 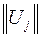, а в физическом смысле это амплитуда колебаний ротора данного генератора с указанной частотой .

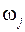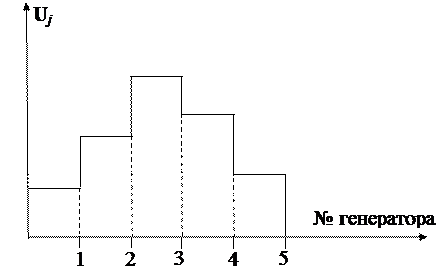
Рис. 46. Форма (мода) j-го движения

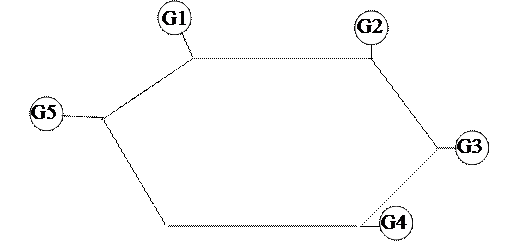
Рис. 47. Схема энергосистемы

Модальная теория изучает совокупность динамических свойств энергосистемы, на основании определения собственных значений и собственных векторов матрицы состояний энергосистемы.

Для определения собственного вектора необходимо решить следующую систему

.

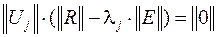Однако, т.к. 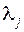– это корень из уравнения 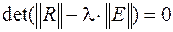, следовательно система данная будет линейно зависима. Для решения этой проблемы необходимо произвольно задать один из компонентов собственного вектора (например, 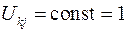), исключив тем самым одно из уравнений и решив систему 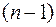порядка с 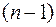неизвестным. В таком случае собственный вектор определяется с точностью до константы

.

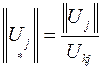Пусть математическая модель представлена системой уравнений второго порядка

,

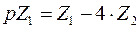
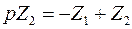которая при записи в матричной форме имеет вид

,

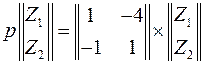где элементами столбцов являются переменные состояния, квадратная матрица – матрица состояния .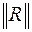

Собственные значения 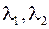матрицы состояния 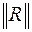определяются из условия

,

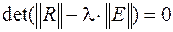которое для данного примера имеет вид

.

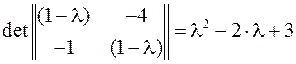Решение характеристического уравнения, полученного при раскрытии определителя, позволяет найти собственные значения 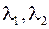являющиеся его корнями:

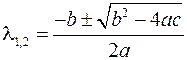
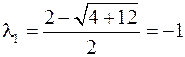
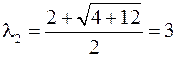
Для определения собственных векторов найденные собственные значения поочередно подставляются в систему уравнений

.

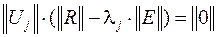При подстановке первого собственного значения 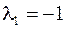данная система приобретает вид

,

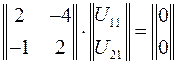то есть имеет место система линейно зависимых уравнений

.

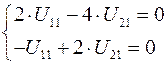В таком случае один из компонентов собственного вектора задается произвольно, например

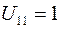
тогда

.

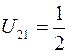Следовательно, первый собственный вектор

.

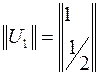При подстановке второго собственного значения 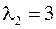имеет место система также линейно зависимых уравнений

.

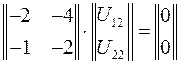
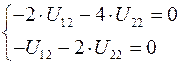При аналогичном задании одного из компонентов ( 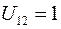) второй собственный вектор имеет вид

.

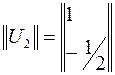В таком случае решение для переменных состояния

.

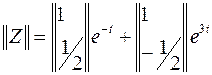
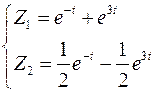Пусть переменные состояния – углы отклонения роторов от синхронной оси в энергосистеме с двумя генераторными узлами

.

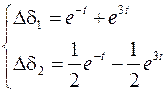Изменение во времени углов отклонения роторов генераторов от синхронной оси показаны на рис. 48. Наличие положительного действительного корня, как показано на рисунке, ведет к неограниченному росту углов отклонения, т.е. к апериодическому нарушению статической устойчивости.

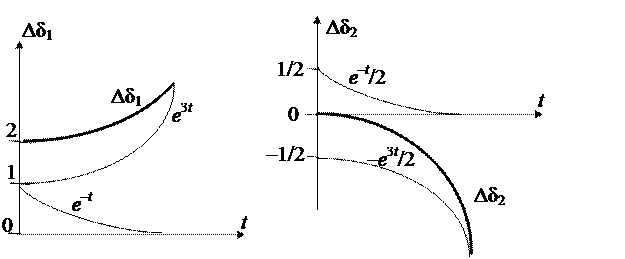
Рис. 48. Зависимости углов отклонения роторов генераторов от синхронной оси

Этапы модального анализа динамических свойств

сложных энергосистем

Динамические свойства энергосистемы определяются следующими параметрами:

1) частота электромеханических колебаний (ЭМК) ротора генератора 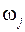, где ,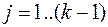

2) коэффициент затухания –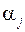

3) соотношение амплитуд колебаний роторов генераторов на частоте 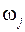, т.е. компоненты собственного вектора 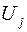, соответствующее данному собственному значению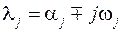

.

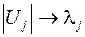Модальный анализ включает следующие этапы:

1. приведение математической модели энергосистемы к виду

;

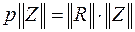2. вычисление собственных значений и собственных векторов матрицы энергосистемы 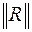из условий

;

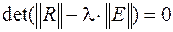
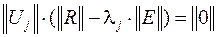3. выделение мод электромеханических колебаний, т.е. выделение из всей совокупности вычисленных собственных значений 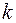пар комплексно сопряженных собственных значений соответствующих 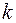модам электромеханических колебаний, где 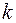– число синхронных машин;

4. выделение из полной модальной матрицы подматрицы собственных векторов соответствующих модам электромеханических колебаний

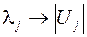
и выделение из указанных векторов элементов соответствующих углам отклонения роторов

,

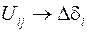что дает выделенную подматрицу размером ;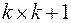

5. нормирование собственного вектора путем определения максимального по модулю элемента, на который делятся все остальные

.

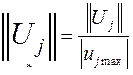Анализ мод электромеханических колебаний (ЭМК)

Существуют следующие виды мод ЭМК:

· Системные,

· Подсистемные,

· Локальные.

Вышеуказанные 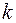пар комплексно сопряженных собственных значений дает спектр ЭМК, который по разному проявляется в режимных параметрах. Наиболее опасными являются низкочастотные слабозатухающие электромеханические колебания, которые охватывают всю энергосистему и проявляются в виде колебаний с наибольшей амплитудой во всех режимных параметрах. Следовательно, необходимо установить иерархию частот, выделив в первую очередь низкочастотные колебания. Для этого необходимо проанализировать компоненты собственного вектора выделенной подматрицы.

Иерархия мод определяется двумя признаками собственного вектора:

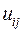– модуль собственного вектора,

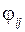– фаза собственного вектора.

Для отличия системных мод от локальных используются различия по модулю компонент собственного вектора. Если модули всех элементов собственного вектора лежат в диапазоне 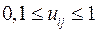, следовательно,мода системная. Если 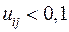для какого – либо i, то мода является локальной.

Для отличия системных мод от подсистемных используются различия по фазе собственного вектора.

Пусть имеется энергосистема, содержащая шесть генераторных узлов и такое же количество синхронных машин (см. рис. 49). Собственные значения и собственные вектора матрицы состояния данной энергосистемы приведены в табл. 2.

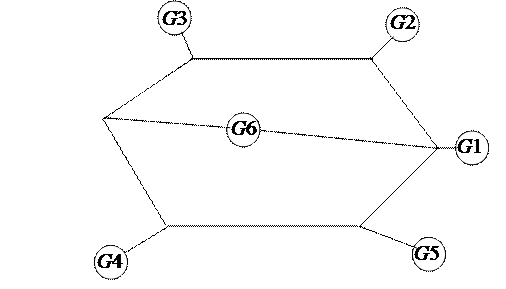
Рис. 49. Схема электрической сети, содержащей генераторные узлы

Табл. 2. Собственные значения и собственные вектора матрицы состояния энергосистемы приведенной на рис. 48.

Собственное значение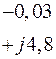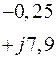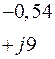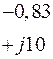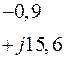
(частота), рад/с	4,8	7,9			15,6

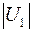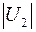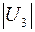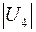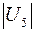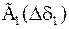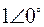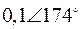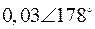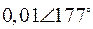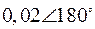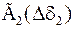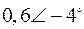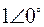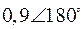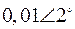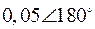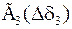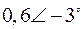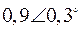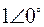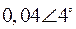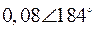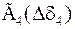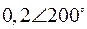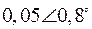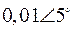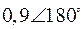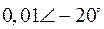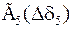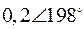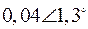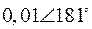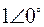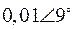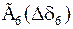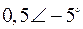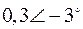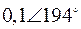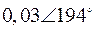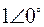Поскольку вещественные части всех собственных значений в рассматриваемом примере отрицательны, система является статически устойчивой.

Первая мода, соответствующая частоте 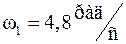, является системной, поскольку для всех модулей компонент ее собственного вектора верно 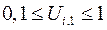. По признакам фаз элементов собственного вектора она разбивается на две подсистемные моды (см. рис. 50)

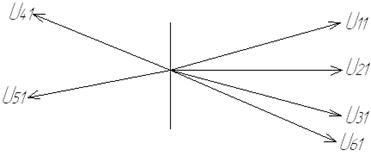
Рис. 50. Элементы собственного вектора системной моды

Вторая мода, соответствующая частоте 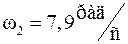, является локальной, поскольку два из шести компонент ее собственного вектора меньше десятой части максимального компонента, т.е. амплитуда колебаний роторов двух генераторов на данной частоте меньше десятой части амплитуды для второго генератора, для которого данная частота колебаний является собственной

,

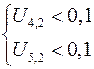по признакам фаз элементов собственного вектора данная мода также разбивается на две подсистемные.

Третья мода, соответствующая частоте 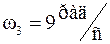, также является локальной, поскольку

.

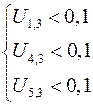Аналогично производится анализ остальных мод ЭМК.

Следующим этапом является проверка качества демпфирования. Демпфирование на частоте j-го ЭМК является удовлетворительным, если 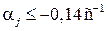и неудовлетворительным при 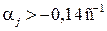. Как видно из табл. 2 для первой моды демпфирование неудовлетворительно, а для остальных мод (для всех j принадлежащих диапазону 2…5) 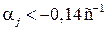и демпфирование удовлетворительно.

Первая мода вследствие ее низкочастотности проявляется во всей системе, но больше всего в режимных параметрах первого генератора, для которого ее частота является частотой собственных колебаний. Для получения удовлетворительного демпфирования необходимо повысить декремент затухания на системной частоте, т.е. подобрать настройки первого генератора таким образом, чтобы демпфировалась частота первой моды.

Каждой моде j-й электромеханических колебаний соответствует пара комплексно сопряженных собственных значений матрицы состояния энергосистемы

.

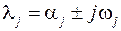Паре комплексно сопряженных собственных значений в свою очередь соответствует пара комплексно сопряженных собственных векторов (см. рис. 51)

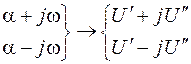
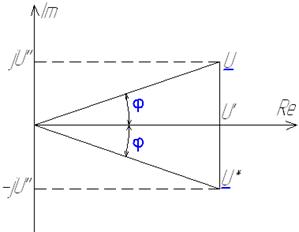
Рис. 51. Пара комплексно сопряженных собственных векторов

Как было показано выше решение для переменной состояния (в данном случае угла отклонения) записывается в виде

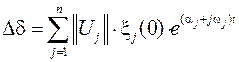
Каждому слагаемому этой суммы соответствует пара комплексно сопряженных собственных значений и пара комплексно сопряженных собственных векторов

.

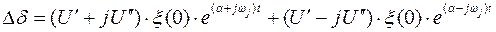Если записать данное выражение через показательные степени

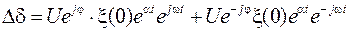
и вынести общие сомножители за скобки

,

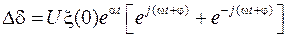то полученное уравнение соответствует уравнению гармонических колебаний

.

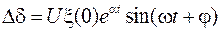Для рассматриваемого примера (см. табл. 2) угол отклонения ротора первого генератора можно также записать как сумму, каждое слагаемое которой соответствует частоте одной из мод ЭМК

.

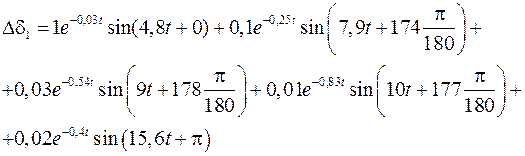Амплитуды трех последних мод на два порядка меньше системной, их демпфирование удовлетворительно, поэтому ими можно пренебречь.

Периоды ЭМК первой и второй мод соответственно

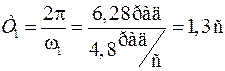
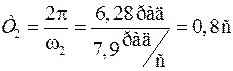
Декремент затухания первой моды α= –0,03 (что означает уменьшение амплитуды в e раз за 30 с, т.е. за 20 периодов), амплитуда колебаний с частотой первой моды для ротора первого генератора U₁₁=1, фаза φ₁₁=0.

Декремент затухания второй моды α= –0,25 (что означает уменьшение амплитуды в e раз за 4 с, т.е. за 5 периодов), амплитуда колебаний с частотой второй моды для ротора первого генератора U₁₂=0,1, фаза φ₁₂=174°.

ЭМК первой и второй мод для первого генератора рассматриваемого примера и их результирующая кривая показаны на рис. 52.

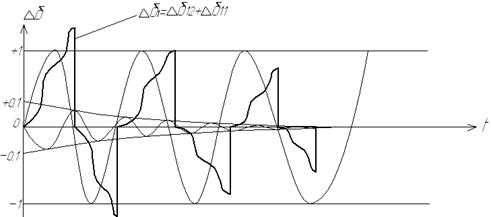
Рис. 52. Временная зависимость угла отклонения ротора генератора от синхронной оси

Приведение математической модели энергосистемы

к системе дифференциальных уравнений

первого порядка

Приведение математической модели энергосистемы к данной форме необходимо для модального анализа устойчивости. Дифференциальные уравнения любого порядка

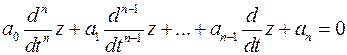
можно привести к дифференциальному уравнению первого порядка с помощью замен

,

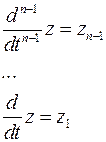в результате чего исходное уравнение приобретает вид

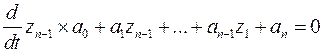
или же при введении оператора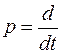

.

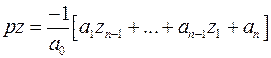Пусть энергосистема содержит три синхронных генератора, которые находятся, соответственно, в трех узлах электрической сети. Как показано в [9], в этом случае уравнения движения роторов генераторов имеют вид

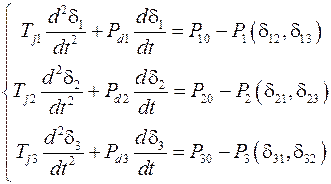
и мощности генераторов определяются из выражений

.

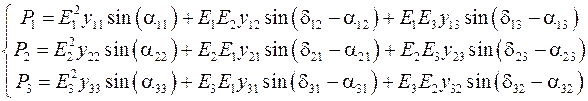Разложение уравнений движения роторов генераторов в ряд Тейлора без учета членов разложения, содержащих производные выше первой, дает систему уравнений

,

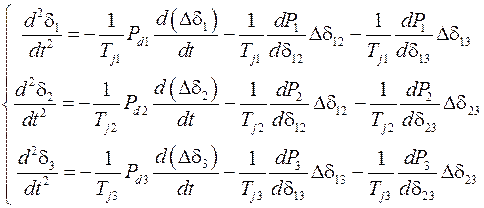где ,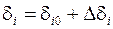

,

,

.

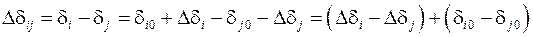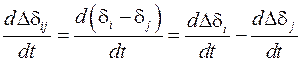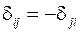При введении обозначений

,

,

,

,

,

,

,

,

,

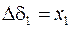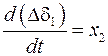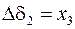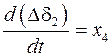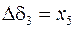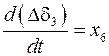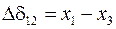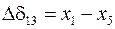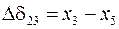число уравнений в системе удваивается, но они содержат производные только первого порядка

.

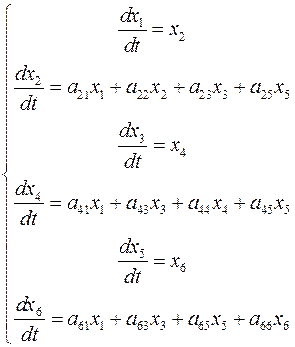Таким образом, система уравнений приведена к виду

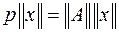
или же

,

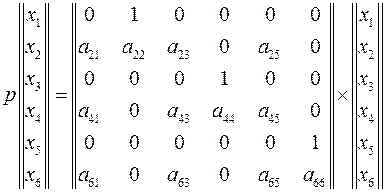где элементы матрицы состояния рассматриваемой энергосистемы определяются из выражений

,

,

,

,

,

,

,

,

,

,

,

.

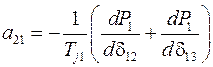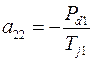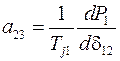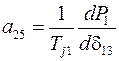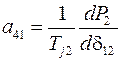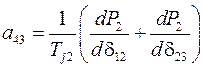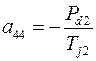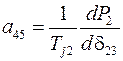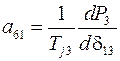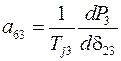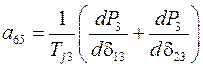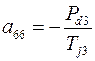Методы определения собственных значений

и собственных векторов матрицы состояния энергосистемы

Указанные методы делятся на два основных класса:

1) Методы определяющие по одному собственному значению и одному собственному вектору в одном интервале цикле:

a. Степенной метод;

b. Метод обратной матрицы,

2) Методы определяющие весь спектр собственных векторов и собственных значений в одном интервале цикле:

a. QR-алгоритм;

b. QL-алгоритм.

Степенной метод

Собственные значения 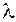и собственные вектора 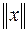квадратной матрицы состояния 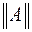удовлетворяют уравнению

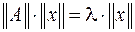
В начале первой итерации степенного метода произвольно задается начальное приближение первого собственного вектора 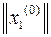соответствующего первому собственному значению матрицы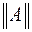

,

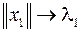причем начальное приближение должно быть ненулевым

.

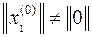Затем определяется следующее приближение собственного вектора по формуле

.

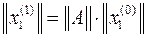Поскольку

,

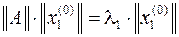следовательно

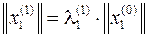
Для определения первого приближения собственного значения λ необходимо умножить обе части последнего уравнения на транспонированные столбцы начального приближения собственного вектора 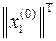(произведение строки и столбца дает число, что соответствует размерности собственного значения λ)

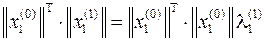
откуда

.

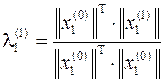Для степенного метода k-я итерация включает следующие этапы:

1. определение нового приближения собственного вектора

;

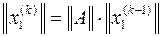2. определение нового приближения собственного значения

;

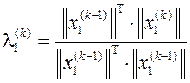3. проверка сходимости итерационного процесса

.

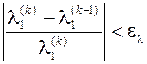Таким образом, k-е приближение собственного вектора 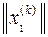представляет собой произведение его начального приближения 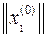на матрицу 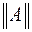в k-й степени

,

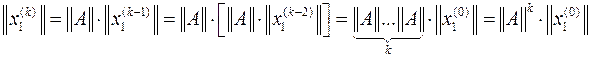откуда и название метода - степенной.

Степенной метод со сдвигом

Для определения второго собственного значения матрицы 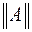, формируется матрица 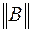, диагональные элементы которой сдвинуты относительно 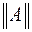на 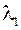, т.е.

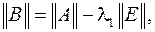
причем 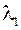вычисляется способом, описанным выше.

В итерационном цикле вычисляются 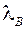– собственное значение матрицы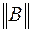

Для данного итерационного цикла каждый k-й шаг включает следующие этапы:

1) умножение матрицы 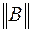на значение ее собственного вектора, найденного на предыдущей итерации

;

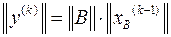2) определение нового приближения собственного значения матрицы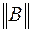

;

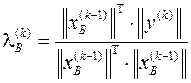3) Проверка сходимости

,

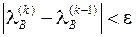где 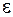– заданное число, характеризующее точность расчета;

4) Определение k-го приближения собственного вектора 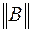делением столбца, найденного в первом пункте, на максимальный по модулю элемент данного столбца

.

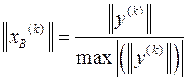После того, как в результате данного итерационного цикла с заданной точностью находится собственное значение 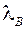матрицы 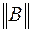, определяется следующее собственное значение матрицы 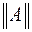по формуле

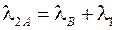
Для определения третьего собственного значения матрицы 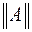формируется матрица 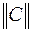со сдвигом диагональных элементов относительно 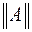на + .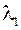

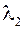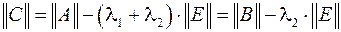
В результате итерационного цикла определяется 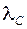– собственное значение матрицы 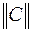и затем определяется третье собственное значение матрицы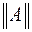

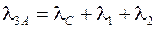
Таким образом, можно найти все или необходимое число собственных значений матрицы .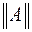

Пусть 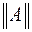представляет собой матрицу третьего порядка

,

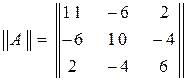а начальное приближение собственного вектора

.

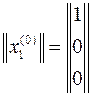Тогда первые приближения собственного вектора и собственного значения, вычисляемые в процессе первого итерационного шага

,

.

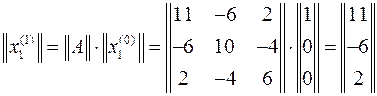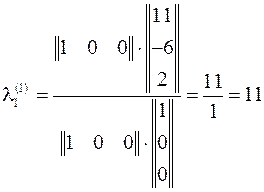Второй итерационный шаг степенного метода для данного примера имеет вид