Понятие об уклонениях отвесных линий
Физическая геодезия.
Глава 1
Понятие об уклонениях отвесных линий.
Изучение фигуры Земли тесно связано с уклонениями отвесных линий. Это явление вызвано отличием действительного гравитационного поля земли от нормального. Под нормальным полем Земли понимается гравитационное поле, создаваемое эллипсоидом вращения с равномерной плотностью масс. Существует два метода вывода уклонений отвесных линий: астрономо-геодезический и гравиметрический. Возможно сочетание этих методов. Рассмотрим первый из них.
Пусть в точке М местности (рис. 1) направление нормали к эллипсоиду обозначено через g, а направление отвесной линии через g.
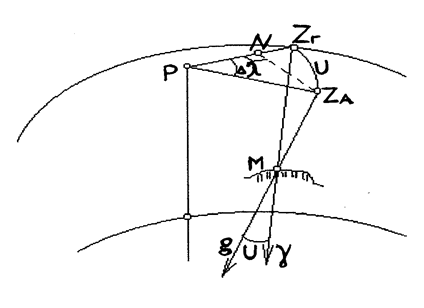 |
Угол U между этими направлениями называется полным уклонением отвесной линии. Это уклонение разлагается на две составляющие - по меридиану и по первому вертикалу. Для их вывода очертим вокруг точки М сферу и обозначим на ней точки: полюса Р, пересечения с ней отвесной линии ZА и пересечения нормали Zг. Точки ZА и Zг являются точками астрономического и геодезического зенитов.
РИС. 1
Опустим перпендикуляр с точки ZА на дугу PZГ и получим точку N. Угол в точке Р будет L - l, где
L - долгота меридиана дуги PZГ, а
l - долгота меридиана дуги РZА.
Дуга РZА равна 90°-j, а PZГ-(90°-B). Из прямоугольного сферического треугольника РZАN можно записать:
РN=(90°-j)*cos(L - l) (1)
Поскольку N лежит на меридиане, то составляющая уклонения на меридиане будет
NZГ=PZГ - PN
NZA=(90°-B)-(90°-j)*cos(L-l) (2)
Угол (L-l) мал, поэтому с достаточной для практических целей точностью можно записать:
NZA=(90°-B)-(90°-j)=j-B (3)
Обычно NZА обозначают через x, и тогда:
x=j-B (4)
Найдем теперь проекцию уклонения на первый вертикал, то есть дугу NZА.
Из теоремы синусов следует, что:
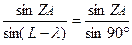 (5)
(5)
Обозначая NZА через h запишем:
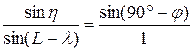 (6)
(6) 
Тогда:
sinh= cosj*sin(L-l) (7)
§2.Суть гравиметрического метода заключается в следующем:
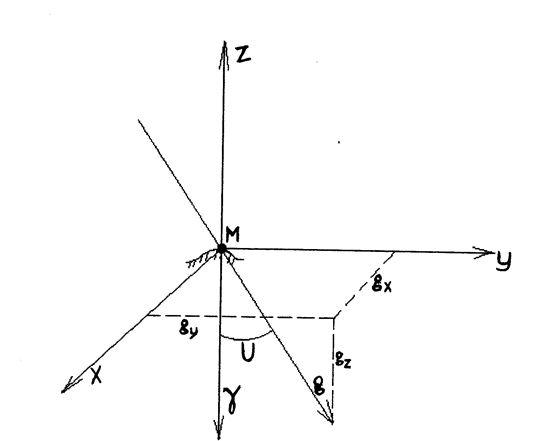 |
Введем в точке М систему координат, в которой ось Z направлена в зенит и совпадает с направлением нормали к эллипсоиду. Ось x направлена вдоль меридиана на север, а ось y вдоль первого вертикала.
РИС. 2
Направление вектора силы тяжести g разложим на три составляющие: gx, gy и gz. Тогда составляющие уклонения отвесных линий можно найти из следующих выражений:
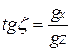 (8)
(8)
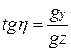 (9)
(9)
Выразим составляющие :gx, gy и gz через потенциал силы тяжести. Известно, что сила, действующая вдоль определенного направления равна производной потенциала по этому направлению, то есть:
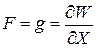 (10)
(10)
где: X - расстояние между притягивающим и притягиваемым телами. Тогда очевидно, что в пространственной системе координат:
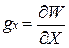 (11)
(11)
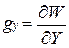 (12)
(12)
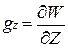 (13)
(13)
Выразим потенциал силы тяжести W через потенциал эллипсоида U и его отклонение T от потенциала силы тяжести, то есть запишем: W=U+T, (14)
Величину T ещё называют возмущающим потенциалом, а U - нормальным потенциалом.
Тогда очевидно, что
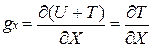 (15)
(15)
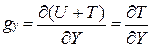 (16)
(16)
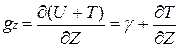 (17)
(17)
тогда:
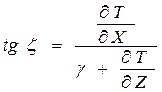 (18)
(18)
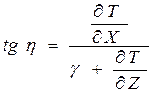 (19)
(19)
обозначая: dx=RdB
dy=RcosBdL
получим:
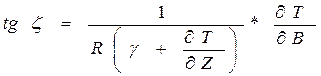 (20)
(20)
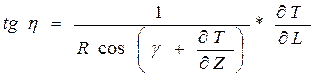 (21)
(21)
