Какие напряжения возникают в поперечных сечениях стержня при сдвиге?

Как уже отмечалось во введении, при смещении одного поперечного сечения относительно другого возникают касательные напряжения.

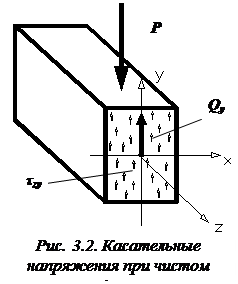Будем считать, что касательные напряжения распределены по всей площади поперечного сечения равномерно (рис. 3.2).

Тогда, если в поперечном сечении стержня площадью F возникает перерезывающая сила 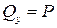, то касательные напряжения в любой точке этого сечения будут равны

.

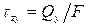Касательные напряжения 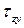измеряются в тех же единицах, что и нормальные напряжения 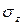: мегапаскалях, килоньютонах на квадратный сантиметр (МПа, кН/см²), а также в килограммах силы на квадратный сантиметр или миллиметр (кгс/см², кгс/мм²).

3.4. Как записывается закон Гука при сдвиге? Что называется модулем сдвига и в каких единицах он измеряется?

Опытным путем установлено, что в пределах упругой сдвиговой деформации касательные напряжения пропорциональны углу сдвига:

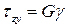. (3.1)

Соотношение (3.1) представляет собой закон Гука при сдвиге.

Коэффициент пропорциональности G в этой формуле называется модулем сдвига. Видно, что он измеряется в тех же единицах, что и касательное напряжение.

Модуль сдвига G является физической постоянной для материала, характеризующей его жесткость при сдвиге. Значение модуля сдвига G может быть определено экспериментально.

3.5. Какая зависимость существует между модулем сдвига и модулем Юнга?

Для изотропных материалов эта зависимость имеет вид:

.

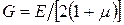Как уже отмечалось ранее, значение коэффициент Пуассона 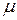лежит в пределах 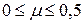. Следовательно,

.

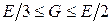Например, для стали любой марки:

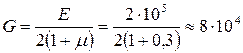МПа.

Аналогичное значение модуля сдвига для стали может быть получено в результате проведения эксперимента на сдвиг (или на кручение).

3.6. Как выглядит диаграмма 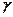– 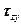при сдвиге?

Вид диаграммы 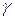– 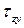аналогичен диаграмме 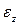– 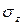при растяжении, которую мы рассматривали выше. Так, для пластичного материала на ней, в частности, имеются точки, характеризующие предел пропорциональности при сдвиге 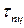, предел текучести 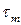, а также предел прочности 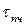. Последний соответствует срезу образца. Для многих материалов между пределом текучести при сдвиге 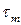и пределом текучести при растяжении 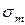существует следующая зависимость:

.

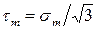3.7. Чему равна потенциальная энергия деформации при сдвиге?

Если участок стержня длиной 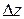испытывает чистый сдвиг, то накапливаемая в нем потенциальная энергия деформации определяется по формуле (подробнее см. беседу 15)

.

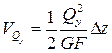3.8. Как записывается условие прочности при сдвиге?

Касательное напряжение, отвечающее безопасной работе материала при сдвиге, называется допускаемым напряжением и обозначается 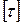. Для пластичных материалов оно должно быть меньше предела текучести :

,

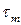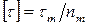а для хрупких материалов – меньше предела прочности :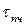

.

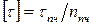Тогда условие прочности при сдвиге имеет вид:

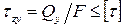. (3.2)

По формуле (3.2) осуществляется проверочный расчет соединений, работающих на срез.

Для определения требуемой площади поперечного сечения (проектировочный расчет) необходимо воспользоваться следующим неравенством, вытекающим из формулы (3.2):

.

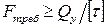3.9. Что такое срез? И как правильнее говорить «расчет на сдвиг» или же «расчет на срез»?

Под срезом обычно понимается непосредственное разрушение материала стержня, происходящее в результате деформации сдвига.

Под сдвигом понимается, собственно, угловая деформация или же вид напряженного состояния – чистый сдвиг.

Нам представляется, что, например, при проверке прочности соединений предпочтительнее говорить: «расчет на срез». Если же мы изучаем напряженное состояние, то правильнее говорить: «напряженное состояние при сдвиге».

3.10. В некоторых учебниках по сопротивлению материалов для модуля сдвига G встречаются и другие наименования, например, модуль упругости второго рода. Стоит ли использовать этот термин?

Употребление этого термина, как и другого термина «модуль упругости при сдвиге», которые, действительно, иногда можно встретить как в учебной литературе, так и в практике преподавания, мы бы не рекомендовали.

4. Геометрические характеристики
плоских сечений

Ранее мы установили, что прочность и жесткость стержня при растяжении и сжатии определяются площадью его поперечного сечения F:

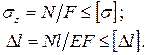
То есть, чем больше площадь поперечного сечения стержня, тем меньше возникающее в нем напряжение и меньше удлинение стержня.

Аналогично в условии прочности при сдвиге мы опять встречаемся с площадью поперечного сечения F:

.

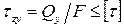Однако при других видах деформации, в чем мы убедимся в последующих наших беседах, площадь поперечного сечения уже не является той геометрической характеристикой, которая исчерпывающе определяет способность стержня сопротивляться внешней нагрузке.

Возьмем, например, обычную ученическую линейку и начнем ее изгибать. Мы легко убедимся в том, что если расположить линейку «ребром», то ее изгиб будет значительно меньше, чем в том случае, когда она будет расположена «плашмя».

Почему? Попробуем ответить на этот вопрос уже сейчас. При изгибе стержня его поперечные сечения поворачиваются вокруг некоторой оси (в дальнейшем мы узнаем, что эта ось называется нейтральной). И мерой сопротивления этому вращению, как нам известно из теоретической механики, является уже не площадь, а момент инерции поперечного сечения, который существенно зависит от высоты поперечного сечения.

Поэтому в настоящей беседе мы, отвлекаясь от физических свойств материала, и изучим некоторые геометрические характеристики поперечного сечения стержня, которые определяют его способность сопротивляться другим видам деформации, в частности, изгибу и кручению.

4.1. Что называется статическим моментом площади поперечного сечения относительно некоторой оси?

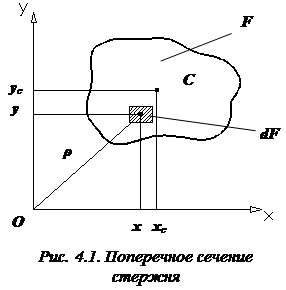Рассмотрим произвольную плоскую фигуру (поперечное сечение стержня) площадью F. Проведем через произвольную точку О оси координат x и y.Выделим элемент площади 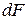с координатами x и y (рис. 4.1).

По аналогии с понятием момента силы относительно оси введем понятие статического момента (или просто момента) площади фигуры относительно оси.

Величину, равную произведению площади 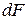на расстояние y до оси x (иными словами, произведение элементарной площади на плечо), назовем статическим моментом элемента площади относительно оси x:

.

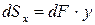По аналогии статический момент элемента площади 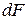относительно оси y будет равен:

.

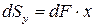Просуммировав такие произведения по всей площади F, мы получим статические моменты площади всей фигуры относительно осей x и y соответственно:

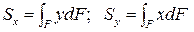. (4.1)

Статический момент площади фигуры относительно оси измеряется в единицах длины в кубе (как правило, в см³). Он может быть положительным, отрицательным и, как мы увидим в дальнейшем, равным нулю.

Пусть 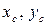– координаты центра тяжести фигуры. Продолжая аналогию с моментом силы, можно записать следующие выражения:

. (4.2)

Таким образом, статическим моментом площади фигуры относительно оси называется произведение площади фигуры на расстояние от ее центра тяжести до этой оси.

4.2. Как определить координаты центра тяжести поперечного
сечения стержня?

Из формул (4.2) следует, что статический момент площади фигуры относительно центральной оси (то есть оси, проходящей через центр тяжести фигуры) равен нулю.

Сопоставляя (4.1) и (4.2), мы легко получим формулы, позволяющие определить положение центра тяжести поперечного сечения стержня:

. (4.3)

Если площадь всей фигуры можно разбить на n простых частей, для которых известны и площадь 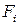, и положение центра тяжест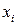и и 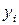, то вместо формул (4.3) мы получим:

.

4.3. Что называется осевым, полярным и центробежным моментами инерции фигуры? В каких единицах они измеряются?

Осевым моментом инерции площади фигурыназываетсяинтеграл произведений элементарных площадей на квадраты их расстояний до
рассматриваемой оси. Так, моменты инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y соответственно равны:

. (4.4)

Полярным моментом инерции площади фигуры относительно данной точки (полюса) называется интеграл произведений элементарных площадей на квадраты их расстояний до полюса:

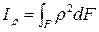. (4.5)

Если через полюс проходят две взаимно перпендикулярные оси x и y, то 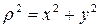. И тогда

.

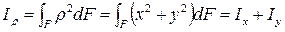Из формул (4.4) и (4.5) видно, что значения осевых и полярного моментов инерции всегда положительны, поскольку координаты 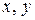и расстояние 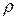входят в них в квадрате.

Центробежным моментом инерции площади фигуры называетсяинтеграл произведений элементарных площадей на их расстояния до осей x и y:

.

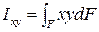Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см⁴).

Понятие о моменте инерции впервые ввел в науку в 1673 г. французский ученый Христиан Гюйгенс (Huygens, 1629 – 1695 гг.).

4.4. Какие оси называются главными осями?

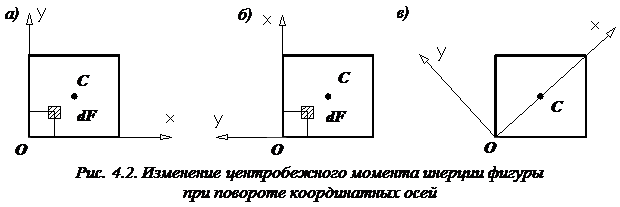
В зависимости от положения координатных осей центробежный момент инерции может быть положительным, отрицательным, а также равным нулю. Рассмотрим, например, квадрат (рис. 4.2, а).

Центробежный момент инерции квадрата 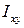относительно осей 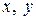положителен, так как координаты 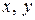у всех элементов площади положительные. При повороте осей вокруг начала координат на угол 90⁰
(рис. 4.2, б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны.

Очевидно, что можно найти такое положение двух взаимно перпендикулярных осей 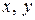, при котором 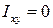. Такие оси называются главными осями. Для квадрата такие оси изображены на рис. 4.2, в.

Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ось перпендикулярна ей).

Главные оси, проходящие черезцентр тяжести поперечного сечения стержня, называются главными центральными осями.

Понятие о главных осях впервые введено в 1755 г. Яношем Сегнером (Segner, 1704 – 1777 гг.) и, независимо от него, в 1758 г. Леонардом Эйлером (Euler, 1707 – 1783 гг.).

Заметим, что иногда главные оси называют главными осями инерции. Автор рекомендует пользоваться первым определением, поскольку термин инерция к осям не имеет никакого отношения.

4.5. Какие моменты инерции называются собственными?

Осевые и центробежный моменты инерции относительно осей, проходящих через центр тяжести поперечного сечения стержня, иногда называются собственными моментами инерции.

4.6. По какой формуле вычисляются моменты инерции фигуры относительно оси, параллельной центральной? Какие моменты инерции называются переносными?

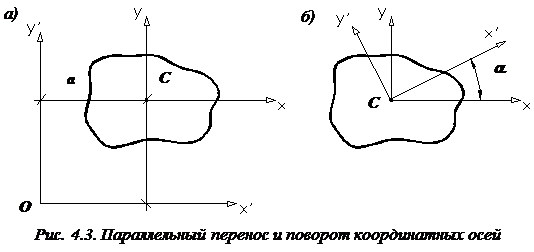
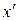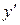Пусть две взаимно перпендикулярные оси x и y проходят через центр тяжести C поперечного сечения стержня. Проведем другие оси координат и , параллельные осям x и y. Обозначим a и b координаты центра тяжести С в новых осях 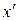и 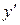(рис. 4.3, а).

Тогда осевые и центробежный моменты инерции фигуры относительно новых осе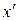й и 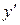будут определяться по следующим формулам:

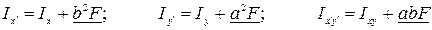. (4.6)

Очень часто эти формулы необоснованно приписывают немецкому ученому Якобу Штейнеру (Steiner, 1796 – 1863 гг.). Однако на самом деле они были доказаны еще в 1749 г. Эйлером.

Первые слагаемые в формулах (4.6) ранее нами были названы собственными моментами инерции. Вторые (подчеркнутые) слагаемые в этих формулах называются переносными моментами инерции.

Отметим, что координаты a и b подставляются в формулы (4.6) с учетом их знаков, что является крайне важным, в частности, для третьей из этих формул.