Математический маятник

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжёлый шарик, подвешенный на тонкой длинной нити.

На невесомой нити длиной l подвешен груз массой m, совершающий колебания относительно положения равновесия. Нулевое значение потенциальной энергии выбрано в точке равновесия, тогда в произвольном положении

U = mgh = mgl(1 – cos θ), (18)

где угол отклонения маятника от положения равновесия θ однозначно определяет положение груза в любой момент времени. Как было показано, уравнение второго закона Ньютона в случае движения по окружности принимает вид: .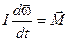

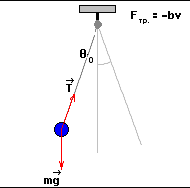
Рисунок 1 Математический маятник

Вектор 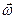направлен вдоль оси z (если принять плоскость качаний маятника за плоскость (x,y)). Момент инерции точки на окружности равен

I = ml². Соответствующая проекция момента силы тяжести относительно оси, проходящей через точку подвеса, равна М = –mglsinθ. Поэтому уравнение колебаний маятника принимает вид:

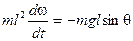(19)

Так как угловая скорость ω = dθ/dt, то окончательно

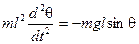(20)

Это уравнение точное, однако его решение сложно. Представим теперь, что маятник совершает малые колебания. В этом случае θ << 1 и можно сделать замену: sinθ ≈ θ. Уравнение малых колебаний математического маятника приобретает вид уравнения для гармонического осциллятора:

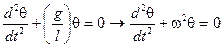, (21)

где введено обозначение ω = (g/l)^1/2. Этой формулой определяется частота колебаний математического маятника. Период колебаний математического маятника равен

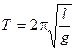. (22)

Методика измерений

Период малых колебаний физического маятника равен

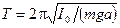(23)

где I₀ — момент инерции маятника относительно оси качаний ОO, m - масса маятника, а - расстояние от оси качаний маятника до его центра масс, g — ускорение свободного падения

В данной работе проводится экспериментальная проверка соотношения (23) в случае, когда маятник можно приближенно считать математическим, т. е. когда масса маятника сосредоточена в области, размеры которой малы по сравнению с а.

Исследуемый в лабораторной установке маятник схематически изображен на рисунке 2. Он представляет собой стальной шарик радиусом r на бифилярном подвесе: тонкая нить пропущена через центр шарика, концы нити закреплены на стойке. Длина подвеса может регулироваться в пределах от нескольких сантиметров до 1 м. Период колебаний с высокой (до 10^-3 с) точностью измеряется с помощью электронного секундомера.

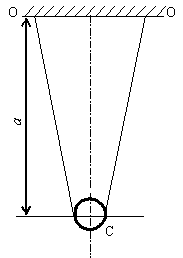
Рисунок 2 Принципиальная схема математического маятника

Момент инерции маятника складывается из момента инерции шарика и момента инерции нити подвеса. Пренебрегая моментом инерции нити, запишем момент инерции маятника относительно оси 00 в виде

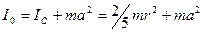(24)

Соотношение (24) следует из теоремы Гюйгенса—Штейнера, если учесть, что момент инерции однородного шара радиусом r и массой m относительно оси, проходящей через его центр, равен

I_С=2/5mr².

Рассмотрим случай, когда радиус шарика мал по сравнению с длиной подвеса: r << а. Тогда в (24) можно пренебречь слагаемым 2/5mr², малым по сравнению с mа², и положить

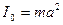. (25)

В этом приближении I₀ определяется, очевидно, с небольшой си­стематической погрешностью

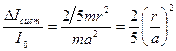(26)

которую в условиях опыта легко оценить. С учетом (25) период колебаний маятника можно записать в виде

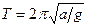(27)

Он, как и должно быть, совпадает с периодом колебаний математического маятника, длина подвеса которого а. Из (27) находим следующее выражение для ускорения свободного падения:

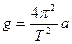(28)

Соотношение (28)позволяет опытным путем определить ускорение свободного падения. Для этого, очевидно, необходимо измерить период колебаний маятника Т и длину подвеса а, затем рассчитать g по формуле (28).

Однако, прежде чем перейти к определению g, необходимо выяснить, применимо ли вообще соотношение (28) для лабораторной установки.

Дело в том, что выражение (23)для периода колебаний справедливо для идеализированной модели физического маятника. Следовательно, и соотношение (28)также справедливо только в рамках этой модели. При выводе соотношения (23)были сделаны следующие предположения :

1) маятник совершает колебания малой амплитуды, и поэтому период колебаний не зависит от амплитуды (изохронность колебаний);

2) затуханием колебаний можно пренебречь.

Непосредственным измерением легко проверить, что периоды колебаний маятника при малой (порядка 3—5°) и большой (30—45°) амплитудах заметно отличаются. Так как расчетная формула (28)применима только для малых амплитуд, то необходимо определить, в каком диапазоне амплитуд период колебаний остается постоянным с достаточно высокой точностью (например, с точностью до 0,5%). Это легко сделать, измеряя период колебаний маятника для различных значений амплитуды в пределах от 2—3° до 10—15°.

Обсудим теперь, как можно оценить влияние затухания на период колебаний маятника. Отклонив маятник из положения равновесия, легко проверить, что колебания его постепенно затухают. Количественную оценку величины поправки ΔТ к периоду можно получить, если учесть, что основной причиной затухания колебаний маятника является вязкое трение о воздух.

В этом случае действующая на шарик сила трения пропорциональна скорости его движения:

F_тр= - bυ, b >0.

Период колебаний маятника несколько увеличивается, а частота колебаний уменьшается по сравнению с частотой маятника без трения. При этом частота колебаний

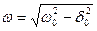(29)

а их период

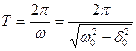(30)

где .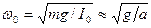

Коэффициент затухания выражается через число колебаний N, за которое амплитуда колебаний уменьшается в е = 2,78 ≈ 3 раза:

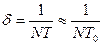(31)

Из соотношений (29), (30) и (31)находим

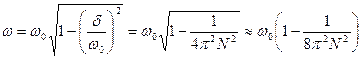(32)

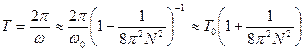(33)

Таким образом,

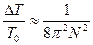(34)

Видно, что уже при N ≈ 10 поправка (34) к периоду колебаний

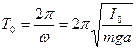
меньше 0,1% и ею можно пренебречь.