Билет.Колебательное звено 2-го порядка

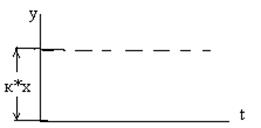
Билет.Безынерционное звено (усилителительное)

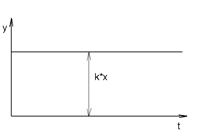
Динамическая характеристика имеет вид:y=k x

Преобразуем уравнения по Лапласу y(p)=k x(p); W(p)=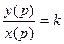

Пример данного звена- n-регулятор, все усилители,рычаги.

34билет.Инерционное звено (апериодическое звено 1-го порядка)

Динамическая характеристика такого звена имеет вид: T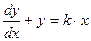

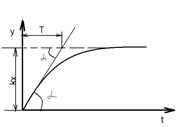
T-постоянное времени, к-коэф. усиления; x-const;

y= 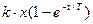построим графики переходного процесса:

; ;

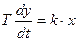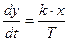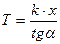
Для этого преобразуем по Лапласу: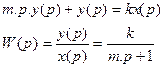

Одноемкостные статические обьекты: термопары, мембрано-исполнительный механмзм .Данное звено называется аппериодическим звеном 1-го порядка.

Билет.Интегрирующее звено

Динам хар-ка: Т*dy/dt=к*х , Преобразуем: dy/dt=к*х/Т, 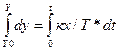, Проинтегрируем: y-y0=к/Т* 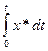, х=cоnst, y=кх/Т*t+y0

График переходного процесса:

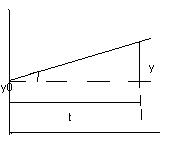
y/t=кх/Т=tgα, α=аrctgк*х/Т. Получим ф-циюзвена, преобразуем по Лапласу:

Т*р*y(р)=к*х(р), W(р)=y(р)/х(р)=к/Т*р. Данное звено наз астатическим звеном 1-го порядка (емкостные астатические объекты, интеграл регуляторы).

Билет.Дифференцирующее звено

Они дел-ся на реальные и идеальные. Динам хар-ка идеал диф звена имеет вид:

y=к*dх/dt (При t=0, y 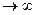; при t 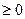, у=0)

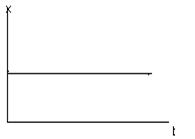
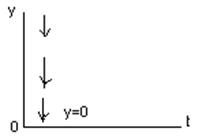
Пол-чим передаточную ф-цию звена: у(р)=к*р*х(р), W(р)=у(р)/х(р)=к*р

Пример:

1. Эл контур, в котором протекает ток и им-ся напряжение, тогда ток в контуре будет равен: i=c*dUвых/dt

2. Трансформеры напряжения: Uвых=к*dФ/dt, Ф=к1*i1 (величина потока созд-ся в сердечнике i1). Uвых=к2*di1/dt (вых напряжение).

Динам хар-ка реал диф звена им вид: Т*dy/dt+y=k*dx/dt (при t=0, y , при t , y=k*x*e^-t/T

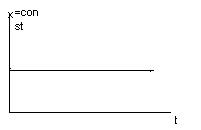
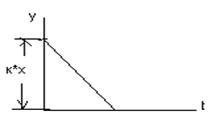
Получим передаточную ф-цию: Т*р*у(р)+у(р)=к*р*х(р), W(р)=к*р/(Т*р+1).

Пример: Эл контур, содержащий емкость с и сопративление R. Получим: R*c*Uвых/dt+Uвых= dUвых/dt – закон Киркгофа. Диф. звенья широко применяются в АСР и способствует устойчивой ее работе.

билет.Колебательное звено 2-го порядка

Это такое звено, у которого при скачкообразном изменении х,выходная величинана – у изменится в колебательном режиме с постоянным периодом и с амплитудой затухающего колебания по экспоненте. Динамическая характеристика имеет вид:

Т0²*d²y/dt²+T*dy/dt+y=к*х. Это уравнение 2-го порядка, звено имеет 2 емкости – Т0 и Т. Для решения уравнения необходимо получить передаточную функцию и характерное уравнение для данного звена. Передаточная функция:

Т0²*р0²*у(р)+Т*р*у(р)+у(р)=к*х(р)

W(р)=у(р)/х(р)=к/(Т0²*р²+Т*р+1). Характерное уравнение (когда знаменатель=0): Т0²*р²+Т*р+1=0.

Найдем корни: Р1,2=-Т/(2*Т0²)± 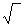(Т²-4Т0²/4*Т0⁴). Данные корни могут быть комплексно-сопряженные или действительно отрицательные. Если Т<2Т0, то корень дифференциала уравнения будет отрицательным и корни комплексно-сопряженные, т е: Р1,2=-α±j*ω. Коэффициент затухания α=Т/2Т0², ω= 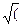4Т0²/Т0/4Т0⁴) – частота вынужденных колебаний выходной величины у. Решение будет иметь вид: у=у установится – с*е^-αt*sin(ω*t+ψ), где с, ω – постоянные интегрирования, которые определяются из начальных условий, т е: (dy/dt)_t=0. Параметры: у установится = к*х, с=к*х*(ω0/ω), ω0=1/Т0 – частота свободных колебаний выходной переменной, ψ=arctg(ω/α). Подставив все получим:

y=кх*[1 - ω0/ω*е^-αt*sin(ω*t+arctg ω/α)]. График переходного процессса (х=const):

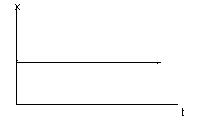
Пример: двухъемкостные статические объекты, электродвигатели переменного тока (асинхронные).