Отношение порядка и решетка

R ⊆ A × A есть отношение нестрогого частичного

порядка, если и только если оно

• рефлексивно

• антисимметрично

• транзитивно

В таком случае A называют частично-упорядоченным

множеством и обозначают через ( A, ≥ )

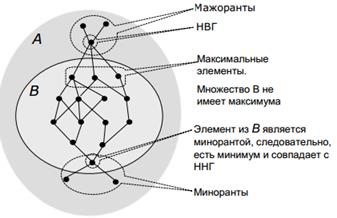
Пусть дано ( A, ≥ ) и В ⊆ А. Тогда а из А есть

мажоранта множества В, если для всех b из B

справеливо утверждение a ≥ b.

Миноранта. Максимум. Минимум. НВГ

Пусть дано ( A, ≥ ) и В ⊆ А. Тогда а из А есть

миноранта множества В, если для всех b из B

справеливо утверждение b ≥ a.

Если мажоранта принадлежит B, то она называется

максимумом множества B.

Если миноранта принадлежит B, то она называется

минимумом множества B.

Как легко показать, при условии существования

максимум (минимум) единственен.

Если множество всех мажорант в свою очередь имеет

минимум, то этот элемент единственен и его называют

наименьшей верхней гранью (НВГ) и обозначают Sup B.

НВГ и ННГ. Решётка.

Другое определение НВГ:

Пусть дано ( A, ≥ ) и В ⊆ А. Тогда а из А есть НВГ

множества В, если и только если

1) a ≥ b для всех b ∈ B

2) Если a’ ≥ b для всех b ∈ B и a’ ≠ a, то a’ ≥ a.

Если множество всех минорант в свою очередь имеет

максимум, то этот элемент единственен и его называют

наибольшей нижней гранью (ННГ) и обозначают Inf B.

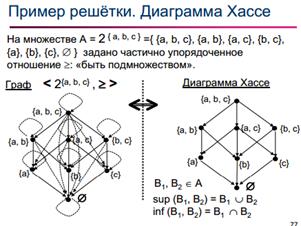
Решетка есть частично упорядоченное множество

L = ( A, ≥ ), для любых двух элементов которого

найдется НВГ (supremum)и ННГ (infimum).

Линейный порядок. Строгий порядок.

Если отношение R удовлетворяет условию

дихотомии (для любых a и b из A справедливо либо

a R b , либо b R a), то такое отношение называется

линейным порядком.

Если отношение асимметрично (антисимметрично и

антирефлексивно) и транзитивно, то оно называется

строгим порядком ( A, > ).

Бинарная операция (bi — два) — математическая операция, принимающая два аргумента и возвращающая один результат (то есть с арностью два).

Пусть ψ-бинарная операция

Для a, b ∈ M запись ψ(a, b) равносильна a ψ b

Операция ψ называется ассоциативной, если для любых a, b, c ∈ M (a ψ b) ψ c = a ψ (b ψ c).

Операция ψ называется коммутативной, если a ψ b = b ψ a

Множество М* ⊆ М замкнуто относительно операции ψ ,если и только если для любых a, b ∈ M*

верно, что a ψ b ∈ М*

Если ψ и ϕ есть две бинарные операции на М , то ψ называется дистрибутивной относительно ϕ ,если a ψ (b ϕ с) = (a ψ b) ϕ (a ψ с) Наряду с несущим множеством и набором операций

конкретная алгебра определяется совокупностью специальных констант. Элемент е такой, что для любого a ∈ M a ψ e = e ψ a = a называется нейтральным элементом (единицей).

Элемент z (константа) такой, что для любого a ∈ M a ψ z = z ψ a = z называется нулём.

Элемент а ^-1 назывется обратным к элементу а относительно операции ψ, если а ψ а^-1= е

Дизъю́нкция (лат. disjunctio — разобщение), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».

Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И",логи́ческое умноже́ние, иногда просто "И".

Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.

Вот так выглядит элемент «И» и его таблица истинности:

Булевой алгеброй[1][2][3] называется непустое множество A с двумя бинарными операциями 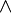(аналог конъюнкции), 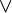(аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:

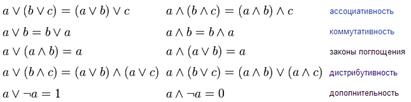
Первые три аксиомы означают, что (A, 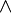, 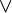) является решёткой. Таким образом, булева алгебра может быть определена как дистрибутивная решётка, в которой выполнены две последние аксиомы

Коммутативная операция

Бинарная операция называется коммутативной, если её результат не зависит от перестановки операндов, то есть

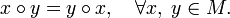
Ассоциативная операция

Бинарная операция называется ассоциативной, если

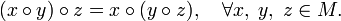
Для ассоциативной операции результат вычисления 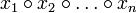не зависит от порядка вычисления (расстановки скобок), и потому позволяется опускать скобки в записи. Для неассоциативной операции выражение 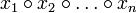при 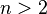однозначно не определено.

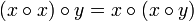Бинарная операция называется альтернати́вной если

и .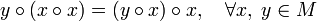

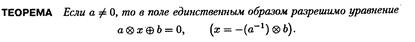
Изоморфизм

Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называютсяизоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.

Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными.

Гоморфизм

Гомоморфный образ — образ математического объекта, имеющего структуру полугруппы, группы, кольца, алгебры при гомоморфном отображении. Иногда говорят и о гомоморфных образах других математических объектов, например, графов.

ГРАФЫ

Лекция 11

Графы

Графом (G) будем называть тройку объектов (V, X, ?))

V – множество n вершин.

X – конечное множество ребер.

? - функция инцидентности, которая каждому элементу множества X ставит в

соответствие пару элементов из множества V.

? задана на множестве X.

Если в значении функции инцидентности допускается перестановка вершин, то

граф называется неориентированным. В противном случае граф называется

ориентированным (Орграф).

Vj – начало ребра

Vk – его конец

?(xi) = (Vj, Vk) – ребро инцидентно в вершине Vj и в вершине Vk.

Если одной и той же паре вершин инцидентно несколько ребер, то ребра

называются кратными.

Если на ребре xi0

?((x0) = (Vj0, Vj0),

то ребро называется петлей.

Способы задания графов

1. Аналитический

Если вершине не инцидентно никакое ребро, то эта вершина называется

изолированной.

Выписываются все ребра и пишутся напротив две пары вершин, которым они

инцидентны.

В конце выписываются все изолированные вершины.

2. Геометрический

Каждая вершина графа задается точкой. А ребра, инцидентные паре вершин –

кривой.

Желательно рисовать кривые без пересечения. Если пересечения существуют, то

их надо отличать от вершин.

3. С помощью матрицы инцидентности

A(m*n)

m = [V] – число вершин

n = [X}- число ребер

а) Неориентированные графы

Aij = {0, если Vi не инцидентно xj, 1, если Vi инцидентно xj)

б) Орграфы

Aij = {0, если Vi не инцидентно xj, -1, если Vi - начало xj, 1, если Vi -

конец xj)

Для петель нужны дополнительные предположения.

4. Матрица смежности (задается одинаково для всех графов)

B(m*m) m = [V]

Bij равно числу ребер, инцидентных паре вершин (oi, oj)

Если граф не ориентирован, то матрица симметрична.

Граф, в котором нет кратных ребер и петель, называется простым.

Простой граф называется полным, если любой паре его вершин инцидентно одно

ребро.

Дальше все о неориентированных графах.

K1 – полный граф с одной вершиной

K2 – с двумя

K3 – с тремя

K4 – полный граф с четырьмя вершинами

K5 – полный пятивершинник

Граф называется двудольным, если множество вершин разбивается на 2

непересекающихся подмножества, такие, что ребра соединяют вершины из разных

подмножеств.

Двудольный граф называется полным, если каждая вершина одного подмножества

соединена ребром с каждой вершиной другого подмножества.

Полный двудольный граф.

Маршруты, циклы, связности.

Маршрутом в графе называется чередующаяся последовательность вершин и

ребер, начинающаяся и заканчивающаяся вершинами, такую, что каждое ребро в

нем соединяет только те вершины, между которыми оно стоит.

Будем говорить, что этот маршрут соединяет первую и последнюю вершину. Если

существует маршрут, то последняя вершина называется достижимой из первой

вершины.

Маршрут, в котором нет повторяющихся ребер, называется цепью.

Маршрут, в котором нет повторяющихся вершин (кроме первой и последней),

называется простой цепью.

Если в простой цепи первая и последняя вершины совпадают, то она называется

циклом.

Граф называется связным, если любая вершина достижима из любой другой

вершины. В противном случае граф называется несвязным. Несвязный граф

распадается на несколько частей, каждая из которых является связным графом.

Эти части называются компонентами связности.

Ребро называется циклическим, если оно входит хотя бы в один цикл графа. В

противном случае ребро называется ациклическим.

Утверждение.

Если из связного графа удалить циклическое ребро, то вновь полученный граф

останется связным, а если удалить ациклическое ребро, то граф распадется на

два компонента связности.

Связный граф, у которого все ребра ациклические, называется деревом.

Несвязный граф, компонентами связности которого являются деревья, лесом.

Свойства деревьев.

1. Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы

число вершин было больше числа ребер на один.

2. Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины

его соединялись единственным маршрутом.

3. Граф будет деревом тогда и только тогда, когда добавление любого нового

ребра приводит к появлению ровно одного цикла.

Лекция 12

Эйлеровы графы

Дан граф. Требуется найти в нем маршрут, проходящий по каждому ребру ровно

один раз. Начало и конец – в одной вершине.

Такой маршрут называется Эйлеровым циклом, а граф, в котором он существует,

называется Эйлеровым графом.

Степень вершины в графе – это число ребер, инцидентных этой вершине.

Критерий эйлеровости графа.

Для того, чтобы связный граф без петель был Эйлеровым, необходимо и

достаточно, чтобы степень его вершины была четным числом.

Планарные графы.

Определение.

Укладкой графа называется такое его геометрическое изображение, при котором

ребра пересекаются только в вершинах. Если существует укладка графа на

плоскости, то граф называется планарным.

Сама же укладка графа без пересечения ребер называется плоским графом.

Любой граф можно изобразить в трехмерном пространстве без пересечения

ребер.

Для любого графа xi, соединяющего 2 вершины проводим новую плоскость,

содержащую эту прямую, а ребро рисуем на плоскости.

Граф будет планарным, если существует его укладка на сфере.

Доказательство следует из взаимно однозначного соответствия точек на сфере

с точками плоскости из стереографических проекций.

Следствие. Граф любого выпуклого многогранника планарен.

Ребра плоского графа разбивают плоскость на несколько частей, одна из

которых бесконечна. Эти части и являются гранями плоского графа.

Теорема Эйлера о плоских графах.

Формула Эйлера.

Для плоского графа справедливо соотношение.

M – N + P = 2.

Докажем индукцией по числу граней

P = 1

Если P = 1, то граф – дерево. В нем нет ни одного цикла. У дерева число

вершин больше числа ребер на 1.

M = N + 1

N + 1 – N + 1 = 2 – справедливо.

Пусть p = k, и утверждение верно.

Тогда оно верно и при P= k+1

Берем ребро графа, отделяющее бесконечную грань от внутренних и удаляем это

ребро из графа. Т.к. оно циклическое, то в новом графе g1 (он также будет

связным) число вершин M останется прежним.

N1 = N – 1

P1 = P – 1

M = M

k + 1-1 = k

Для g1 справедливо предположение индукции.

M1 + N1 + P1 = 2

M – N – 1 + K = 2

M – N + K – 1 = 2

M – N + P = 2

Что и требовалось доказать.

Следствие 1.

Для плоского связного простого графа справедливо соотношение

n <= 3*(m-2)

Следствие 2.

Для плоского связного простого графа без треугольных граней справедливо

соотношение

n <= 2*(m-2)

Следствие 3.

Граф K5 – непланарен.

m > 2

И если бы он был плоским, то для него было бы справедливо следствие 1.

N <= 3*(m-2)

10 <= 9 – неверно.

Противоречие. Значит, он не может быть нарисован плоским.

Следствие 4.

Граф K3-3 непланарен.

Нет треугольных граней.

Если бы он был плоским, то для него было бы справедливо следствие 2.

9 <= 2*(6-2)

9 <= 8 – неверно.

Противоречие из предположения, что он не может быть плоским.

Операцией разбиения ребра графа называется следующая процедура:

Ребро удаляется из графа, и в граф добавляется новая вершина, соединенная

новыми ребрами с концами данного ребра.

Два графа называются гомеоморфными, если каждый из них может быть получен

из одного и того же графа путем применения конечного числа раз операции

разбиения ребер.

Теорема Понтрягина – Куратовского.

Чтобы граф был планарным, необходимо и достаточно, чтобы он не содержал

гомеоморфных подграфов.

Лекция 13

Сети. Пути в орграфах. Остовы минимальной длины

Определение. Двуполюсной сетью называется связный граф без петель с двумя

выделенными вершинами, которые называются полюсами.

Двуполюсная сеть называется сильно связанной (связной), если через любое

ребро проходит простая цепь, соединяющая полюса. В ней нет повторяющихся

вершин.

Параллельная сеть – сеть вида

Последовательная сеть – сеть вида

П (пи) сети – последовательно-параллельные сети

Примеры П-сетей

Такая сеть называется мостиковой.

Контактными схемами называются сильносвязные двуполюсные сети, каждому

ребру которой поставлено в соответствие x или NOT(x).

X Not Y

Z Not X

Любой контактной схеме (КС) можно поставить в соответствие булеву функцию

(функцию проводимости) по правилу:

Для любой простой цепи, соединяющей полюса, записываем ЭК тех переменных,

которыми помечены ребра этой цепи.

Затем берем дизъюнкцию всех ЭК. Получим искомую функцию проводимости.

Если в контактной схеме будут стоять переключатели (релейные контакты),

которые будем считать замкнутыми, если выражение, стоящее у ребра равно 1

или в противном случае разомкнутыми, то при подаче на полюса разности

потенциалов (электрического тока) контактная схема будет проводить ток при

таких и только при таких состояниях контактов, при которых значение функции

равно 1.

Минимальной контактной схемой для функции называется контактная схема, для

которой эта функция является функцией проводимости. Эта схема содержит

наименьшее число ребер.

Чтобы построить минимальную КС, надо выписать минимальную ДНФ для данной

функции, упростить путем вынесения за скобки, нарисовать П-сеть,

реализующую КС для функции и постараться найти мостиковые соединения.

Минимальные пути в графах

Путем в графе (в орграфе) называется маршрут, движение по которому любого

ребра проходит в соответствии с направлением этого ребра.

Контуром в орграфе называется замкнутый путь, в котором вершины не

повторяются (кроме первой и последней).

Орграф, в котором нет ни одного контура, называется бесконтурным.

Первая задача о минимальном пути.

Дан граф. Выделено две вершины. Найти путь из одной вершины в другую,

состоящий из наименьшего числа ребер.

Введем обозначения

Г(V) – множество вершин, в которые можно попасть из вершины V, пройдя

только по одному ребру в его направлении.

Г-1(V) – множество вершин, из которых можно попасть в вершину V, пройдя

только по одному ребру.

Алгоритм.

1. Исходной вершине A присваиваем метку 0.

2. Любому Г(А), которые еще не имели меток, присваиваем метку М = 1.

3. Для любой V, принадлежащей Г(А) находим Г(V) и любой V, принадлежащему

Г(V), если она не имела метку, даем метку 2.

4. И так далее до тех пор, пока конечная вершина не получит метку.

5. Выбираем путь по Г-1(V).

Может произойти такое, что пути из А в В нет вообще.

Тогда на некотором шаге при обратном ходе нужной вершины нет.

Вторая задача.

Если каждому ребру поставить в соответствие некоторое целое положительное

число, называемое его длиной и требуется найти путь из А в В, такой, что

[pic]i = minimum. (r или l – длина ребра)

Алгоритм будет следующий.

1. Метка для ребра А ?1 ’ 0

Для Vi ?i = +(бесконечность) – очень большое число, большее суммы всех длин

ребер всего графа.

L(Vi, Vj) – длина ребра, идущего из вершины Vi в Vj. Направление важно.

2. Для любого ребра из графа проверяем выполнение неравенства.

?j - ?i > L(Vi, Vj) *

Если это неравенство выполняется, то меняем метку ?j на новую.

?j = ?i + L(Vi, Vj) и так до тех пор, пока выполняется *.

Если * нигде не выполняется, то та метка, которая будет стоять у вершины В

и будет равна длине минимального пути из А в В, а сам путь строится

движением назад из В в А.

Г-1(В) Существует такое ребро Vi1, для которого выполнено равенство.

?b - ?i1 = L(Vi1,B)

Затем Г-1(V1) Существует V2, где ?(V1) - ?(V2) = L(V1, V2) и т.д. пока не

вернемся в вершину А.

Путь минимальной длины найден.

Остов графа минимальной длины.

Остов – дерево, содержащее все вершины графа и какие-то из его ребер.

Если каждому ребру графа поставлена в соответствие его длина, то требуется

найти такой остов, сумма длин ребер которого минимальна.

Алгоритм

1. Перенумеруем все ребра графа в порядке возрастания их длин.

2. Просматриваем ребра, начиная с первого. Если x1 не является петлей, мы

его включаем в остов и переходим к следующему ребру. Если оно не является

петлей и не образует с уже имеющимися ребрами цикла, мы его включаем в

остов. И так до тех пор, пока не рассмотрим все ребра.

Остов минимальной длины найден.

Лекция 14

Парное сочетание (паросочетание) двудольных графов

Двудольным графом называется граф, у которого множество вершин можно

разбить на два непересекающихся подмножества так, что ребра соединяют

вершины из разных подмножеств.

Паросочетанием в двудольном графе называется любое множество попарно

несмежных ребер (у них нет общих вершин).

Паросочетание называется максимальным для данного графа, если оно содержит

наибольшее число ребер для всех возможных паросочетаний.

Паросочетание называется совершенным (из множества v в множество w), если

число ребер в нем совпадает с числом вершин в подмножестве c.

Для любого подмножества S через ф(S) обозначим те вершины из множества w,

которые соединяются ребрами с вершинами подмножества S.

Теорема Холла (без доказательства)

Для того, чтобы в двудольном графе существовало совершенное паросочетание,

необходимо и достаточно, чтобы для любого подмножества S из множества V

выполнялось условие [S] <= [ф(S)].

Венгерский алгоритм нахождения максимального паросочетания.

Дан двудольный граф. Все определения для графа справедливы.

Полным паросочетанием называется паросочетание (ПС), к которому нельзя

добавить ни одного ребра графа, не нарушив условие несмежности ребер.

1. Перебираем все ребра в любом порядке. Все несмежные ребра включаем в

паросочетание.

Ребра, входящие в полное паросочетание, будем называть толстыми. Остальные

ребра считаем тонкими.

Вершины, которые соединены толстыми ребрами – насыщенные. Остальные –

ненасыщенные.

Чередующейся цепью называется цепь, в которой тонкие и толстые ребра

чередуются.

Тонкой чередующейся цепью называется чередующаяся цепь, соединяющая 2

ненасыщенные вершины (В ней тонких ребер на 1 больше, чем толстых).

1. Находим полное паросочетание.

2. Для этого паросочетания ищем тонкую цепь. Если ее нет, то данное

паросочетание максимально и алгоритм закончен.

3. Если же она существует, то проводим перекраску ребер.

4. Толстые ребра тонкой цепи делаем тонкими, а тонкие – толстыми.

5. Получаем новое паросочетание, т.е. из исходного паросочетания удаляем те

толстые ребра, которые входили в тонкую цепь и вместо них добавляем

тонкие ребра из этой цепи.

6. Переходим на шаг 2.

Количество ребер в новом паросочетании увеличится на 1.

Максимальное паросочетание (МПС) найдено.

Совершенное ПС – МПС обязательно.

Матрицы смежности двудольных графов.

A(M,N)

[V] = M

[W] = N

Aij = 1, если есть ребро ViWj

Если его нет, то Aij = 0.

[pic]

Чтобы найти полное паросочетание, нужно найти единицы, которые находятся в

разных строках и разных столбцах.

Алгоритм – тот же самый.

При поисках мы можем двигаться по строкам и на углы в 90 градусов.

Алгоритм оптимального назначения

Есть m работников и m работ.

Каждый из работников выполняет каждую работу с определенной эффективностью.

Требуется распределить работы таким образом, чтобы каждый работник выполнял

только одну работу, выполнялись все работы и суммарная эффективность была

максимальна среди всех возможных таких распределений.

A = (aij) – матрица эффективности.

А(М*М)

А = [pic]

В терминах матрицы эффективности задача состоит в нахождении М элементов,

расположенных в разных строках и разных столбцах, чтобы их сумма была

максимальной.

Дан двудольный полный граф с V = M, W = M

Даны длины ребер.

Задача состоит в нахождении совершенного паросочетания, сумма длин всех

ребер которого максимальна.

Алгоритм.

| |0 |0 |0 |0 |

|4 |1 |2 |3 |4 |

|4 |1 |4 |4 |2 |

|6 |2 |5 |6 |3 |

|6 |1 |6 |4 |4 |

1. Всем вершинам Vi даем метку аi = max по всем элементам нужной строки.

По всем j присваиваем метку 0.

2. Ищем ребра, для которых выполняется условие

Ai + Bj = Aij

Строим граф, в который входит все вершины исходного графа и найденные

ребра.

3. В построенном графе ищем максимальное паросочетание. Если найденное

паросочетание совершенно, то алгоритм закончен. Если нет, то переходим

дальше.

4. Из теоремы Холла существует подмножество S из V, [S] > ф(S).

Ищем это подмножество.

Для каждой вершины Vi из S метку Ai уменьшают на 1, а для wj из ф(s) метку

Vj увеличивают на 1.

5. Переходим на начало шага 2 с новыми значениями меток.

Лекция 15

Потоки в транспортных сетях

Введем обозначения

V – вершина орграфа

M-(V) – множество ребер, для которых вершина V является концом.

M+(V) – множество ребер, для которых вершина V является началом.

Транспортной сетью называется связный орграф без петель, для которого

выполнены следующие условия

1. Существует только одна вершина A, для которой M-(А) – пустое множество.

А – исток.

2. Имеется только одна вершина B, для которой M+(B) – пустое множество. В –

сток.

3. Каждому ребру графа поставлено в соответствие целое неотрицательное

число, называемое пропускной способностью данного ребра.

2(1) 3(1)

1(1)

6(0)

5(5)

1(1) 4(1)

2(1)

Потоком в транспортной сети (ТС) называется целочисленная функция,

определенная на любых ребрах ТС и удовлетворяющая следующим свойствам

1. ф(X) <= C(X), где С(X) – пропускная способность ребра.

На всех ребрах значение функции потока не превосходит значения пропускной

способности ребра. Значение функции потока ставим рядом со значением

пропускной способности ребра в скобках.

2. Для каждой внутренней вершины V транспортной сети, не равной A или B

выполняется следующее условие: суммарная функция потока по ребрам, входящим

в вершину, равна суммарной функции потока по ребрам, исходящим из вершины

(сколько втекает, столько и вытекает).

Величиной потока [ф] = val(ф) называется число, равное сумме функций потока

по всем ребрам, выходящим из вершины А или сумма всех функций потока по

всем ребрам, входящим в вершину В.

Выбор потока.

1. Берем путь из А в В.

2. Выбираем минимальную пропускную способность и ставим ее в соответствие

каждому ребру из пути.

3. Просматриваем все остальные ребра. Если они не пересекаются, то

проделываем для них то же самое, начиная с п1. Всем остальным ребрам

ставим в соответствие значение функции потока, равное 0.

Поток в транспортной сети называется максимальным, если выполнено условие

Val(ф) ? Val(Ф*)

Ф* = maximum

Любое подмножество S транспортных вершин, содержащих исток и не содержащих

сток, определяет разрез, отделяющий исток от стока (разрез).

Разрез состоит из всех вершит тех ребер, которые имеют свои начала в

вершинах множества S, а концы – из дополнения к множеству S.

Пропускной способностью разреза K называется сумма значений пропускных

способностей всех ребер этого разреза.

Разрез K** называется минимальным, если для любого другого разреза

выполнено условие C(K**) ? C(K).

Теорема Форда – Фалькерсона (без доказательства).

В транспортной сети величина максимального потока равна пропускной

способности минимального разреза.

Алгоритм нахождения максимального потока (Алгоритм Форда – Фалькерсона).

1. Берем любой поток в транспортной сети.

2. Строим граф перестроек g* по следующему правилу:

В него входят все вершины исходного графа g.

Те ребра, на которых значение функции потока в исходном графе g были

равны 0, входят в новый граф без изменений со своими пропускными

способностями.

Все ребра, на которых ф(x) > 0 в новом графе g* заменяются двумя

ребрами x* и x**. Ребро x* направлено в ту же сторону, что и x, и

пропускная способность c(x*) = c(x) – ф(x).

Ребро x** направлено в противоположную сторону ребру x, и пропускная

способность c(x**) = ф(x).

Ребра с нулевой пропускной способностью можно не рисовать.

3. В графе g* ищем путь из А в В по ребрам с ненулевой пропускной

способностью. Если его нет, то имеющийся поток является максимальным и

алгоритм закончен. Иначе переходим к пункту 4.

(Этот путь называется увеличенной цепью. ? ’ min(c(x)) – минимальное

значение пропускной способности этой цепи).

4. Меняем значение функции потока в графе g для тех ребер, которые

соответствуют найденному пути в графе перестроек по следующему правилу:

Если направление ребра x в графе g совпадает с направлением пути, то новое

ф(x) = ф(x) + ?

Если же направление противоположно направлению пути, то ф(x) = ф(x) - ?

5. Переходим на шаг 2 с новым потоком.

Графы и бинарные отношения

Напомним, что бинарным отношением на множестве A называется любое подмножество R

множества

A , состоящего из всевозможных упорядоченных пар элементов множества A.

Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что

понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие

типы графов без кратных ребер – это частные виды бинарных отношений. Отношение R называется

рефлексивным, если для любого x∈ A пара (x, x) принадлежит R, и антирефлексивным, если ни

одна такая пара не принадлежит R. Оно называется симметричным, если для любых x, y ∈ A из

( ) x, y ∈ R следует ( ) y, . x ∈ R Обыкновенный граф – не что иное, как антирефлексивное

симметричное отношение.