Линейное регрессионное уравнение

Регрессионный анализ является одним из основных методов современной математической статистики. Однофакторный регрессионный анализ позволяет найти зависимость между двумя переменными.

Пусть мы имеем n наблюдений (x_i, y_i, i = 1,2,…n), где x_i - значения независимого (факторного) переменного (например, доходы населения), а y_i - значения зависимого (результативного) переменного (например, расходы). Графически эти данные задаются n точками в двумерной системе координат YOX (рис. 6.1).

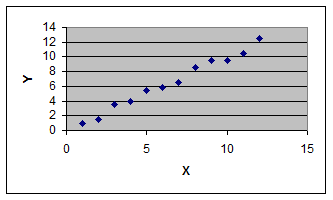
Рис.6.1. Наблюдения (x_i, y_i)

Нашей задачей является нахождение зависимости y от x по данным (x_i, y_i), т.е. «подгонка» этих точек какой-то функцией y = f(x).

Простейшая модель зависимости y = f(x) это линейная модель, когда y = a + bx, где a и b неизвестные параметры. Для этой модели задача регрессии решается до конца, а полученные результаты являются базовым для регрессии других, в частности, нелинейных моделей.

В этой модели переменная x детерминированная (без случайных ошибок) величина, а наблюдаемые y_i, как правило, отличаются от y = a + bx. Они случайные величины, поэтому выражение для y_i пишется в виде y_i = a + bx_i + e_i, где e_i - случайные ошибки (отклонения y_i от y). Причины возникновения случайных ошибок e_i различные: а) так называемый «человеческий фактор»; б) не учет всех факторов; в) неправильный выбор модели и т.д.

Это уравнение называется однофакторным линейным регрессионным уравнением.

Метод наименьших квадратов

Параметры a и b можно найти разными методами, но наилучшим методом является метод наименьших квадратов (МНК). Суть МНК заключается в том, что требуется, чтобы сумма квадратов случайных ошибок была минимальной, чтобы y = f(x) наиболее близко находилась бы к точкам (x_i, y_i):

.

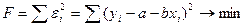Решения для a и b называются оценками и определяются через ковариацию x, y и дисперсию x:

, .

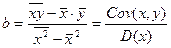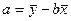Поставляя оценки a и b в линейное уравнение, находим регрессию ŷ = a + bx.

Утверждение, что a и b являются наилучшими оценками, а регрессия наилучшей «подгонкой», доказывается теоремой Гаусса-Маркова.

Теорема Гаусса-Маркова. В предположениях модели y_i = a + bx_i + e_i, x_i - детерминированная величина, M(e_i) = 0, D(e_i) = s², M(e_ie_j) = 0, i¹j, оценки a и b, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

@ Задача 1.По данным таблицы найти неизвестные параметры регрессионного уравнения y = a + bx:

x
y

Решение: n = 4; Σx = 10; Σy = 26; Σxy = 80; Σ x² = 30; 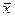= 2,5; 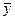= 6,5; 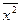= 7,5; 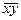= 20; D(x) = 7,5 – 6,25 = 1,25; b = (20 – 2,5·6,5)/(7,5 – 6,25) = 3; a =6,5 – 2,5·3 = – 1.

В итоге получаем: ŷ = – 1 + 3x.

Качество оценки: коэффициент детерминации

После построения уравнения регрессии возникает вопрос о качестве оценки.