Центральное растяжение (сжатие) прямого бруса. Определение деформаций и перемещений. Жёсткость бруса при растяжении (сжатии). Привести примеры соответствующих расчётов
Центральное напряжение (сж.) прямого бруса см. в вопросе 8.
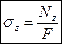 .
.
При центральном растяжении (сж.) бруса в поперечном направлении в сечении возникает только нормальное напряжение σz, постоянное во всех точках поперечного сечения и равное Nz/F. 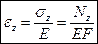 , где EF – жёсткость бруса при растяжении (сжатии). Чем больше жёсткость бруса, тем меньше деформируется бус при одной и той же силе. 1/(EF) – податливость бруса при растяжении (сжатии).
, где EF – жёсткость бруса при растяжении (сжатии). Чем больше жёсткость бруса, тем меньше деформируется бус при одной и той же силе. 1/(EF) – податливость бруса при растяжении (сжатии).
Центральное растяжение (сжатие) прямого бруса. Статически неопределимые системы. Раскрытие статической неопределимости. Влияние температурного и монтажного факторов. Привести примеры соответствующих расчётов.
Центральное напряжение (сж.) прямого бруса см. в вопросе 8.
Если число линейно-независимых уравнений статики меньше числа неизвестных, входящих в систему этих уравнений, то задача по определению этих неизвестных становится статически неопределимой. 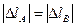 (На сколько удлинится одна часть, на столько сожмётся вторая).
(На сколько удлинится одна часть, на столько сожмётся вторая).
Нормальные условия - 20º С. 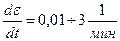 . f(σ,ε,tº,t)=0 – функциональная зависимость между 4 параметрами.
. f(σ,ε,tº,t)=0 – функциональная зависимость между 4 параметрами.
Опытное изучение механических свойств материалов при растяжении (сжатии). Принцип Сен-Венана. Диаграмма растяжения образца. Разгрузка и повторное нагружение. Наклёп. Основные механические, прочностные и деформационные характеристики материала.
Механические свойства материалов вычисляют с помощью испытательных машин, которые бывают рычажными и гидравлическими. В рычажной машине усилие создаётся при помощи груза, действующего на образец через систему рычагов, а в гидравлической – с помощью гидравлического давления.
Принцип Сен-Венана: Характер распределения напряжения в поперечных сечениях достаточно удалённых (практически на расстояния, равные характерному поперечному размеру стержня) от места приложения нагрузок, продольных сил не зависит от способа приложения этих сил, если они имеют один и тот же статический эквивалент. Однако в зоне приложения нагрузок закон распределения напряжения может заметно отличаться от закона распределения в достаточно удалённых сечениях.
Если испытуемый образец, не доводя до разрушения, разгрузить, то в процессе разгрузки зависимость между силой Р и удлинением Δl образец получит остаточное удлинение.
Если образец был нагружен на участке, на котором соблюдается закон Гука, а затем разгружен, то удлинение будет чисто упругим. При повторном нагружении пропадёт промежуточная разгрузка.
Наклёп (нагартовка) – явление повышения упругих свойств материала в результате предварительного пластического деформирования.
Предел пропорциональности – наибольшее напряжение, до которого материал следует закону Гука.
Предел упругости – наибольшее напряжение, до которого материал не получает остаточных деформаций.
Предел текучести – напряжение, при котором происходит рост деформации без заметного увеличения нагрузки.
Предел прочности – максимальное напряжение, которое может выдержать образец, не разрушаясь.
Физический и условный пределы текучести материалов при испытании образцов на растяжение, предел прочности. Допускаемые напряжения при расчёте на прочность центрально растянутого (сжатого) бруса. Нормативный и фактический коэффициенты запаса прочности. Привести числовые примеры.
В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация εост=0,002 или 0,2%. В некоторых случаях устанавливается предел εост=0,5%.
max|σz|=[σ]. 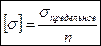 , n>1(!) – нормативный коэффициент запаса прочности.
, n>1(!) – нормативный коэффициент запаса прочности.
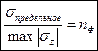 - фактический коэффициент запаса прочности. n>1(!).
- фактический коэффициент запаса прочности. n>1(!).
max|σz|растяж≤[σ]растяж; max|σz|сжатия≤[σ]сжатия.
