Доверительные интервалы математического ожидания и для дисперсии нормально распределенной случайной величины

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения известно. Требуется оценить неизвестное математическое ожидание a по выборочному среднему 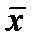. Найдем доверительные интервалы, покрывающие параметр a с надежностью .

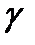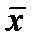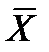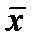Будем рассматривать выборочное среднее , как случайную величину (т.к. меняется от выборки к выборке), и выборочные значения 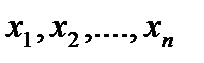, как одинаково распределенные независимые случайные величины 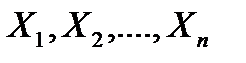(эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение – s. Так как случайная величина X распределена нормально, то и выборочное среднее 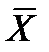также распределено нормально.

Выражение для искомого доверительного интервала вычисляется по формуле 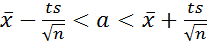с надежностью 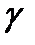. по табл Стьюдента находится с заданным объемом выборки и надежностью.

42. СТАТИС-АЯ ГИПОТЕЗА, СТАТИС-Й КРИТЕРИЙ, ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА.

Статистическойназывают гипотезу о виде неизвестного распределения или о параметрах известных распределений. Примеры статистических гипотез: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных распределений равны между собой.

Ошибка первого родасостоит в том, что будет отвергнута правильная гипотеза.Ошибка второго родасостоит в том, что будет принята неправильная гипотеза. Следует отметить, что последствия ошибок могут оказаться различными. Если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение «продолжать строительство» несмотря на опасность обвала дома, то эта ошибка второго рода может привести к многочисленным жертвам. Иногда, наоборот, ошибка первого рода влечет более тяжелые последствия.

Статистическим критерием(или просто критерием) называют случайную величину (обозначим ее через K), которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий .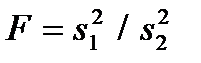

43. КРИТИЧЕСКАЯ ОБЛАСТЬ, МОЩНОСТЬ КРИТЕРИЯ.

Критической областьюназывают совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы(областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают.

Так как критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы. Такие точки называются критическими точками.

Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области.

Правостороннейназывают критическую область, определяемую неравенством 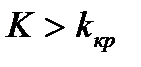, где 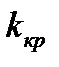– положительное число.

Левостороннейназывают критическую область, определяемую неравенством 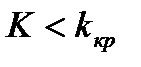, где 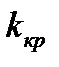– отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами 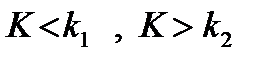, где .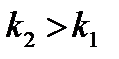

44. СХЕМА ПРОВЕРКИ СТАТ-ОЙ ГИПОТЕЗЫ.

1. Сформулировать нулевую H₀ и альтернативную Н₁, гипотезы.

2. Выбрать уровень значимости α.

3. В соответствии с видом выдвигаемой нулевой гипотезы Н₀

иыбрать статистический критерий для ее проверки, т. е. — специально подобранную случайную величину К, точное или приближенное распределение которой заранее известно.

4. По таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти крити­ческое значение К_кр (критйческую точку или точки).

5. На основании выборочных данных по специальному алгоритму вычислить наблюдаемое значение критерия К_набл

6. По виду конкурирующей гипотезы Н₁ определить тип критической области.

7. Определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия К_на6п, и в зависи­мости от этого -— принять решение относительно нулевой гипотезы Н₀.

Можно принять решение относительно нулевой гипотезы Н₀ путем сравнения наблюдаемого и критического значения критерия.