Методы исследования термодинамических процессов. энтропия газов

При исследовании все процессы рассматриваются как равно­весные и обратимые.

Прежде чем рассматривать порядок исследования термо­динамических процессов, введем пятый параметр состояния газа - энтропию S. Энтропия характеризует направления протекания теплообмена между системой и внешней средой.

Для произвольной массы газа G (кг) энтропию S измеряют в кДж/K, а энтропию 1 кг газа обозначают буквой s и измеряют в кДж/(кг • К), т.е. в тех же единицах, что и массовую теплоемкость.

В термодинамике определяют лишь изменение энтропии ΔS =S 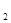– S . В связи с этим условно считают, что при 0 °C и при любом давлении энтропия S, так же как и внутренняя энергия и, равна нулю.

Не прибегая к помощи высшей математики, для произ­вольного (политропного) термодинамического процесса можно записать:

где ΔQ - количество теплоты, участвующей в произвольном элементарном термодинамическом процессе, кДж/кг;

ΔS - изменение энтропии в данном элементарном процессе, кДж/(кг∙К).

Отношение Δq/T называется приведенной теплотой и представляет собой качественную характеристику процесса преобразования теплоты.

Изменение энтропии как функции состояния зависит не от пути протекания процесса (т.е. пути перехода рабочего тела), а от начального и конечного состояния,

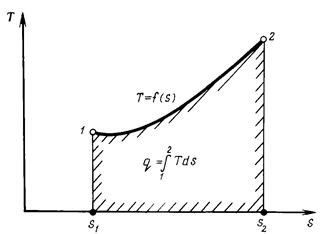
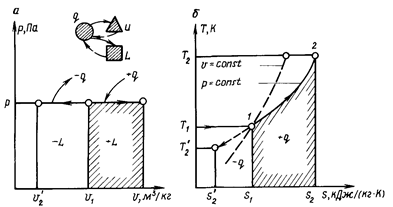
Введение понятия энтропии как параметра состояния рабо­чего тела позволяет применить для исследования термодинами­ческих процессов новую (pv-диаграмма введена ранее) прямо­угольную систему координат Т, s, в которой по оси абсцисс в соответствующем масштабе откладывают энтропию s, а по оси ординат - абсолютную температуру Т. Такая диаграмма назы­вается Ts-диаграммой (рис. 1.6).

В этой диаграмме площадь, ограниченная перпендикуля­рами, опущенными на ось абсцисс из точек начального и конечного состояний, и осью абсцисс, выражает количество сообщенной или отнятой теплоты q. Поэтому Ts-диаграмму называют также тепловой или энтропийной. Так как в уравнении (1.54) температура T - величина всегда положи­тельная, то Δs и Δq имеют одинаковые знаки, т.е. если теплота q подводится к газу (величина положительная), то и ΔS возрастает. И наоборот, если ΔQ отводится (величина отрицательная), то и ΔS уменьшается. Это одно из наиболее важных свойств энтропии.

При исследовании термодинамических процессов опреде­ляют:

1) уравнение процесса и его графическое изображение в системе координат p, v,

2) связь между основными параметрами состояния газа;

3) изменение внутренней энергии газа Δu и величину работы расширения l;

4) количество теплоты q, сообщаемой газу или отводимой от него;

5) графическое изображение процесса в системе координат T, s.

ИЗОХОРНЫЙ ПРОЦЕСС

Процесс, протекающий при постоянном объеме, называется изохорным. Изохорный процесс применяется, в частности, при расчетах теоретических циклов карбюраторных двига­телей внутреннего сгорания (ДВС). Уравнение процесса

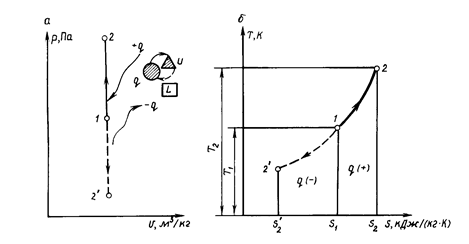
В pv-анаграмме (рис. 1.7) графиком процесса является прямая линия, перпендикулярная оси абсцисс и называемая изохорой.

При неизменном объеме Δυ = 0 площадь, соответствующая в ρυ-диаграмме работе расширения l, также равна нулю. Следовательно, в изохорном процессе работа расширения газа l = 0.

Зависимость между изменяющимися параметрами газа определяется из уравнения (1.13), записанного для начального l и конечного 2 (см. рис. 1.7, а) состояний:

Разделив почленно, получим

Уравнение (1.56) показывает, что в изохорном процессе давление газа прямо пропорционально абсолютной темпера­туре.

Поскольку в данном процессе l = 0, то согласно формуле (1.48) подводимая к рабочему телу теплота q полностью расходуется на изменение внутренней энергии:

q = и, - и, = ^u =с„(Г, - Т.). (1.58)

В процессе 1-2' (см. рис. 1.7, а) теплота q отводится от газа, в результате чего снижается его температура. Следо­вательно, процесс 1 - 2' - охлаждение рабочего тела (- q).

Изменение удельной энтропии ΔS = S – S , в изохорном процессе (при постоянной теплоемкости C 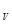) подсчитывают по формуле

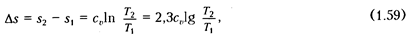
где ΔS - изменение энтропии газа, кДж/(кг • К); C 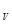- средняя массовая теплоемкость газа в процессе при v = idem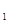; T , T ; -температура соответственно в начале и конце процесса, К.

Уравнение (1.59) показывает, что изохорный процесс изображается в координатах Т, s логарифмической кривой (см. рис. 1.7, б) и протекает так, что при подводе теплоты (+ q) увеличиваются энтропия и температура газа, а при отводе теплоты (- q) эта параметры уменьшаются.

ИЗОБАРНЫЙ ПРОЦЕСС

Процесс, протекающий при постоянном давлении, называется изобарным. Такой термодинамический процесс может про­текать в цилиндре, поршень которого перемещается без трения, так что давление в цилиндре постоянно и равно давлению на поршень окружающей среды.

В pv-диаграмме (рис. 1.8) изобара изображается прямой линией, параллельной оси абсцисс (оси удельных объемов v):

1 - 2 - с подводом теплоты (+ q) и 1 - 2' - с отводом теплоты

(-q).

Уравнение процесса

Зависимость между переменными значениями основных

параметров состояния рабочего тела определяют из уравнения Клапейрона (1.13), записанного для точек 1 и 2:

откуда получают

Таким образом, при увеличении удельного объема газа в изобарном процессе температура его повышается, при умень­шении - понижается.

Работа расширения газа l (см. рис. 1.8, а) изображается площадью под линией процесса 1 - 2 - расширение (+ l) и под линией 1 - 2' - сжатие (- l). Из рис. 1.8, а видно, что работу расширения можно определить по уравнению

Если количество газа обозначить G (кг), то формула для вычисления работы расширения L принимает вид

L =p(V,- V.) = GR(T,-T,). (1.64)

Приняв в формуле (1.63) разность абсолютных температур T – Т = 1 К, получим, что l = R. Это позволяет определить физический смысл газовой постоянной как удельной работы расширения 1 кг идеального газа при нагревании на 1 К при p = idem.

Изменение внутренней энергии идеального газа при извест­ных значениях температур в начале (Т 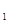) и конце (T 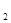) процес­са (считая теплоемкость C 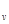постоянной) выражается уравне­нием

Количество теплоты, сообщенной рабочему телу в данном процессе, определяется из математического выражения первого закона термодинамически (1.48) с учетом формул (1.63) и (1.65):

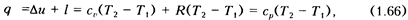
так как согласно формуле (1.30) С 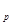= 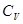+ R.

Изменение удельной энтропии в изобарном процессе под­считывается по уравнению

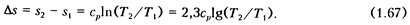
Следовательно, в Ts-диаграмме изобарный процесс, так же как и изохорный, изображается логарифмической кривой, но более пологой по сравнению с изохорой (см. рис. 1.8, б). Такое относительное расположение изобары и изохоры в Ts-диаграмме обусловлено тем, что удельная теплоемкость С > .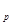

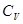Количество теплоты процесса q графически изображает­ся площадью (см. рис. 1.8, б), ограниченной кривой процесса (1 - 2, 1 - 2' ) и осью абсцисс.

ЭНТАЛЬПИЯ ГАЗА

В процессах, связанных с расчетом котельных установок, паровых турбин, а также с сушкой и охлаждением сельско­хозяйственной продукции, используют параметр состояния рабочего тела (газа), называемый энтальпией - теплосодержа­нием. Удельная энтальпия обозначается h и измеряется в кДж/кг. Введение понятия "энтальпия" дополнительно к ранее рассмотренным (давление, удельный объем, темпера­тура, внутренняя энергия, энтропия) р, v, Т, и, s облегчает исследование процессов в тепловых двигателях, особенно в паровых турбинах.

Этот параметр состояния равен

Если в (1.68) подставить вместо и и pv их значения, а именно и = c 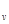Т и pv = RT, получим

Следовательно, энтальпия идеального газа численно равна произведению массовой теплоемкости при постоянном дав­лении на абсолютную температуру. Понятию "энтальпия" можно дать следующее пояснение. Пусть в цилиндре под поршнем находится 1 кг газа. На поршень сверху положен груз массой G, уравновешивающий давление газа р.

Очевидно,

где F - площадь поршня.

Вся система находится в равновесии. В этом случае энергия системы (1 кг газа и груз) будет равна внутренней энергии газа и и потенциальной энергии груза массой G, поднятого на высоту H, равную высоте цилиндра:

Так как FH = и (т.е. объему 1 кг газа в цилиндре), то полная энергия системы равна и + pv = h - величине энтальпии газа.

В теплотехнических расчетах обычно требуется знать изменение энтальпии

(Δh 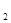= h – h 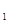), а не ее абсолютное значение. Поэтому начало отсчета

(0 К или 0 °С) для конечного результата (Δh) значения не имеет.

Используя формулу (1.48), нетрудно доказать, что для любого газа в процессе при постоянном давлении (изобарном, р = idem) подводимая теплота равна разности энтальпии в конце и начале процесса:

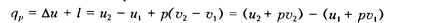
или с учетом (1.68)

Следовательно, в изобарном процессе количество подведен­ной теплоты 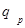определяется разностью энтальпии в конце (h 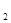) и начале (h 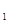) процесса.