Теоретические основы решения транспортной задачи

Матрицей перевозок называется матрица X=(x_ij)_m´n с планом перевозок, при котором достигается минимум целевой функции.

8.2.1. Теорема. Транспортная задача (8.1) разрешим тогда и только тогда, когда суммарные запасы и суммарные потребности совпадают: = .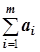

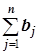Если суммарные запасы и суммарные потребности совпадают ( 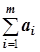= 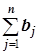), то задача называется задачей закрытого типа. В противном случае задача называется задачей открытого типа. В задаче открытого типа требуется составить такой план перевозок, при котором запасы поставщиков будут использованы по максимуму, потребности потребителей будут удовлетворены также по максимуму (и, конечно, суммарные перевозки будут минимальными).

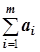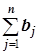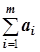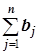Забегая вперёд отметим, что задача открытого типа решается сведением её к задаче закрытого типа введением фиктивных либо потребителя П_n+1 с потребностью b_n+1= - (при > ), либо поставщика P_m+1 с запасом a_m+1= 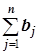- 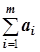(при 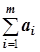< 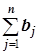). При этом стоимости c перевозок с фиктивными участниками делается произвольным постоянным числом, например, c=0. Далее задача решается обычным образом. Только ответ формулируется с реальными перевозками (без учёта фиктивных перевозок).

Так что везде ниже предполагается, что мы имеем дело с задачей закрытого типа.

8.2.2. Теорема. Ранг матрицы системы ограничений транспортной задачи (8.1) равен m+n-1.

Это означает, что любой опорный план задачи содержит, вообще говоря, m+n-1 ненулевых компонент. Напоминаем, что эти компоненты соответствуют базисным переменным, и если хотя бы одна из них равна 0, то опорное решение называется вырожденным. Компоненты, соответствующие свободным переменным, равны нулю.

Так же, как и в симплекс-методе, решение транспортной задачи сопровождается заполнением очередной таблицы. По сути это - та же транспортная таблица, только в клетки таблицы заносятся значения компонент x_ij очередного опорного плана, соответствующие базисным переменным (x_ij). Таким образом, на каждом шаге в транспортной таблице должна быть заполнено m+n-1 клеток.

Пример 2. В Таблице 8.2 отражён опорный план задачи Таблицы 8.1:

			Таблица 8.2
bj ai

Такую таблицу будем называть заполненной. Вписанные значения x_ij будем называть содержимыми клеток.

При этом плане имеем x₁₁=70, x₁₂=20, x₂₂=10, x₂₃=20, x₃₃=0, x₃₄=40. Как видим, заполнено m+n-1=3+4-1=6 клеток таблицы. Так как x₃₃=0, то план вырожден.

Помеченным циклом называется замкнутая ломаная, одна вершина которой находится в пустой клетке, а остальные - в некоторых из заполненных клеток, любые два смежных звена ломаной «ломается» под углом 90^о (перпендикулярны друг другу) и вершины любого звена находятся либо в одном и том же столбце, либо в одной и той же строке. При этом вершины цикла (клетки с вершинами цикла) помечены знаками «+» и «-» с чередованием, начиная с «+» в пустой клетке.

8.2.3. Теорема. Для любой пустой клетки заполненной транспортной таблицы существует помеченный цикл, и он единствен.

Пример 3. Ниже в таблицах 8.3 и 8.4 приведены помеченные циклы. Один «берёт начало» в клетке (2, 1) (Таблица 8.3), а другой - в клетке (1, 4) (таблица 8.4).

			Таблица 8.3
bj ai
	70 -	+
	+	-

			Таблица 8.4
bj ai
		20 -		+
		+	-
			+	-

Сдвигом по циклу называется следующая манипуляция с транспортной таблицей с помеченным циклом: из содержимого клеток со знаком «-» выбирается минимальное содержимое m= 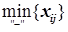, это число m вычитается из содержимых всех клеток со знаком «-» и прибавляется к содержимому клеток со знаком «+». При этом если клетка со знаком «-» и содержимым m= 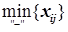единственна, то эта клетка становится пустой. Если клеток со знаком «-» и содержимым m= 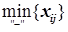несколько, то одну из них оставляем пустой, а в остальных записываем 0.

Пример 3. После сдвига по циклу в Таблице 8.3 получаем таблицу 8.5:

			Таблица 8.5
bj ai

А после сдвига по циклу в Таблице 8.4 получаем Таблицу 8.6:

			Таблица 8.3
bj ai

В таблице 8.4 имеем x₁₂=x₂₃=20, m= 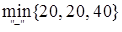=20 достигается в клетках (1, 2) и (2, 3). В таблице 8.6 клетку (1, 2) мы сделали пустой, а клетку (2, 3) заполнили нулём. Можно было поступить по другому: клетку (1, 2) заполнить нулём, а клетку (2, 3) сделать пустой.

8.2.4. Теорема. В результате сдвига по циклу получается новый опорный план.

8.2.5. Теорема. Если числа u_i (i=1, 2, …, m) и v_j (j=1, 2, …, n) - такие, что

u_i+v_j=c_ij (8.2)

для всех заполненных клеток, и

u_i+v_j£c_ij (8.3)

для всех пустых, то данный опорный план является оптимальным.

Величина D_ij=u_i+v_j-c_ij называется оценкой клетки (i, j). Таким образом, если для всех клеток имеем D_ij£0, то план оптимален.

8.2.6. Теорема. Если D_ij>D_kl, то при сдвиге по циклу в клетку (i, j) значение целевой функции уменьшится на величину, большую, чем при сдвиге по циклу в клетку (k, l).

Ясно, что равенства (8.2) являются «частью» нестрогих неравенств (8.3). Поэтому неравенства (8.3) будем называть критерием оптимальности опорного плана, хотя это по сути только достаточное условие оптимальности. Может оказаться, что условие (8.3) не выполняется для некоторой клетки, но тем не менее план является оптимальным. Но это - явление достаточно редкое. То есть если условие (8.3) не выполнено, то, скорее всего, план не оптимален, и переходят к другому опорному плану.