Классификация и условия оптимальности математических моделей задач оптимального проектирования

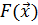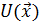Как было показано ранее, задачи параметрической оптимизации можно свести к математической модели минимизации функции n переменных, обозначенной нами или , в некоторой области изменения этих переменных D, определенной ограничениями-неравенствами вида 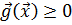(19), (21). В свою очередь, модели минимизации можно классифицировать по различным признакам: наличию или отсутствию ограничений, числу варьируемых параметров, виду целевых функций и ограничений.

Однако, прежде всего, следует определить, что мы понимаем под минимумом функции.

2.1 Глобальный и локальные минимумы. Рассмотрим вначале случай, когда ограничения на варьируемые параметры 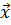отсутствуют: 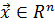. Тогда, в общем случае, минимизируемая функция 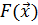может иметь в 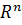несколько локальных минимумов 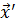. Тот из них, значение целевой функции в котором будет наименьшим, является глобальным минимумом.

Точка 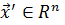является локальным минимумом функции 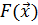в 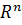, если существует такое число r>0, что для всех точек 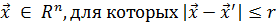, выполняется условие .

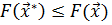Глобальным минимумом функции n переменных 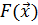в 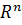называется такая точка 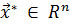, что для всех точек 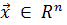выполняется условие .

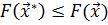Примеры локальных и глобальных минимумов функций одной и двух переменных показаны на рис. 2.1 и 2.2 соответственно.

Рассмотрим теперь задачу с ограничениями: 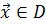, 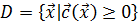(здесь, как и ранее, 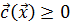означает, что каждая компонента вектора 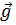должна быть неотрицательна: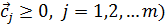

Точка 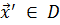является локальным минимумом функции 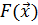в некоторой области 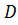, если существует такое число r>0, что для всех точек 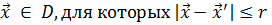выполняется .

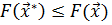Глобальным минимумом функции n переменных 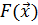в некоторой области 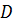называется такая точка 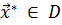, что для любых точек .

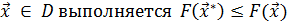На рис. 2.3 видно, как функция одной переменной, которая при отсутствии ограничений вообще не имела минимумов, при наличии ограничений имеет два локальных минимума, один из которых является глобальным. Рис. 2.4 показывает как функция двух переменных, имевшая при отсутствии ограничений один минимум (локальный и глобальный одновременно), при наличии ограничений, исключающих этот минимум, получает два новых локальных минимума.

2.2 Классификация математических моделей. Математические модели задач оптимального проектирования можно классифицировать по нескольким признакам.

1) По наличию или отсутствию ограничений на варьируемые параметры:

· Задачи минимизации функций, в которых ограничения на варьируемые параметры отсутствуют, называются задачами безусловной минимизации.

· Задачи минимизации функций, в которых присутствуют ограничения на варьируемые параметры, называются задачами условной минимизации.

2) По числу варьируемых параметров:

· Задачи минимизации функций одной переменной называются задачами одномерной минимизации.

· Задачи минимизации функций нескольких переменных называются задачами многомерной минимизации.

3) По числу точек локального минимума в области допустимых значений варьируемых параметров:

· При наличии одного локального минимума (одновременно являющегося глобальным), задача минимизации называется одноэкстремальной.

· При наличии нескольких локальных минимумов, задача минимизации называется многоэкстремальной.

4) В зависимости от вида минимизируемой функции и ограничений на варьируемые параметры:

· Если минимизируемая функция и ограничения являются линейными функциями, такая задача называется задачей линейного программирования. Обобщением задачи линейного программирования является задача сепарабельного программирования, в которой целевая функция и ограничения представляют собой суммы n функций, каждая из которых зависит только от одного варьируемого параметра.

· Если минимизируемая функция является квадратичной, а ограничения являются линейными функциями, такая задача называется задачей квадратичного программирования. Обобщением задачи квадратичного программирования является задача геометрического программирования, когда целевая функция и ограничения являются положительными полиномами.

· Если минимизируемая функция и ограничения являются нелинейными функциями, задача называется задачей нелинейного программирования. Если при этом целевая функция и область допустимых значений варьируемых параметров являются выпуклыми функциями, такую задачу называют задачей выпуклого программирования.

5) В зависимости от того, какие значения могут принимать варьирумые параметры:

· Если варьируемые параметры могут принимать только дискретные значения, получаем задачу дискретной оптимизации. В частном случае, когда варьируемые параметры могут иметь только целочисленные значения, задачу называют задачей целочисленного программирования.

Для решения задач линейного программирования применяются хорошо разработанные и строго обоснованные методы, такие как симплекс-метод [1]. В большинстве случаев задачи квадратичного и геометрического программирования также удается решить специальными методами [2] или свести к задачам линейного программирования. Так как названные задачи представляют ограниченный интерес для исследований в области естественных наук и инженерной практики, ограничимся в данном курсе ссылкой на литературные источники.

Задачи дискретного или целочисленного программирования зачастую оказываются более трудоемкими, чем задачи минимизации функций непрерывных (вещественных) переменных. Для решения таких задач используется метод ветвей и границ [1], а также появившиеся сравнительно недавно эволюционные алгоритмы [3]. Изложение этих методов также выходит за рамки настоящего курса.

Таким образом, далее мы будем рассматривать задачи нелинейного программирования: при отсутствии и наличии ограничений, одномерные и многомерные.

Большинство методов, которые мы будем рассматривать, строго обоснованы лишь для одноэкстремальных задач выпуклого программирования. Тем не менее, с некоторыми оговорками, большинство из них применимо и для решения невыпуклых задач. Что касается многоэкстремальных задач, то конструктивных методов, позволяющих гарантированно найти глобальный минимум функции, не существует. На практике с помощью рассматриваемых ниже методов решения одноэкстремальных задач пытаются найти все локальные минимумы в области допустимых значений варьируемых параметров.

Для различных классов моделей задач оптимального проектирования существуют различные методы решения. Тем не менее, можно выделить два подхода к построению этих методов. Первый основан на непосредственном применении условий оптимальности для соответствующего класса задач. Второй подход основан на применении эмпирических алгоритмов поиска оптимальных решений.

В зависимости от того, требуется для реализации того или иного метода решения задачи оптимального проектирования вычисление производных или нет, эти методы разделяют на следующие группы. Методы прямого поиска или методы нулевого порядка – методы, не требующие вычисления производных целевой функции. Градиентные методы – методы, требующие вычисления производных. Порядок градиентных методов определяется порядком старшей производной, которую необходимо вычислить. Обычно на практике используются градиентные методы первого, реже второго порядка. Градиентные методы обычно отличаются более высокой скоростью сходимости, чем методы прямого поиска. Однако, применение градиентных методов может оказаться затруднительным, если производные целевой функции приходится находить численно, и просто невозможным, если целевая функция не дифференцируема требуемое число раз.

2.3 Условия оптимальности.Перейдем к рассмотрению условий оптимальности математических моделей задач нелинейного программирования и попытаемся оценить возможности построения на основе этих условий конструктивных методов минимизации.

1) Безусловная минимизация унимодальной (имеющей один экстремум) функции одной переменной:

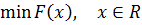(2.1)

Решение задачи (2.1) – локальный минимум функции одной переменной 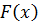– достигается в точке 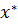, в которой

Таким образом, найти локальный минимум выпуклой унимодальной функции 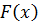можно, решив нелинейное уравнение 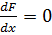. Для такой функции этот локальный минимум будет и глобальным. Для невыпуклой многоэкстремальной функции можно попытаться найти все локальные минимумы (все точки, в которых выполняется условие (2.2.)) и выбрать из них глобальный. На основе данного условия оптимальности разработан ряд конструктивных методов, наиболее популярным из которых является рассматриваемый ниже метод Ньютона.

2) Безусловная минимизация унимодальной (имеющей один экстремум) функции многих переменной:

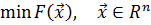(2.3)

Локальный минимум функции n переменных 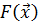достигается в точке 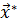, в которой

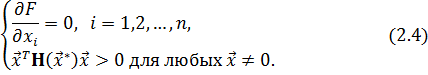
Здесь H – матрица Гессе - квадратная матрица размера 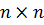с элементами
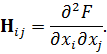Метод Ньютона-Рафсона основан на численном решении уравнения 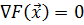и является прямым обобщением метода Ньютона для случая функции n переменных. Однако, метод Ньютона-Рафсона требует значительных затрат для вычисления вторых производных целевой функции и обращения на каждом шаге матрицы Гессе.

3) Условная минимизация унимодальной функции n переменных:

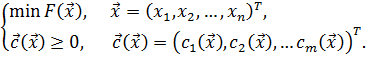(2.5)

Можно доказать [4], что необходимые условия минимума выпуклой функции 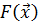при наличии ограничений вида 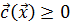, определяющих выпуклую область допустимых значений D, имеют следующий вид:

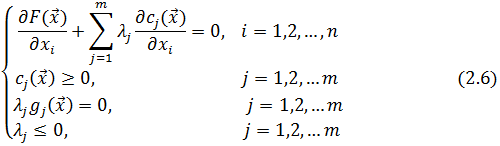
Условия (2.6) известны как условия Куна-Таккера. Из них можно найти значения компонент вектора 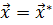, в которых достигается решение задачи (2.5), а также соответствующие значения множителей .

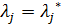Значение каждого из множителей 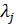, являющееся решением (2.6), равно взятой с противоположным знаком скорости изменения значения целевой функции 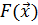в оптимальной точке 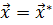при бесконечно малом изменении нулевой правой части неравенства :

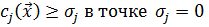Если правую часть неравенства 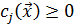увеличить на достаточно малую величину, то область допустимых значений уменьшится. При этом значение целевой функции в оптимальной точке может либо остаться неизменным (если оно лежит не на границе области допустимых значений, определяемой соответствующим неравенством), либо увеличиться. Таким образом, скорость изменения целевой функции при изменении правой части неравенства 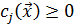положительна, а противоположная ей по знаку величина 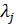в оптимальной точке должна быть отрицательна. Этот факт и выражает четвертое соотношение в (2.6).

Из третьего соотношения в (2.6) видно, что 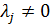только в том случае, если решение находится на границе области допустимых значений, определяемой соответствующим ограничением, то есть если 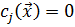. Если же 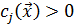, то решение находится на некотором расстоянии от границы области допустимых значений, определяемой этим ограничением. В этом случае достаточно малое изменение этого ограничения не повлияет на решение. Поэтому соответствующее .

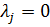Второе соотношение в условиях Куна-Таккера совпадает с ограничениями исходной задачи (2.5).

Для того, чтобы понять, как работают условия Куна-Таккера полезно самостоятельно с их помощью решить две простые задачи:

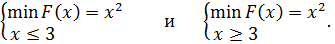
К сожалению, нахождение оптимального решения путем решения системы (2.6) не проще, чем решение исходной модели (2.5). Поэтому конструктивных численных методов минимизации, основанных на условиях Куна-Таккера нет.