Закон распределения Пуассона, его определение, свойства и примеры

Определение. Будем говорить, что случайная величина εраспределена по закону Пуассона с параметром λ, еслиона принимает значения из множества { 0,1,…,n, …} с вероятностями P { ε=m} = (λ^m/m!)*e^{- λ}.

Теорема. Если случайная величина εраспределена по закону Пуассона с параметром λ, то и математическое ожидание, и дисперсия этой случайной величины равны параметру λ.

Свойства распределения Пуассона:

1. .

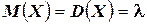Действительно: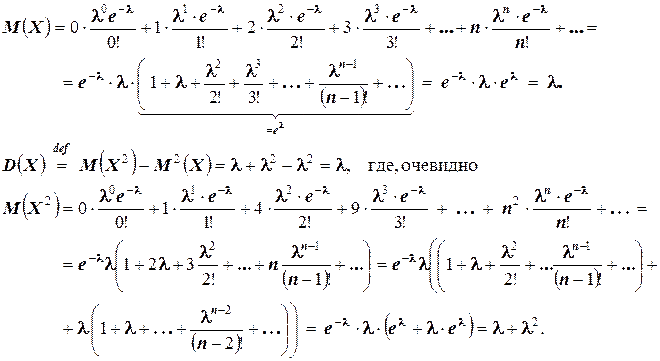

2. .

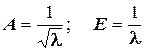3. если 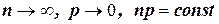, то из биномиального распределения следует закон распределения Пуассона.

ПРИМЕР 1.Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут: а) три негодных изделия; б) не более трёх повреждённых изделия.

Решение: по условию n=5000, p=0,0002. Найдём .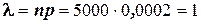

а) k = 3. Искомая вероятность по формуле Пуассона приближённо равна

.

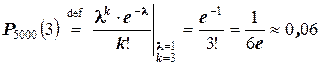б) Пусть случайная величина Х – число изделий, повреждённых в пути, то есть 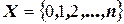. Очевидно, что данная случайная величина распределена по биномиальному закону. Следовательно, искомую вероятность можно вычислить по формуле

.

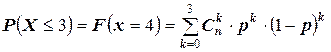Но, так как 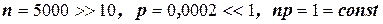, то по свойству 3^о можем воспользоваться законом распределения Пуассона, то есть, можем записать:

.

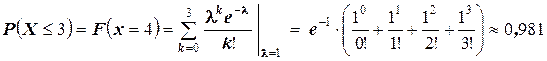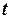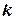Замечание.По формуле Пуассона можно вычислить вероятность того, что число событий, происшедших за время равно , если события образуют пуассоновский поток, причём 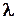– интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:

.

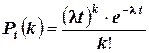ПРИМЕР 2. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течении которых телефонистка отлучилась, не будет ни одного вызова?

Решение: Найдём, прежде всего, 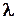– среднее число вызовов за 1 секунду:

.

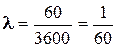Тогда, при 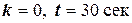, получим:

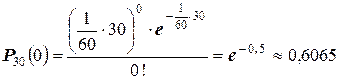
23.*Геометрическое распределение, его определение, свойства и примеры.

Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 - p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k - 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k - 1 неудач, а в k-ое испытание — удача, равна 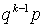. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность 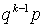. Этот закон распределения и называется геометрическим распределением . Название происходит из того, что величина 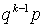представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать: 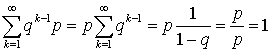, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем: 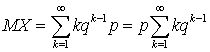. Для вычисления суммы воспользуемся следующим приемом — заменим 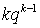на 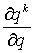и вынесем производную за знак суммы, в итоге получим: 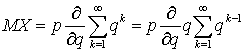. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна 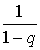. Вычисляя производную, запишем: 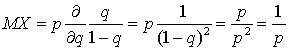. Аналогично можно получить выражение для 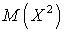: 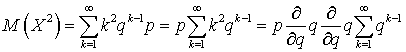. Заменяя сумму на ее значение 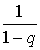, вычисляем: 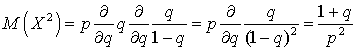. Таким образом, имеем выражение для дисперсии: 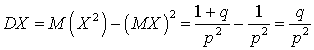. Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).Пример 30.1Вероятность попадания в мишень из винтовки равна 0,8. Найти математическое ожидание и дисперсию случайной величины — количества выстрелов до первого попадания.Математическое ожидание 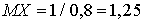, дисперсия 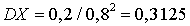. Полученные результаты означают, что при вероятности попадания 0,8 попадание будет в среднем с 1—2 выстрела.

24.Равномерный закон распределения, его определение, свойства и примеры.
Законы распределения НСВ
Плотности распределения НСВ называют также законами распределения. Часто встречаются законы равномерного, нормального и показательного распределений.

Определение.1. Закон распределения НСВ 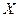называется равномерным, если ее плотность распределения задается в виде:

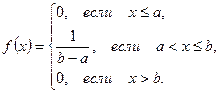
1. Зная плотность распределения, и используя формулу ,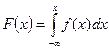

можно найти функцию распределения:

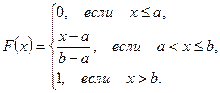
2. Если НСВ 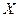имеет равномерное распределение, то ее числовые характеристики могут быть найдены по формулам:

.

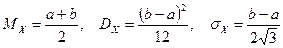3. Вероятность попадания равномерно-распределенной НСВ 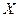в интервал 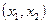можно определить по формуле:

.

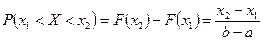Пример 1. Автобусы подходят к остановке с интервалом в 5 минут. Считая, что НСВ 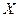- время ожидания автобуса - распределена равномерно, найти среднее время ожидания (математическое ожидание), среднее квадратическое отклонение. Какова вероятность того, случайно подошедший на остановку пассажир будет ожидать автобус не более 4 минут, но и не менее 2 минут.

Решение:

;

.
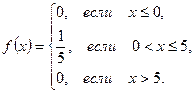
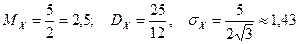
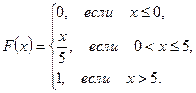
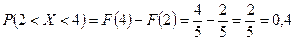