Оценка точности результатов измерений по значениям невязок фигур и свободных членов синусных условий
Качество угловых измерений в триангуляции характеризуется средней квадратической ошибкой измеренного угла, вычисляемой по невязкам треугольников и синусных условий. Для этого по приведенным к центрам пунктов и на плоскость в проекции Гаусса-Крюгера направлениям вычисляют углы в треугольниках и подсчитывают их невязки (табл. 8) по формуле (4).
Предельные невязки в треугольниках, вычисляемые по формуле
,
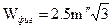не должны превышать ± 20˝при средней квадратической ошибке измерения углов в триангуляции данного класса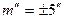 
.
Среднюю квадратическую ошибку измерения угла по невязкам треугольников вычисляют по формуле Ферерро :
,
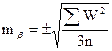где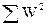 
- сумма квадратов невязок треугольников , n – число треугольников.
К синусным относят полюсные и базисные условия, возникающие в сети триангуляции.
Полюсные условия возникают в центральных системах и там, где в сети имеются диагонали (геодезические четырехугольники).
В данной сети полюсное условие возникает в центральной системе с полюсом на пункте 7. Свободные члены этого условия вычислены в таблице 9.
Таблица 8
Вычисление невязок треугольников
| № треуголь-ника | Назв. верш. | Угол | W, сек | № треуголь-ника | Назв. верш. | Угол | W, сек | ||||
| ° | ¢ | ² | ° | ¢ | ² | ||||||
| 52,3 | 47,1 | ||||||||||
| I | 13,9 | IV | 46,7 | ||||||||
| 57,0 | 21,8 | ||||||||||
| S | 03,2 | +3,2 | S | 55,6 | -4,4 | ||||||
| 10,3 | 21,2 | ||||||||||
| II | 51,4 | V | 57,0 | ||||||||
| 59,6 | 43,6 | ||||||||||
| S | 01,3 | +1,3 | S | 01,8 | +1,8 | ||||||
| 57,2 | 22,8 | ||||||||||
| III | 35,9 | VI | 16,2 | ||||||||
| 27,4 | 17,5 | ||||||||||
| S | 00,5 | +0,5 | S | 56,5 | -3,5 |
.
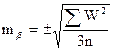
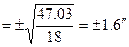Полюсное условие, выраженное через синусы углов, имеет вид:
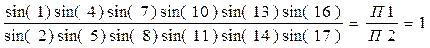. (8)
Свободный член полюсного условия вычисляется по формуле:
,
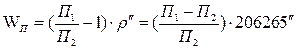где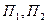 
- соответственно, произведения синусов углов числителя и знаменателя дроби полюсного условия, не должен превышать значения 
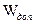, которое вычисляется по формуле:
.
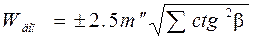Пример.
.
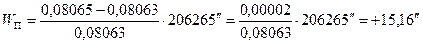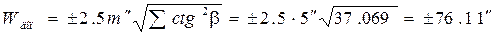
Базисное условие возникает в сети триангуляции, если имеются две или более стороны, длины которых известны (измерены или вычислены по известным координатам). В сети триангуляции, изображенной на рис. 1.1, известны длины базисных сторон между пунктами 2-3 -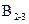 
и пунктами 4-5 - 
.
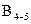Для составления базисного условия вычисляют по теореме синусов последовательно связующие стороны треугольников II, III, IV, начиная от известной стороны :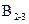
; 
; 
.
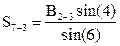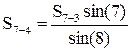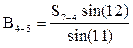После объединения формул в одну получаем :
.
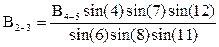Свободный член базисного условия, вычисляемый по формуле
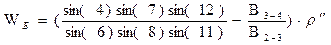, (9)
не должен превышать допустимого значения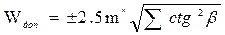 
.
Вычисления представлены в таблице 10.
В том случае, когда свободный член какого либо условного уравнения не удовлетворяет установленным допускам, необходимо выявить и устранить причины, приведшие к недопустимой величине.
Если угловые измерения в сети не содержат недопустимых ошибок, выполнены качественно и удовлетворяют предъявляемым к ним требованиям, можно приступать к окончательному уравниванию сети триангуляции.
Таблица 9
| Вычисление коэффициентов и свободного члена полюсного условного уравнения | |||||||||
| Угол при вершине треугольника | Значение угла ° ¢ ² | Sin β | ctg β | ctg2 β | |||||
| 57,0 | 0,47484 | +1,853 | 3,435 | ||||||
| 59,6 | 0,97305 | -0,237 | 0,056 | ||||||
| 27,4 | 0,99184 | +0,129 | 0,017 | ||||||
| 21,8 | 0,98593 | -0,170 | 0,029 | ||||||
| 43,6 | 0,38100 | +2,427 | 5,889 | ||||||
| 17,5 | 0,46852 | +1,886 | 3,556 | ||||||
| Числитель П1= | 0,08065 | ||||||||
| 52,3 | 0,79563 | +0,761 | 0,580 | ||||||
| 51,4 | 0,21015 | +4,652 | 21,644 | ||||||
| 57,2 | 0,74933 | +0,884 | 0,781 | ||||||
| 47,1 | 0,77490 | +0,816 | 0,665 | ||||||
| 21,2 | 0,87216 | -0,561 | 0,315 | ||||||
| 22,8 | 0,95225 | +0,321 | 0,103 | ||||||
| Знаменатель П2= | 0,08063 | ||||||||
| WП= | +51,16² | [ctg2β]= | 37,069 | ||||||
| Wдоп= | ±76,11² | ||||||||
Вывод: Значение невязки полюсного условия не превосходит допустимого значения.
Таблица 10