Минимизация по методу Квайна с применением карт Карно
Минимизация по методу Квайна с применением карт Карно сводится к следующим этапам:
1. Нанесение функции на карту Карно.
2. Анализ каждой клетки с «единицей» и нахождение для нее простых и существенных импликант. Если найдена существенная импликанта, то клетки с «единицами», составляющие эту импликанту, при дальнейшем поиске простых импликант не рассматривают. Для этого их отмечают точками. Поэтому при рассмотрении карт Карно необходимо прежде всего обнаружить клетки с «единицами», которые дают существенные импликанты. Это уменьшает количество рассматриваемых клеток с «единицами».
3. Исключение существенных импликант и накрываемых ими конституент единицы функции из дальнейшего рассмотрения.
4. Как и по методу Квайна составляется импликантная таблица, строки которой обозначаются простыми импликантами, полученными на этапе 2, а столбцы – конституентами единицы, оставшимися после выполнения этапа 3.
Дальнейший порядок минимизации функции такой же, как и по методу Квайна. Однако в большинстве случаев по виду карт Карно можно определить простые импликанты, которые накрывают клетки с «единицами» без точек (см. этап 2). Приведем пример минимизации ФАЛ четырех переменных, применяя карты Карно для нахождения простых и существенных импликант функции и преобразование Петрика для нахождения тупиковых минимальных форм аналитическим способом.
Пример 7. Найти минимальную ДНФ функции f(х4, х3, х2, х1), которая равна единице на наборах переменных: 2, 3, 4, 5, 7, 9, 11, 12, 13.
Решение.
1. Нанесем заданную ФАЛ на карту Карно (рис. 4,а).
Рис. 4. Карты Карно ФАЛ четырех переменных
2.Найдем простые и существенные импликанты функции.
Конституента единицы 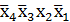 склеивается только с соседней конституентой единицы
склеивается только с соседней конституентой единицы 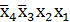 по переменной
по переменной 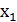 . В результате получим простую импликанту
. В результате получим простую импликанту 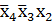 , которая является также существенной. Отметим клетки этих конституент единицы, составляющих существенную импликанту, точками. В дальнейшем к клеткам с точками обращаться не нужно.
, которая является также существенной. Отметим клетки этих конституент единицы, составляющих существенную импликанту, точками. В дальнейшем к клеткам с точками обращаться не нужно.
Клетка конституенты единицы 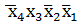 образует квадрат с тремя клетками, содержащими единицы. В результате склеивания четырех конституент единицы этих клеток получим существенную импликанту
образует квадрат с тремя клетками, содержащими единицы. В результате склеивания четырех конституент единицы этих клеток получим существенную импликанту 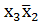 . Отмечаем эти четыре клетки этих конституент единицы точками.
. Отмечаем эти четыре клетки этих конституент единицы точками.
Конституента единицы 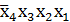 склеивается с соседними сверху и слева. В результате получим простые импликанты
склеивается с соседними сверху и слева. В результате получим простые импликанты 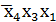 и
и 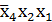 .
.
Конституента единицы 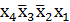 склеивается с соседними слева и снизу. В результате получим простые импликанты
склеивается с соседними слева и снизу. В результате получим простые импликанты 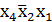 и
и 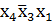 .
.
Конституента единицы 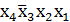 склеивается с соседними сверху и с крайней в строке. В результате получим простые импликанты
склеивается с соседними сверху и с крайней в строке. В результате получим простые импликанты 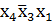 и
и 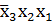 .
.
Таким образом простыми импликантами являются 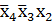 ,
, 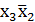 ,
, 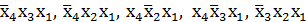 , дизъюнкция которых есть сокращенная ДНФ функции. Простые импликанты
, дизъюнкция которых есть сокращенная ДНФ функции. Простые импликанты 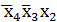 ,
, 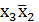 являются также существенными, которые обязательно войдут в минимальную ДНФ функции. Поэтому существенные импликанты функции и входящие в них конституенты единицы в составлении импликантной таблицы не участвуют.
являются также существенными, которые обязательно войдут в минимальную ДНФ функции. Поэтому существенные импликанты функции и входящие в них конституенты единицы в составлении импликантной таблицы не участвуют.
3. Составим импликантную таблицу (табл. 5), столбцы и строки которой озаглавим оставшимися конституентами единицы и простыми импликантами соответственно, и расставим метки.
Таблица 5
| Конституента Простая единицы импликанта | 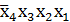 | 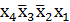 | 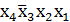 |
А = 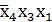 | * | ||
B = 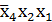 | * | ||
C = 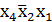 | * | ||
D = 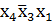 | * | * | |
E = 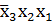 | * |
4. Нахождение тупиковых и минимальных ДНФ функции.
