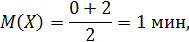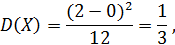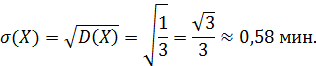Показательный (экспоненциальный закон распределения)

Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:

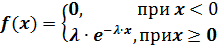
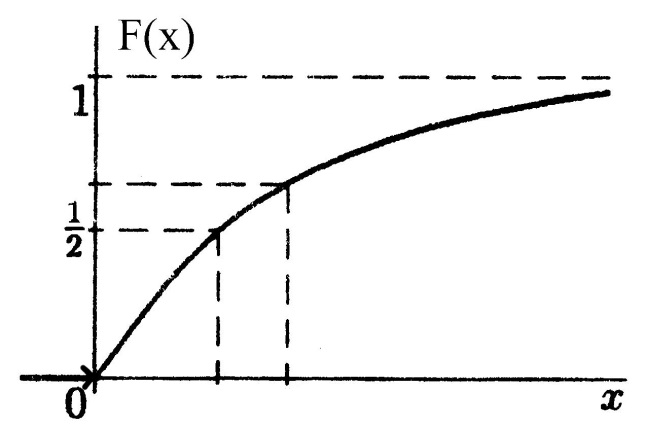
Функция распределения имеет вид:

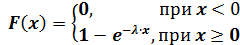
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:

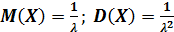
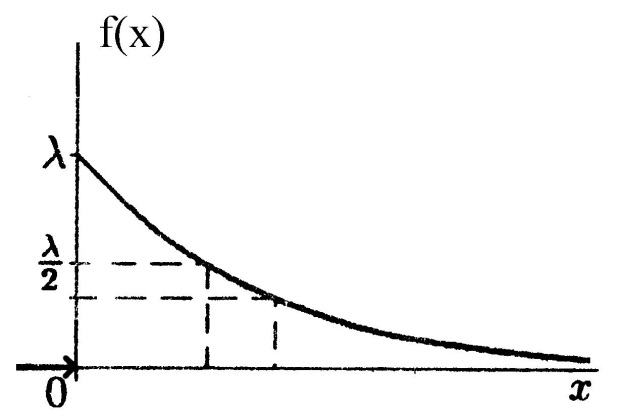
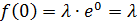
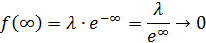
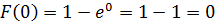
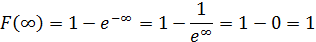
То есть при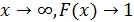

Пример.

Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.

Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.

Решение:

По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:

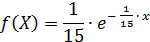
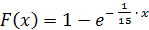
(х ≥0)

Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть

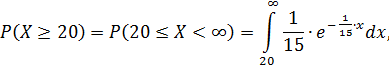но проще это сделать, используя функцию распределения:

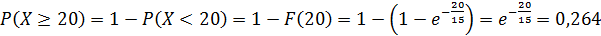
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.

Равномерный закон распределения.

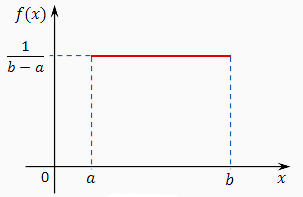
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть

f (x) имеет вид:

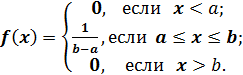
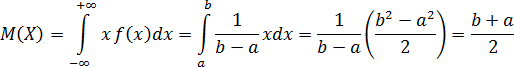
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.

Дисперсия имеет вид:

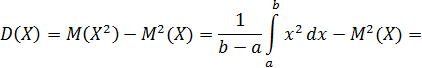
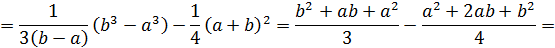
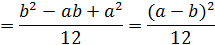
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал 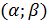, принадлежащий целиком отрезку [a, b]:

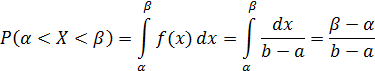
Следовательно,

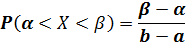
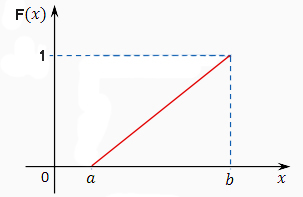
Функция распределения примет вид:

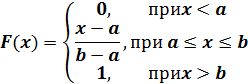
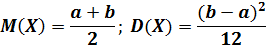
Пример.

Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.

Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.

Решение:

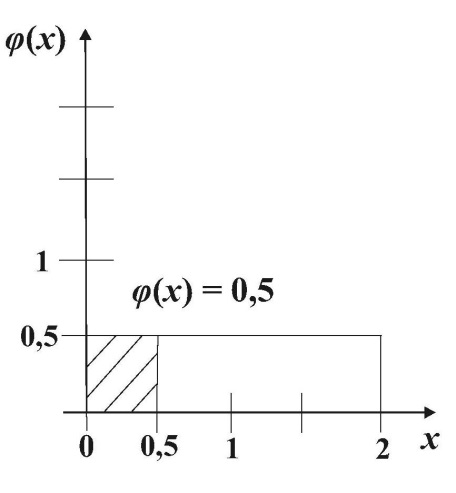
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.

Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.

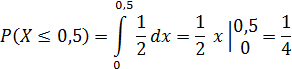
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение: