Алгоритм решения задачи. Для построения имитационной модели в Excel создадим таблицу

Для построения имитационной модели в Excel создадим таблицу, приведенную в приложении 2.

1. Все параметры задачи необходимо привести к одной размерности, т.е. выразить в сопоставимых величинах. В нашей задаче в качестве единицы времени выберем размерность «минута». Получим:

λ=18 заявок/час=0,3 заявки/мин;

μ=1/ 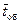=0,1 заявок/мин.

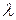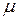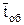Введите значения , и в ячейки F1, I1 и L1 соответственно.

2. В строке 2 таблицы получим выборку из 20 равномерно распределенных псевдослучайных чисел при помощи функции СЛЧИС(). Функция СЛЧИС() имеет следующую особенность: при нажатии клавиши F9 на клавиатуре, в ячейках, в которых введена функция СЛЧИС() генерируется новая реализация равномерно распределенных чисел. Получите 2 такие выборки по 20 значений в каждой и скопируйте их во 3-ю и 4-ю строки рабочей таблицы. При копировании из буфера обмена воспользуйтесь функцией Специальная вставка/Вставить значения.

3. В строке 5 получим интервалы времени 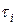между приходом клиентов. Для этого необходимо преобразовать выборку равномерно распределенных чисел из строки 3 в выборку, имеющую показательный закон распределения по формуле (6). В Excel, в ячейке С7 введите формулу:

= - (1/F1)*LN(С5).

Полученные значения необходимо округлить до ближайшего большего целого числа (см. пример 2). Для того чтобы округлить значения до ближайшего большего целого используйте встроенную функцию ОКРВВЕРХ(). В ячейке С7 должна быть формула:

=ОКРВВЕРХ(- (1/$F$1)*LN(С5);1).

4. В строку 6 заносится время поступления заявок, ранжированное в порядке возрастания (кумулятивным образом). Время поступления первой заявки равно значению в ячейке С7. Время поступления второй и последующих заявок получаем по формуле .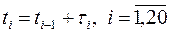

В ячейку D8 введите формулу =C8+D7, и скопируйте ее до конца строки.

5. Длительность обслуживания заявок 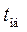является случайной величиной, распределенной по показательному закону с параметром 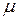. Для получения продолжительностей обслуживания заявок используем формулу:

,

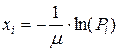где 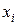- случайные числа, имеющие показательный закон распределения; 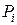- равномерно распределенные случайные числа из строки 4. Полученные значения округлим до ближайшего большего целого числа для удобства дальнейшей работы с таблицей. В ячейке С9 введите формулу:

=ОКРВВЕРХ(-1/$I$1*LN(C6);1).

6. В строках 8 и 10 расчетной таблицы реализуется логическая функция принятия решения о приеме заявки на обслуживания либо отказе:

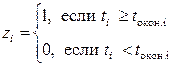. (19)

Переменная 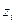– это булева (двоичная) переменная, которая может принимать только два значения: 1 либо 0. Значение 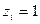имеет смысл: «данный канал свободен и заявка, поступившая в момент времени 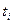принимается на обслуживание»; 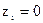означает отказ в приеме заявки (канал занят, и заявка передается в другой канал). Если оба канала заняты ( 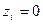), то согласно условию задачи (система с отказами) заявка покидает СМО, и счетчик отказов 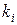(строка 12) принимает значение 1, в противном случае, когда заявка принята на обслуживание в один из каналов, .

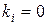7. В строках 9 и 11 таблицы необходимо указать время окончания обслуживания поступивших на данный канал заявок.

8. Оценка вероятности отказа в обслуживании находится по формуле:

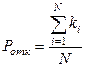. (20)

Анализ решения. Если вероятность отказа в обслуживании, рассчитанная по формуле (20), велика, то это означает, что СМО работает неэффективно и необходимо либо увеличить количество каналов обслуживания, либо попытаться сократить среднее время обслуживания заявок.

Проведем 3 серии вычислительных экспериментов по 10 прогонов в каждом, меняя среднее время обслуживания заявок в системе и проанализируем как это отразится на оценке вероятности отказа в обслуживании.

Замечание. Для того, чтобы сократить время проведения вычислительных экспериментов и автоматизировать процесс подсчета числа отказов можно использовать логические встроенные функции Excel: ЕСЛИ(), И(), ИЛИ(). Эти функции используются для автоматического заполнения строк №№ 8, 9, 10, 11 и 12 табличной имитационной модели.

Результаты вычислительных экспериментов приведены в таблице 5.

Таблица 5. Вероятность отказа в обслуживании при разных значениях .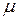

Номер эксперимента											Средние
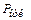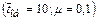	0,15	0,7	0,55	0,5	0,6	0,45	0,3	0,45	0,45	0,4	0,45
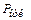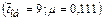	0,35	0,35	0,35	0,65	0,45	0,6	0,6	0,35	0,35	0,25	0,43
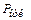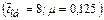	0,4	0,5	0,35	0,2	0,4	0,55	0,5	0,5	0,45	0,25	0,41

Из таблицы видно, что средняя вероятность отказа в обслуживании при 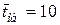равна 0,45.

Сравним результат, полученный в результате имитации с аналитическим решением, которое можно найти, используя формулу (9):

, ,

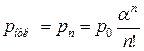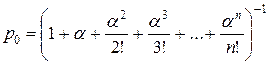где 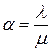- нагрузка на систему.

Для текущей задачи 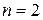, 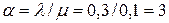. Вероятность отказа в обслуживании будет равна:

,

.

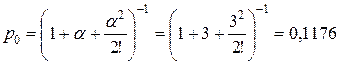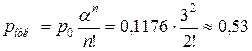Полученное аналитическое решение отличается от результата, полученного методом статистического моделирования. Объяснить это можно тем, что в имитационной модели присутствует элемент случайности.

Замечание. При неограниченном росте числа требований ( 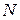) результаты имитации должны сходиться с аналитическим решением данной задачи.

Полученное в результате вычислительного эксперимента значение 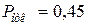означает, что в среднем 9 из 20 поступившихся в систему заявок получают отказ. То есть СМО работает недостаточно эффективно. Уменьшить вероятность отказа можно либо добавив 3-й канал обслуживания, либо уменьшив 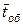. При уменьшении среднего времени обслуживания заявок, интенсивность потока обслуженных заявок 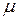растет, и меньшее количество поступивших заявок получает отказ. Соответственно, вероятность отказа в обслуживании снижается.

Полученную табличную имитационную модель можно использовать для имитации работы любых двухканальных СМО. При этом случайные параметры СМО (время поступления требований и время обслуживания) могут иметь любой закон распределения. Для моделирования случайных величин с заданным законом распределения можно воспользоваться инструментом Excel Анализ данных / Генерация случайных чисел.

Меняя значения параметров 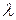, 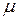и 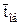можно подобрать такие характеристики СМО, при которых вероятность отказа в обслуживании будет приемлемой.

Кроме того, полученную табличную модель несложно модифицировать, добавив дополнительные каналы обслуживания.