D) если они лежат на одной прямой или на параллельных прямых

D) они имеют одинаковые размеры и их соответствующие элементы равны

3.1. При транспонировании квадратной матрицы, определитель

D) не меняется

4.1. Найти произведение матрицы А на число a А= 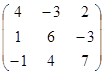, a= 2

C)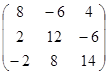

5.1. Найти разность двух матриц 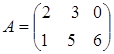и

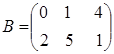
A)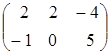

6.1. Найти сумму матриц А= 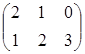и В=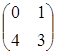

D) не существует

7.1. Умножить матрицу А= 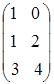на матрицу В=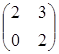

D)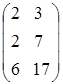

8.1. Какое произведение матриц АВ не имеет смысла?

D)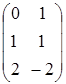

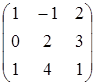
9.1. Укажите матрицу, транспонированную матрице А=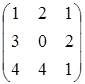

B)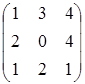

10.1. Вычислить определитель:

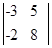
D)-14

11.1. Вычислить определитель:

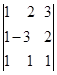
D) 9

12.1. Минором 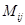матрицы n-го порядка называется определитель (n-1)-го порядка полученный в результате :

A) вычеркивания i-й строки и j-го столбца

13.1. Дана матрица А= 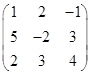. Найти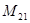

A)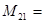

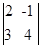
13.2. Дана матрица А= 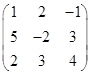. Найти .

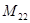C) 6

13.3. Дана матрица А= 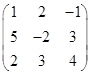. Найти .

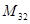B)8

13.4. Найти минор элемента 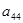, если матрица имеет вид: А=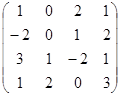

D)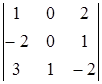

14.1. Алгебраическим дополнением элемента 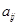называется число:

E)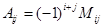

15.1. Найти алгебраическое дополнение элемента 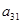матрицы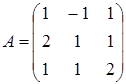

B)-2

16.1. Если |А|=0, то квадратная матрица называется

A) вырожденной

17.1. Квадратная матрица А^–1 называется обратной к матрице А, если

выполняется условие:

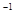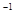С) А ·А =А ·А=Е

18.1. Найти вырожденную матрицу:

D)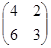

19.1.Найдите |AB–4E|, если A= 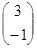, B = (2 -1)

D)-12

20.1.Наивысший порядок отличных от нуля миноров матрицы называется

C) рангом матрицы

21.1.Диагональная матрица у которой каждый элемент находящийся на главной диагонали равен единице называется

C) единичной

22.1.Матрица все элементы которой равны нулю называется

D) нулевой

23.1.Матрица, имеющая n строк и n столбцов называется

B) квадратной

24.1. Квадратная матрица у которой равны нулю все её элементы, стоящие ниже (или выше) главной диагонали называется

A) треугольной

25.1.Квадратная матрица у которой все элементы не находящиеся на главной диагонали равны нулю называется

B) диагональной

26.1.Умножение матрицы на матрицу определено, если

E) число столбцов первой матрицы равно числу строк второй матрицы.

27.1.Система линейных уравнений совместна тогда и только тогда, когда

D) ранг расширенной матрицы системы равен рангу основной матрицы.

28.1.Если в системе линейных уравнений все свободные члены равны нулю, то система называется:

В) однородной;

29.1. Определите ранг матрицы: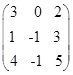

A)2

29.2. Определите ранг матрицы:

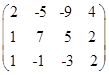
A)2

30.1. Определить параметры 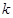и 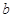прямой .

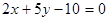В) ;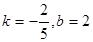

31.1. Угловой коэффициент 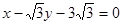прямой равен:

Е) .

31.2. Угловой коэффициент 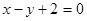прямой равен:

Д) ;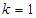

32.1. Укажите уравнение прямой, проходящей через начало координат и образующей с осью Ох угол .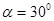

С) ;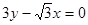

32.2. Укажите уравнение прямой, проходящей через начало координат и образующей с осью Ох угол .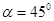

Д) ;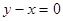

33.1. Можно ли уравнение прямой 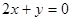записать в отрезках?

С) нет

34.1. Укажите прямую, перпендикулярную прямой .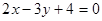

С) ;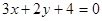

35.1. Уравнение прямой с угловым коэффициентом имеет вид:

A) y = kx+b

36.1. Общее уравнение прямой имеет вид:

C) Ax+By+C=0

37.1. Расстояние между двумя точками 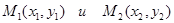определяется следующей формулой:

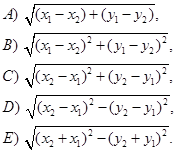С –правильный ответ

**********

38.1. Даны точки А(3;1) и В(2;1). Определить длину отрезка АВ.

A)1

39.1. Даны две смежные вершины квадрата А(4; 2) и В(6; 1). Вычислить его площадь.

C) 5

40.1. Найти координаты проекции на ось абсцисс точки А(5; -7).

A) (5; 0)

41.1.Даны вершины треугольника: А(1; 4), В(3; -9) и С(-5; 2). Определить длину его

медианы BК.

В) 13

42.1. Вычислить расстояние от точки А(-2; 3) до прямой 3х-4у–7=0.

C) 5

43.1. Составьте уравнение гиперболы, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная ,что ось 2а=16 и эксцентриситет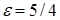

В ) х²/64-у²/36=1

44.1. Определите полуоси эллипса: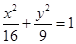

E) 4 и 3.

45.1.Каноническое уравнение эллипса имеет вид:

B)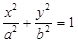

46.1.Эксцентриситетпараболы

B) е =1

47.1. Множество точек плоскости, равноудаленных от данной точки F и данной прямой d, не проходящей через точку F называется

D) параболой

48.1. Множество точек плоскости, для которых сумма расстояний до двух данных фиксированных точек (фокусов), есть величина постоянная, большая чем расстояние между фокусами называется

A) эллипсом

49.1. Какое равенство выполняется для гиперболы?

A)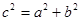

50.1. Эксцентриситет эллипса вычисляется по формуле

A)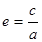

51.1.Параметрические уравнения прямой

B)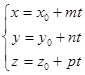

52.1. Расстояние между двумя точками в пространстве

E)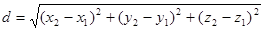

***********

53.1. Укажите уравнение плоскости, проходящей через точку 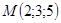и перпендикулярной вектору .

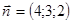A) ;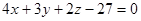

54.1.Указать общее уравнение плоскости

А) Ax+By+Cz+D=0

55.1. Условие перпендикулярности плоскостей

B) A₂ ×A₁ + B₂ ×B₁+C₂×C₁=0

56.1. Расстояние от точки до плоскости

B) d=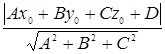

57.1.Угол между двумя плоскостями

E)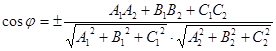

58.1.Условие перпендикулярности прямой и плоскости

B)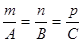

59.1. Определить расстояние от точки M₀(2; 3; -1) до плоскости 7x-6y-6z+42=0

D)4

60.1. Составить уравнение плоскости, проходящей через точку М(2;3;5) и перпендикулярной вектору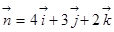

C) 4x+3y+2z-27=0

61.1. Найти угол между плоскостями 6х+2у-4z+17=0 и 9х+3у-6z-4=0

А)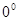

62.1. Два вектора называются коллинеарными;

D) если они лежат на одной прямой или на параллельных прямых

63.1. Модуль вектора 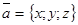вычисляется по формуле:

A)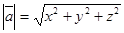

64.1. Нулевым вектором называется

В) вектор, все координаты которого равны нулю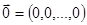

65.1. Найти разность 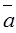- 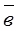, есл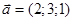и и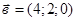

C) (-2;1;1)

66.1. Даны векторы 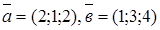. Найти их скалярное произведение (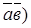

D) 13

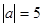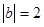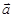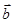67.1. Найти скалярное произведение векторов, если даны , и угол между векторами и равен .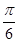

E) 5

68.1. Найдите площадь параллелограмма, построенного на векторах 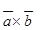, если:

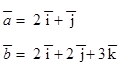
А) 7 кв.ед

69.1.Объем параллелепипеда, построенного на приведенных к общему началу векторах 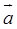, , 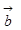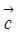равен:

A) | ( ´ )× |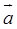

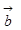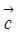70.1. Функцией у=f(x) называется

Е) формула связи переменных х и у

**********

71.1.Если для " 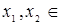Х из условия 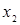> 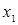следует, что 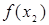> 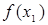, то функция называется D) убываюшей

72.1.Если выполняется условие: 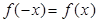, то функция называется

А) четной

73.1.Если выполняется условие: 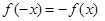, то функция называется

D) нечетной

74.1. Если существует такое число М>0, что для всех хÎ Х выполняется неравенство | 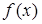|£ М, то функция называется

В) ограниченной

75.1.Если функция 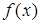определена в окрестности точк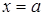и и 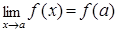, то функция 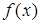в точке 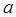называется

А) непрерывной

76.1. Найдите предел: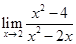

B) 2

77.1. Найдите предел: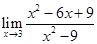

E) 0

78.1. Найдите предел: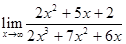

E) 0

78.2. Найдите предел: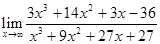

D) 3

79.1. Найдите предел: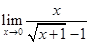

B) 2

80.1. Найдите предел: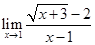

E)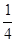

81.1. Найдите предел: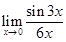

A)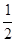

82.1. Найдите предел: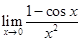

A)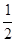

83.1. Указать второй замечательный предел:

А)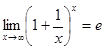

84.1. Найдите предел: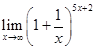

D)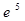

85.1. Среди следующих формул укажите неверную:

B)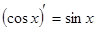

86.1. Найдите производную неявной функции: х³+х²у+у²=0

В) (3х²+2ху)/х²+2у

87.1.Если y=f(u) и u=φ(x) – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна

C)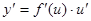

88.1.Производной функции у=f(x) в точке Х₀ называется

E)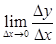

89.1.Скорость прямолинейного движения материальной точки в момент времени t есть