Засоби вимірювальної техніки
ТЕОРІЯ ЗАСОБІВ ВИМІРЮВАННЯ
Методичні вказівки
до практичних занять
для студентів напряму підготовки 6.051003 «Приладобудування»,
професійного спрямування «Прилади і системи екологічного моніторингу»
Рекомендовано вченою радою приладобудівного факультету
(протокол № від . .2016 р.)
Київ
НТУУ «КПІ»
Теорія засобів вимірювання: Методичні вказівки до практичних занять для студентів напряму підготовки 6.051003 «Приладобудування», професійного спрямування «Прилади і системи екологічного моніторингу» денної та заочної форми навчання [Текст] / Уклад.: І. В. Морозова – К.: НТУУ «КПІ», 2016. – 46 с.
Методичні вказівки призначено для студентів напряму підготовки 6.051003 «Приладобудування», професійного спрямування «Прилади і системи екологічного моніторингу» денної та заочної форми навчання. Методичні вказівки допомагають засвоїти матеріал, отриманий на лекційних заняттях та придбати навички в обробці результатів вимірювання.
Навчальне електронне мережне видання
ТЕОРІЯ ЗАСОБІВ ВИМІРЮВАННЯ
Методичні вказівки
до виконання практичних завдань
для студентів напряму підготовки 6.051003 «Прилади»,
професійного спрямування «Прилади і системи екологічного моніторингу»
Укладач: Морозова Ірина Володимирівна, ст. викладач
Відповідальний редактор: Порєв В.А., д.т.н. професор
Рецензент: Самарай В.П., к.т.н., доцент
ЗМІСТ
Загальні положення............................................................................................ 4
Практичне заняття № 1. Вимірювані величини, їх значення та одиниці……………...……...……………...……………………………...……...…..5
Практичне заняття № 2.Засоби вимірювальної техніки ………………………………………………………………………………………...9
Практичне заняття № 3. Характеристики якості вимірювань. Похибки вимірювань …………………………………………………………………………11
Практичне заняття № 4. Систематичні, прогресуючі та регулярні похибки ……………………………………………………………………………………………….15
Практичне заняття № 5. Випадкові похибки..…...…………………………… …18
Практичне заняття № 6. Адитивна, мультиплікативна та нелінійна похибки ………………………………………………………………………..……………...31
Практичне заняття № 7. Інструментальні похибки………………………..……..35
Перелік літератури………………………………………...………………………..45
ЗАГАЛЬНІ ПОЛОЖЕННЯ
У 5-му семестрі з навчальної дисципліни «Теорія засобів вимірювання» проводяться практичні заняття, підготовка до яких здійснюється за рахунок часу відведеного на самостійну роботу студента.
Метою практичних занять з курсу „Теорія засобів вимірювання” є ознайомлення студентів з основними поняттями і визначеннями, закріплення теоретичного матеріалу з дослідження методів визначення похибок, методу збігу вимірювання розмірів виробів або окремих їх елементів, дослідження нормованих метрологічних характеристик різних приладів, класу точності засобу вимірювання, помилок в результатах вимірювань фізичних величин методом найменших квадратів.
Підготовка до практичного заняття полягає в досконалому вивченню теоретичної частини і закінчується виконанням завдання. До проведення практичного заняття викладач проводить співбесіду зі студентом, який чітко проявляє знання мети роботи та основні теоретичні відомості.
Практичне заняття №1
ВИМІРЮВАНІ ВЕЛИЧИНИ, ЇХ ЗНАЧЕННЯ ТА ОДИНИЦІ
Теоретичні відомості
Сукупність величин, серед яких одні умовно вважаються незалежними, а інші на основі фізичних законів виражаються через них, називають системою величин. Незалежні величини цієї системи називаються основними, а всі інші — похідними величинами. Відповідно одиниці основних величин називають основними одиницями, похідних величин — похідними одиницями. Сукупність основних і похідних одиниць становить систему одиниць.
Міжнародна система одиниць задовольняє такі важливі вимоги, як:
- невелика кількість основних одиниць (7 та 2 додаткові);
- основні одиниці порівняно легко відтворюються з високою точністю;
- основні одиниці мають такі розміри, що числові значення більшості величин виражаються не надто малими і не надто великими числами;
- похідні одиниці є когерентними, тобто входять у рівняння, що пов’язують їх з іншими одиницями, з коефіцієнтом, що дорівнює одиниці.
Одиниці, що не входять в систему одиниць, називають позасистемними одиницями. їх використання зумовлено історичними традиціями, наприклад, одиниці довжини — дюйм, фут, ярд, миля тощо, одиниці тиску — атмосфера, міліметр ртутного стовпчика, одиниця потужності — кінська сила тощо.
Відносні одиниці — це:
- відсоток (процент), % — одна сота значення величини (10-2);
- проміле ‰ — одна тисячна значення величини (10-3);
ррт (читати „пі-пі-ем”) — одна мільйонна значення величини (1ррт — = 1/106 = 10-6).
Позасистемні одиниці, що визначаються як логарифм відношення двох однорідних величин, називаються логарифмічними одиницями: Бел (Б), децибел (дБ), октава (окт), декада.
Для значень потужності чи енергії 1 бел визначається за виразом
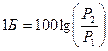 , (1.1)
, (1.1)
тобто 100 белам відповідає відношення (зміна) потужності у 10 разів, а одному белу відповідає зміна потужності сигналу 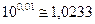 рази.
рази.
На практиці частіше використовують у десять разів меншу одиницю—децибел
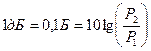 , (1.2)
, (1.2)
10 децибелам відповідає те саме відношення (зміна) потужності у 10 разів, а одному децибелу відповідає зміна потужності сигналу 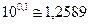 раз.
раз.
Для значень сигналів (наприклад, напруги 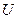 , струму І) один децибел є вдвічі більшим і визначається за виразом
, струму І) один децибел є вдвічі більшим і визначається за виразом
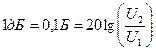 . (1.3)
. (1.3)
Тобто зміні (відношенню) сигналу у 10 разів відповідає 20 дБ, у 100 разів — 40 дБ тощо.
Якщо задано відношення (зміна) величин у децибелах ( 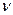 , дБ), то у звичайних одиницях воно становить
, дБ), то у звичайних одиницях воно становить
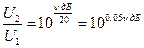 . (1.4)
. (1.4)
У разі зміни (відношення) частот використовуються інші логарифмічні одиниці: октава і декада.
Одна октава — це зміна частоти вдвічі, тобто у такому разі застосовується логарифм з основою 2
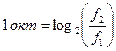 . (1.5)
. (1.5)
Отже, наприклад, три октави — це зміна частоти у 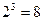 разів. Одна декада — це зміна частоти у десять разів, тобто у такому разі використовується логарифм з основою 10, але без співмножника
разів. Одна декада — це зміна частоти у десять разів, тобто у такому разі використовується логарифм з основою 10, але без співмножника
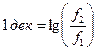 . (1.6)
. (1.6)
Отже, наприклад, дві декади — це зміна частоти у 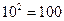 разів.
разів.
Розмірність (англ. dim. — dimension) основної величини — це її позначення. Тобто розмірність маси — М, розмірність часу — Т, розмірність довжини — 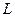 , розмірність сили струму —
, розмірність сили струму — 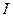 , розмірність термодинамічної температури —
, розмірність термодинамічної температури — 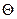 , розмірність кількості речовини —
, розмірність кількості речовини — 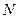 , розмірність сили світла —
, розмірність сили світла — 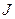 .
.
Отже, розмірності фізичних величин є водночас розмірностями їх одиниць. Розмірність похідної величини — це вираз, що описує її зв'язок а основними величинами системи і становить добуток розмірностей основних величин, піднесених до відповідного степеня 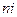
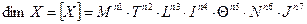 . (1.7)
. (1.7)
Утворюючи формули розмірностей похідних величин, загалом використовують такі правила:
1. Якщо значення величини С дорівнює добутку значень величин А і В ( 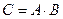 ),то розмірність величини С дорівнює добутку розмірностей А і В:
),то розмірність величини С дорівнює добутку розмірностей А і В:
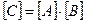 . (1.8)
. (1.8)
Тобто нехай, наприклад,
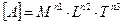 та
та 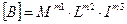 , (1.9)
, (1.9)
тоді
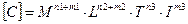 . (1.10)
. (1.10)
2. Якщо значення величини С дорівнює відношенню значень величин А і В ( 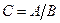 ), то розмірність величини С дорівнює відношенню розмірностей А і В:
), то розмірність величини С дорівнює відношенню розмірностей А і В:
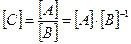 . (1.11)
. (1.11)
Тобто для розмірностей (11) розмірність С
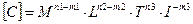 . (1.12)
. (1.12)
3. Якщо значення величини С дорівнює степеню 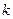 значення величини А (
значення величини А ( 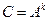 )то розмірність величини С дорівнює степеню
)то розмірність величини С дорівнює степеню 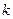 розмірності А:
розмірності А:
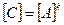 . (1.13)
. (1.13)
Тобто для розмірності А за виразом (13) розмірність С
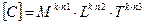 . (1.14)
. (1.14)
Задача 1.Подати значення 0,005 % у проміле та ррm.
Розв’язання. 1. Перетворимо відсотки у відносне значення
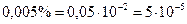 .
.
2. Перетворимо отримане значення у проміле
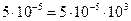 ‰=0,05‰.
‰=0,05‰.
3. Перетворимо одержане значення у ррm
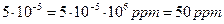 .
.
Задача 2. Коефіцієнт підсилення сигналу становить 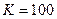 разів. Падати значення коефіцієнта у децибелах
разів. Падати значення коефіцієнта у децибелах 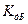 .
.
Разв’язання. За (1.3) 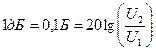 коефіцієнт підсилення як відношення напруги на виході до напруги на вході в децибелах дорівнює Кдб=20lg(K)=20lg(100)=40дб
коефіцієнт підсилення як відношення напруги на виході до напруги на вході в децибелах дорівнює Кдб=20lg(K)=20lg(100)=40дб
Задача 3.Діапазон частот аналізатора спектра сигналу простягається від частоти 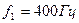 до частоти
до частоти 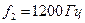 . Подати значення відносного діапазону частот
. Подати значення відносного діапазону частот 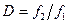 в октавах.
в октавах.
Разв’язання. За (1.5) 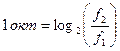 відносний діапазон частот в октавах дорівнює
відносний діапазон частот в октавах дорівнює 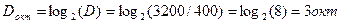

Задача 4.Коефіцієнт підсилення підсилювача зменшується на 40 децибел зі збільшенням частоти сигналу на одну декаду (пишуть 40 дБ/дек). У скільки разів зміниться підсилення, якщо частота зміниться у 100 разів ?
Розв’язання. Відповідно до (1.6) 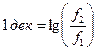 зміна частоти у 100 разів у логарифмічних одиницях становить
зміна частоти у 100 разів у логарифмічних одиницях становить 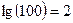 декади.
декади.
Оскільки за умовою на одну декаду підсилення змінюється на 40 дБ, то зі зміною частоти на 2 декади підсилення зміниться на
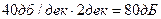
Отже, відповідно до (1.4) 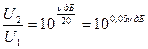 зміна коефіцієнта підсилення становить
зміна коефіцієнта підсилення становить
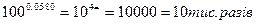
Задача 5. Знайти розмірність електричного заряду.
Разв’язання. За означенням заряд дорівнює добутку сили струму на час
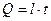
тому, використовуючи властивість (1.7), розмірність заряду описуємо виразом
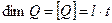
Задача 6. Встановити розмірність сили.
Розв’язання. Оскільки сила 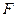 — це добуток маси тіла
— це добуток маси тіла 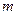 на його прискорення
на його прискорення 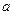
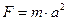
а прискорення, своєю чергою, дорівнює відношенню відстані до квадрата часу 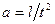 . Тому, застосовуючи властивості (1.8)
. Тому, застосовуючи властивості (1.8) 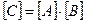 , (11)
, (11) 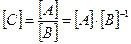 та (13)
та (13) 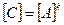 , розмірність сили описуємо виразом
, розмірність сили описуємо виразом
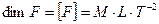
Задача 7. Знайти розмірність напруженості електричного поля.
Розв’язання. За означенням напруженість електричного поля дорівнює відношенню сили 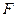 до. заряду
до. заряду 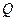 , поміщеного в електричне поле
, поміщеного в електричне поле
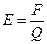
Тому, використовуючи властивість (11) 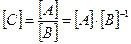 , а також одержану в прикладі 5 розмірність заряду і у прикладі 6 розмірність сили, розмірність Напруженості описуємо виразом
, а також одержану в прикладі 5 розмірність заряду і у прикладі 6 розмірність сили, розмірність Напруженості описуємо виразом
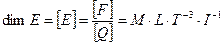
Задача 8.Визначити розмірність електричної напруги.
Розв’язання. За означенням електрична напруга між двома точками дорівнює добутку напруженості 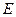 електричного поля на відстань
електричного поля на відстань 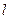 між цими точками
між цими точками
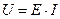
Тому, застосовуючи властивість (1.8) 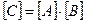 , а також одержану в задачі 7 розмірність напруженості електричного поля, розмірність напруги описуємо виразом
, а також одержану в задачі 7 розмірність напруженості електричного поля, розмірність напруги описуємо виразом
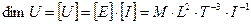
Задача 9.Знайти розмірність густини струму як відношення сили струму 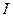 до площі
до площі 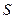 , через яку протікає струм:
, через яку протікає струм: 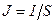 .
.
Разв’язання. Оскільки розмірність площі дорівнює квадрату розмірності довжини, тобто 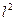 , то, використовуючи властивості (1.8)
, то, використовуючи властивості (1.8) 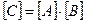 , (11)
, (11) 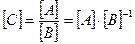 та (13)
та (13) 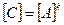 , знаходимо розмірність густини струму
, знаходимо розмірність густини струму
Практичне заняття №2
ЗАСОБИ ВИМІРЮВАЛЬНОЇ ТЕХНІКИ
Теоретичні відомості
Показом 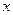 (чи
(чи 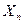 ) ЗВТ (вимірювального приладу, багатозначної міри) називають значення вимірюваної або відтвореної величини
) ЗВТ (вимірювального приладу, багатозначної міри) називають значення вимірюваної або відтвореної величини 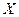 , яке визначене за допомогою його відлікового пристрою у вигляді шкали з вказівником, цифрового табло тощо.
, яке визначене за допомогою його відлікового пристрою у вигляді шкали з вказівником, цифрового табло тощо.
Шкала ЗВ — сукупність позначок (відміток) і проставлених біля деяких з них чисел відліку або інших символів, що відповідають ряду послідовних значень величини, в одиницях якої отримують покази. Якщо довжина поділок (відстань між осями сусідніх позначок) є сталою вздовж всієї шкали, то така шкала є рівномірною. Шкала з поділками різної довжини називається нерівномірною (нелінійною)
Відлік є абстрактним (неіменованим) числом ( 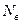 ), зчитаним з відлікового пристрою або отриманим підрахунком послідовних позначок чи сигналів.
), зчитаним з відлікового пристрою або отриманим підрахунком послідовних позначок чи сигналів.
Найбільше число, яке можна зчитати з відлікового пристрою, називається максимальним відліком 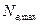 .
.
Ціпа поділки ЗВ ( 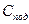 )дорівнює різниці значень величини
)дорівнює різниці значень величини 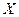 , тобто двом сусіднім позначкам шкали
, тобто двом сусіднім позначкам шкали 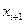 та
та 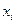 .
.
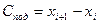 . (2.8)
. (2.8)
Сталу ЗВ визначають як відношення границі вимірювання приладу або максимального значення багатозначної міри 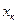 (напруги
(напруги 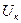 , струму
, струму 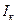 , потужності
, потужності 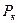 тощо) до максимального відліку
тощо) до максимального відліку 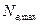 і є іменованим числом в одиницях величини
і є іменованим числом в одиницях величини 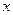 :
:
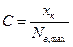 . (2.9)
. (2.9)
Показ 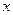 , відлік
, відлік 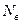 , стала
, стала 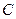 засобу вимірювань і ціна поділки шкали
засобу вимірювань і ціна поділки шкали 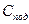 пов’язані між собою співвідношенням:
пов’язані між собою співвідношенням:
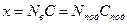 . (2.10)
. (2.10)
Одиниця молодшого розряду (ОМР) цифрового приладу — це розмір одного кванта 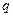 цифрового ЗВТ, що відповідає різниці між двома сусідніми станами цифрового вихідного значення. Поняття показу, відліку, сталої та ціни поділки, розглянуті стосовно аналогових ЗВ, поширюються і на цифрові ЗВ, для яких показ визначається співвідношенням
цифрового ЗВТ, що відповідає різниці між двома сусідніми станами цифрового вихідного значення. Поняття показу, відліку, сталої та ціни поділки, розглянуті стосовно аналогових ЗВ, поширюються і на цифрові ЗВ, для яких показ визначається співвідношенням
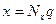 , (2.11)
, (2.11)
де 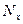 — кількість кроків квантування (квантів) з розміром
— кількість кроків квантування (квантів) з розміром 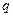 , який відповідає одиниці молодшого розряду (ОМР) цифрового ЗВ.
, який відповідає одиниці молодшого розряду (ОМР) цифрового ЗВ.
Із порівняння виразів (4.10) і (4.11) за їх структурою і змістом випливає, що для цифрового ЗВ стала збігається з ціною поділки і дорівнює розміру кроку квантування 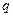 :
:
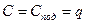 .
.
Вказані на шкалі найменше і найбільше значення величини 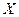 називають відповідно початковим
називають відповідно початковим 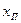 і кінцевим
і кінцевим 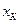 значеннями шкали ЗВ.
значеннями шкали ЗВ.
Інтервал значень шкали ЗВ, обмежений початковим і кінцевим її значеннями, називається діапазоном показів.
Та частина діапазону показів ЗВ, для якої пронормовані границі допустимих похибок, називається діапазонам вимірювань. Найменше і найбільше значення діапазону вимірювань називають нижньою 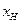 і верхньою
і верхньою 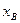 границею вимірювань.
границею вимірювань.
На рис. 1 зображена шкала вольтметра, в якого 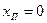 ,
, 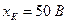 , а діапазон показів становить 0...50 В. Нижня границя вимірювання
, а діапазон показів становить 0...50 В. Нижня границя вимірювання 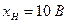 , верхня —
, верхня — 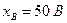 , а діапазон вимірювань становить
, а діапазон вимірювань становить 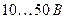 .
.
Верхня границя вимірювання 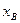 практично завжди збігається з верхньою границею показів ЗВ
практично завжди збігається з верхньою границею показів ЗВ 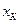 , тобто
, тобто 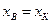 , а нижня границя вимірювання
, а нижня границя вимірювання 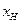 не завжди збігається з початковим значенням шкали ЗВ
не завжди збігається з початковим значенням шкали ЗВ 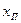 , як, зокрема, на рис. 4,9. Інтервал показів між позначками
, як, зокрема, на рис. 4,9. Інтервал показів між позначками  є неробочим і не входить в діапазон вимірювань ЗВ. У таких випадках нижню границю вимірювання ЗВ
є неробочим і не входить в діапазон вимірювань ЗВ. У таких випадках нижню границю вимірювання ЗВ 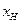 позначають на шкалі спеціальною точкою (див. рис. 4,9).
позначають на шкалі спеціальною точкою (див. рис. 4,9).
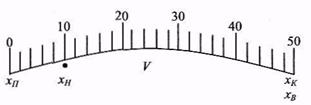
Рис.1.Шкала вольтметра
Задача 10.Визначити сталу вольтметра з границею вимірювання 75 В і максимальним відліком 150.
Розв’язання. Виходячи з того, що границя вимірювання вольтметра ( 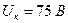 , а максимальний відлік
, а максимальний відлік 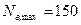 , за (2.9)
, за (2.9) 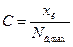 визначаємо сталу вольтметра:
визначаємо сталу вольтметра:
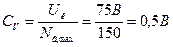
Взаємозв’язок між показом, відліком, сталою, і ціною поділки проаналізуємо на основі задачі 11 за рис. 2.
Задача 11.Задана шкала амперметра на 60 мА (див. рис. 2) і усталене положення вказівника (стрілки). Визначити відлік, кількість зчитаних поділок, сталу, ціну поділок та показ приладу 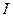 .
.
Разв’язання. 1. Проаналізувавши шкалу, встановлюємо, що границя вимірювання амперметра 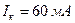 і максимальний відлік і максимальний відлік  , а максимальна кількість поділок , а максимальна кількість поділок 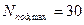 . 2. Враховуючи положення стрілки, встановлюємо, що . 2. Враховуючи положення стрілки, встановлюємо, що |  Рис.2.Шкала амперметра Рис.2.Шкала амперметра |
відлік 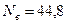 , а зчитана кількість поділок
, а зчитана кількість поділок 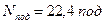 .
.
3. Із означення сталої 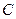 (2.9)
(2.9) 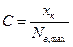 і ціни поділки
і ціни поділки 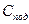 (2.8)
(2.8) 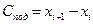 визначаємо: сталу амперметра
визначаємо: сталу амперметра
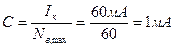
ціну поділки шкали
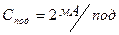
4. Показ приладу ІА відповідно до сталої (2.9) 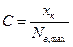 дорівнює
дорівнює
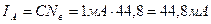
5. Показ приладу 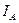 відповідно до ціни поділки (2.8)
відповідно до ціни поділки (2.8) 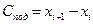 .дорівнює цьому самому значенню
.дорівнює цьому самому значенню
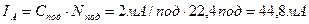
Практичне заняття №3
