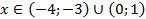Разработчик: И. А. Кочеткова

Цель работы:

1) Повторить определение логарифма.

2) Повторить теоремы логарифмирования, основное логарифмическое тождество, формулу перехода к новому основанию и следствия из нее.

3) Повторить основные методы решения показательных уравнений и неравенств.

4) Повторить основные методы решения логарифмических уравнений и неравенств.

Оборудование: карта индивидуального задания,

микрокалькулятор.

Порядок выполнения работы:

1. Изучить указания к выполнению практической работы.

2. Ответить на контрольные вопросы:

2.1. Что называется логарифмом некоторого числа b?

2.2. Какой логарифм называется десятичным? Натуральным?

2.3. Сформулировать и записать теоремы логарифмирования

2.4. Записать формулу перехода от логарифма по одному основанию к логарифму по другому основанию.

2.5. Записать следствия из формулы перехода к новому основанию.

2.6. Перечислите методы решения показательных уравнений

2.7. Перечислите методы решения логарифмических уравнений

2.8. Какая функция называется показательной? логарифмической?

2.9. Когда показательная и логарифмическая функции будут возрастающими, а когда убывающими?

2.10. Как решаются показательные и логарифмические неравенства?

3. Изучить условия заданий. Определить способ решения.

4. Решить примеры.

5. Оформить отчёт.

Указания к выполнению практической работы

Определение логарифма.

Логарифмом положительного числа b по положительному основанию 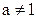называется такой показатель степени х, в который нужно возвести a, чтобы получить b:

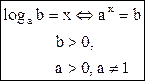
а)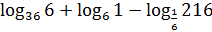

b)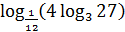

Решение.

a) Вычисляем каждый логарифм, используя определение:

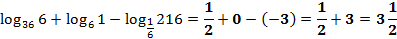
b) Вычисляем сначала внутренний логарифм, а затем логарифм от полученного числа

;

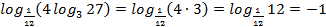Показательные уравнения

Пример 1.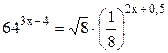

Решение. Приведём степени к одному основанию 8, для этого используем формулы 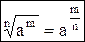и :

,

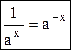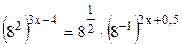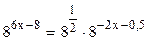; В правой части уравнения используем формулу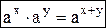

;

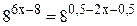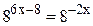
6x-8=-2x; 8x=8; x=1

Ответ. 1.

Пример 2.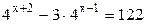

Решение. Применим формулы 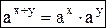и 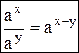, тогда уравнение примет вид:

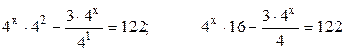
Вынесем неизвестную степень 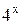за скобки и разделим уравнение на число, получившееся в скобках:

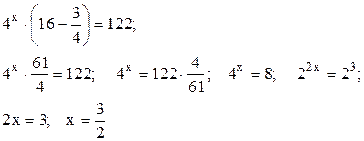
Ответ.

Пример 3. .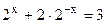

Решение. Перепишем уравнение в виде 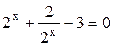и заменим 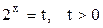, тогда уравнение примет вид:

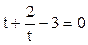. Умножим на t и получим квадратное уравнение:

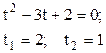
Значит 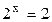или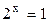

x=1 или x=0.

Ответ: 0; 1.

Пример.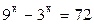

Решение. ; .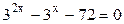

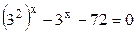Заменим 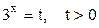, тогда уравнение примет вид:

.

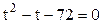Решаем квадратное уравнение и получаем: t₁= -8, t₂=9.

Т. к. t>0, то t₁= -8 не подходит.

Значит 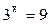, x=2

Ответ: х=2.

Показательные неравенства

Для решения показательных неравенств необходимо:

а) привести обе части неравенства к одному основанию, т. е. привести неравенство к виду:

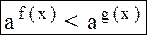, тогда

b) если a>1, то f(x)<g(x) (знак неравенства сохраняется);

если 0<a<1, то f(x)>g(x) (знак неравенства меняется на противоположный).

При решении неравенств можно пользоваться формулами:

1)	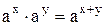3)	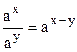5)	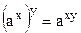7)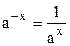
2)	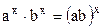4)	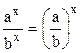6)	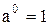8)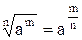

Пример 1.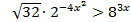

Используя свойства 8, 5 и 1, приведем неравенство к нужному виду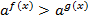

a)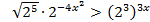

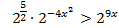
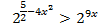
b) так как основание a=2>1, то показательная функция является возрастающей Þ знак неравенства сохраняется

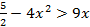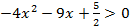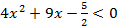; ;;умножим на 2 и получим

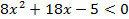
Получили квадратное уравнение, которое решим методом интервалов.

Найдем его нули: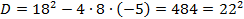

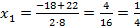
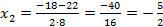
Разложим неравенство на линейные множители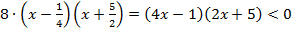

−

+

+

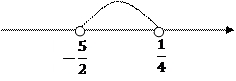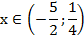
Нанесем точки на числовую прямую в порядке возрастания и определим знаки на каждом интервале:

x

Пример 2.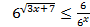

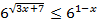
Т. к. основание a=6>1, то знак неравенства сохраняется

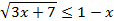
Получили иррациональное неравенство. Для его решения необходимо составить систему неравенств:

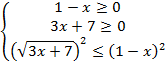
Решим каждое неравенство отдельно:

1. ; ; ;

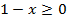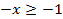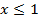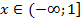
2. ; ; ;

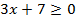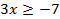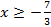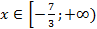
3. ;

;

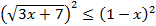
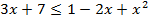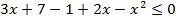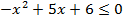
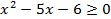
Нули: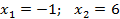

Разложим неравенство на линейные множители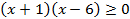

−

+

+

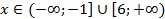
Нанесем точки на числовую прямую в порядке возрастания и определим знаки на каждом интервале:

x

Теперь определим общее решение системы: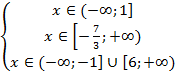

Найдем решение данной системы. Для этого нанесем решения неравенств на одну прямую:

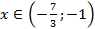
Логарифмические уравнения

1. log_af(x)=k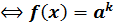

2. log_af(х) = log_ag(x)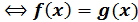

Для того, чтобы привести уравнение к виду (1) или (2), необходимо предварительно сделать подходящие преобразования логарифмов, входящих в уравнение. Такими преобразованиями могут быть:

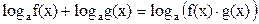
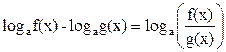
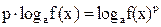
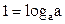, поэтому любое число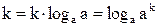

а так же переход от логарифма с одним основанием к логарифму с другим основанием:

, ,

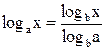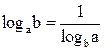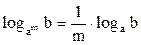
Пример . lg(x-3) + lg(x-2) = l – lg5

Решение.

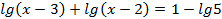
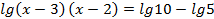
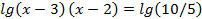
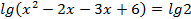
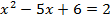
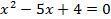
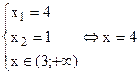
ОДЗ:

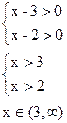
Ответ. 4

Логарифмические неравенства

Для решения логарифмических неравенств необходимо:

а) используя свойства логарифмов и известные приёмы решения логарифмических уравнений, привести неравенство к виду:

;

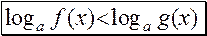b) составить основное неравенство, используя свойство:

если а>1, то f(x)<g(x) (знак неравенства сохраняется);

если 0<a<1, то f(x)>g(x) (знак неравенства меняется на противоположный);

c) к основному неравенству присоединить неравенства ОДЗ:

f(x)>0;

g(x)>0;

a>0;

a¹1

d) решить полученную систему неравенств.

Пример. 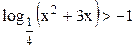Выполним все действия по алгорифму:

a) Приведем неравенство к нужному виду

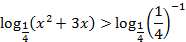
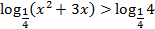
b) Так как основание 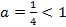, то логарифмическая функция является убывающей, значит знак неравенства нужно поменять на противоположный:

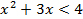
c) Добавим к данному неравенству неравенства ОДЗ (смотреть на условие примера)

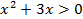
d) Итак, получим систему:

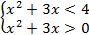
Решим отдельно каждое неравенство

1.

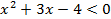
Нули: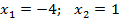

Разложим неравенство на линейные множители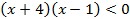

−

+

+

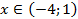
Нанесем точки на числовую прямую в порядке возрастания и определим знаки на каждом интервале:

x

2.

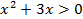
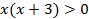
Нули: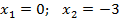

Разложим неравенство на линейные множители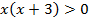

−

+

+

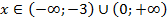
Нанесем точки на числовую прямую в порядке возрастания и определим знаки на каждом интервале:

x

3. Теперь определим общее решение системы:

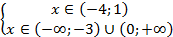
Найдем решение данной системы. Для этого нанесем решения неравенств на одну прямую: