Достаточные признаки сходимости знакопостоянных рядов
Признак сравнения.Пусть даны два ряда с положительными членами
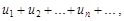 (6)
(6)
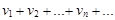 . (7)
. (7)
Если для всех n выполняется неравенство 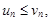 то из сходимости ряда (7) следует сходимость ряда (6), а из расходимости ряда (6) следует расходимость ряда (7).
то из сходимости ряда (7) следует сходимость ряда (6), а из расходимости ряда (6) следует расходимость ряда (7).
Замечание. При применении признака сравнения обычно в качестве эталонных рядов рассматриваются следующие ряды:
а) гармоничный ряд;
б) обобщенный гармонический ряд;
в) геометрический ряд.
Пример 6.Выяснить, сходится ли ряд 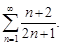
Решение
Так как 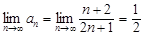 , т. е.
, т. е. 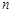 -й член ряда не стремится к нулю при
-й член ряда не стремится к нулю при 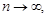 то ряд расходится.
то ряд расходится.
Тест 6. Для исследования вопроса сходимости ряда 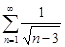 сравниваем его с
сравниваем его с 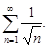 Делаем вывод:
Делаем вывод:
1) ряд расходится, так как 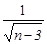 >
> 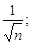
2) ряд сходится, так как 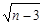 <
< 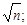
3) ряд сходится, так как 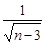 >
> 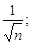
4) ряд расходится, так как 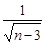 >
> 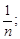
5) ряд расходится, так как 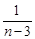 >
> 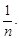
Предельный признак сравнения. Пусть даны два знакоположительных ряда
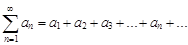 ,
,
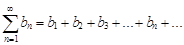
с неотрицательными членами, причем 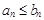 для всех n, начиная с некоторого.
для всех n, начиная с некоторого.
Тогда, если ряд 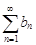 сходится, сходится и ряд
сходится, сходится и ряд 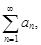 если же ряд
если же ряд 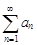 расходится, то расходится и ряд
расходится, то расходится и ряд 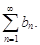
Пример 7.Исследовать сходимость ряда 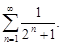
Решение
Члены ряда 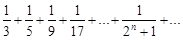 меньше соответствующих членов ряда
меньше соответствующих членов ряда 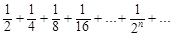 , который, являясь рядом бесконечно убывающей геометрической прогрессии, сходится. Следовательно, сходится и данный ряд.
, который, являясь рядом бесконечно убывающей геометрической прогрессии, сходится. Следовательно, сходится и данный ряд.
Тест 7. Чтобы исследовать ряд 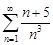 с помощью предельного признака сравнения, используем ряд
с помощью предельного признака сравнения, используем ряд  Находим:
Находим:
1) 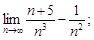
2) 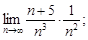
3) 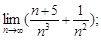
4) 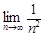 –
– 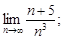
5) 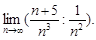
Признак Даламбера. Если существует предел 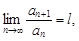 то ряд
то ряд 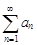 сходится при
сходится при 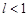 и расходится при
и расходится при 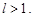
Замечание:
1. Если l = 1, то ряд может быть как сходящимся, так и расходящимся.
2. Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида n! или an.
Пример 8. Исследовать сходимость ряда
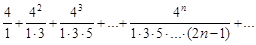 .
.
Решение
Воспользуемся признаком Даламбера. Общий член ряда 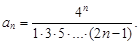 Поэтому
Поэтому 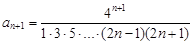 и
и 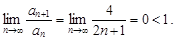 Ряд расходится. Заметим, что мы доказали также соотношение
Ряд расходится. Заметим, что мы доказали также соотношение 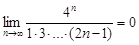 (общий член сходящегося ряда стремится к нулю).
(общий член сходящегося ряда стремится к нулю).
Тест 8. С помощью признака Даламбера определяем сходимость ряда 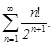 Тогда
Тогда 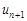 равен:
равен:
1) 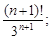
2) 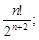
3) 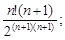
4) 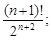
5) 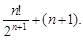
Признак Коши.Если существует предел
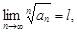 (8)
(8)
то ряд 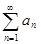 сходится при
сходится при 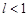 и расходится при
и расходится при 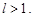
Замечание. Как и для признака Даламбера, в случае, когда l = 1, вопрос о сходимости ряда становится открытым.
Пример 9.Исследовать, сходится ли ряд 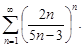
Решение
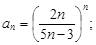
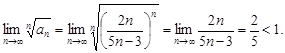 Ряд сходится.
Ряд сходится.
Тест 9.Чтобы исследовать ряд 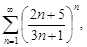 применяя признак Коши, необходимо найти:
применяя признак Коши, необходимо найти:
1) 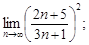
2) 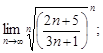
3) 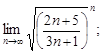
4) 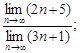
5) 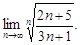
Пример 10.Исследовать сходимость ряда 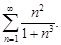
Решение
Применим интегральный признак Коши. По виду общего члена найдем функцию f(x)= 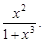
Вычислим несобственный интеграл
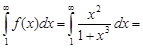
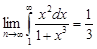
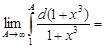
= 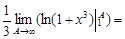
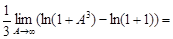
= 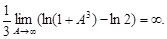
Интеграл расходится, следовательно, и ряд расходится.
Тест 10. Исследуем сходимость ряда 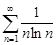 с помощью интегрального признака Коши. Найдем:
с помощью интегрального признака Коши. Найдем:
1) 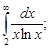
2) 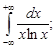
3) 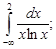
4) 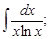
5)