Методика расчета кожухотрубного теплообменного аппарата
Тепловой расчет
Уравнение теплового баланса для теплообменного аппарата определяется по формуле 1.1:
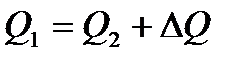 | (1.1) |
где 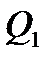 - количество теплоты в единицу времени, отданное греющим теплоносителем,
- количество теплоты в единицу времени, отданное греющим теплоносителем,
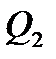 - количество теплоты в единицу времени, воспринятое нагреваемым теплоносителем,
- количество теплоты в единицу времени, воспринятое нагреваемым теплоносителем,
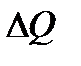 - потери теплоты в окружающую среду.
- потери теплоты в окружающую среду.
Так как по условию задания 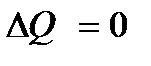 , то количество передаваемого тепла в единицу времени через поверхность нагрева аппарата, (Вт)определяется по формуле 1.2:
, то количество передаваемого тепла в единицу времени через поверхность нагрева аппарата, (Вт)определяется по формуле 1.2:
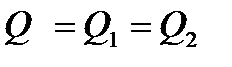 ;
;
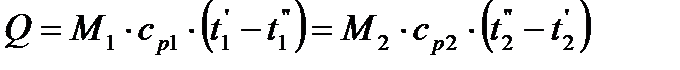 | (1.2) |
где 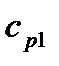 и
и 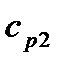 - средние удельные массовые теплоемкости греющего и нагреваемого теплоносителей, в интервале температур от
- средние удельные массовые теплоемкости греющего и нагреваемого теплоносителей, в интервале температур от 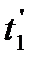 до
до 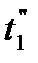 и от
и от 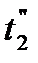 до
до 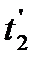 соответственно.
соответственно.
Температура нагреваемого теплоносителя на выходе из теплообменника определяется по формуле 1.3:
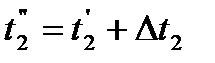 | (1.3) |
Средняя температура нагреваемого теплоносителя определяется по формуле 1.4:
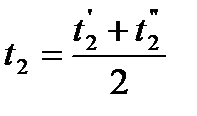 | (1.4) |
Средняя температура греющего теплоносителя определяется по формуле 1.5:
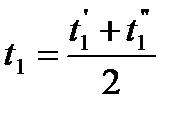 | (1.5) |
В первом приближении температура стенки определяется по формуле 1.6:
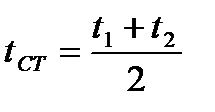 | (1.6) |
Среднюю скорость движения теплоносителя в трубах рекомендуется предварительно принимать в пределах 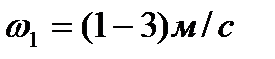 .
.
Критерий Рейнольдса для потока греющего теплоносителя определяется по формуле 1.7:
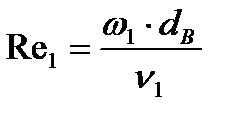 | (1.7) |
В результате сравнения вычисленного значения 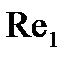 с критическим числом
с критическим числом 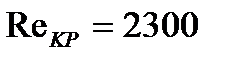 устанавливаем, что режим течения жидкости турбулентный и выбираем критериальное уравнение для расчета числа Нуссельта. Интенсивность теплоотдачи в круглых трубках зависит от режима движения теплоносителя.
устанавливаем, что режим течения жидкости турбулентный и выбираем критериальное уравнение для расчета числа Нуссельта. Интенсивность теплоотдачи в круглых трубках зависит от режима движения теплоносителя.
При турбулентном режиме течения жидкости ( 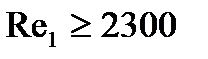 ) в круглых трубках и каналах число Нуссельта определяется по критериальной зависимости по формуле 1.8:
) в круглых трубках и каналах число Нуссельта определяется по критериальной зависимости по формуле 1.8:
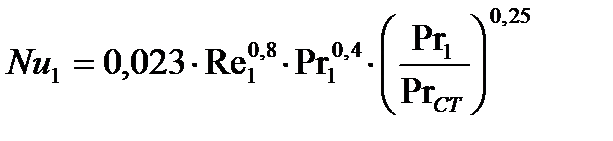 | (1.8) |
Определяющий размер – внутренний диаметр трубы, определяющая температура – средняя температура теплоносителя.
Коэффициент теплоотдачи от горячего теплоносителя к стенке трубы определяется по формуле 1.9:
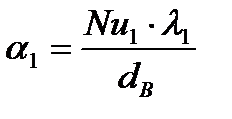 | (1.9) |
В результате сравнения вычисленного значения 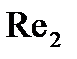 с критическим числом
с критическим числом 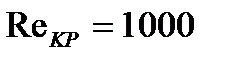 выбираем критериальное уравнение, по которому подсчитываем число Нуссельта. При движении теплоносителя в межтрубном пространстве коэффициент теплоотдачи рассчитывается по уравнению 1.10:
выбираем критериальное уравнение, по которому подсчитываем число Нуссельта. При движении теплоносителя в межтрубном пространстве коэффициент теплоотдачи рассчитывается по уравнению 1.10:
при 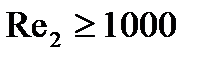
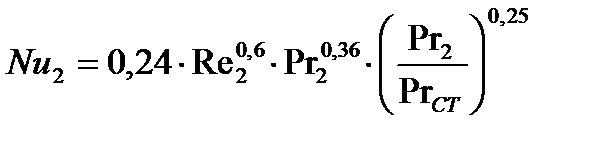 | (1.10) |
За определяющий геометрический размер принимают наружный диаметр теплообменных труб.
Коэффициент теплопередачи от стенок трубного пучка к нагреваемому теплоносителю определяется по формуле 1.11:
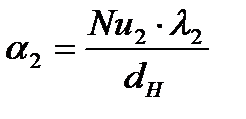 | (1.11) |
Если 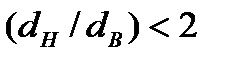 , то коэффициент теплопередачи для плоской поверхности теплообмена с достаточной точностью определяется по формуле 1.12:
, то коэффициент теплопередачи для плоской поверхности теплообмена с достаточной точностью определяется по формуле 1.12:
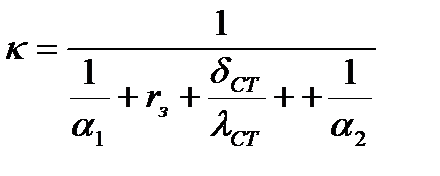 | (1.12) |
где 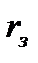 - термические сопротивления слоев загрязнений с обеих сторон стенки,
- термические сопротивления слоев загрязнений с обеих сторон стенки,
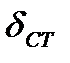 - толщина стенки,
- толщина стенки,
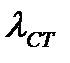 - коэффициент теплопроводности материала трубок.
- коэффициент теплопроводности материала трубок.
Вычислим среднелогарифмическую разность температур по формуле 1.13:
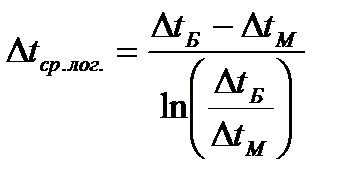 | (1.13) |
Из основного уравнения теплопередачи определяется необходимая поверхность теплообмена по формуле 1.14:
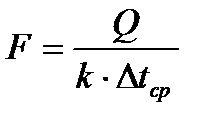 | (1.14) |
По рассчитанной площади и заданному диаметру труб выбирается стандартный теплообменный аппарат.
Гидравлический расчет
Полное гидравлическое сопротивление при движении жидкости в трубах теплообменного аппарата определяется выражением 1.15:
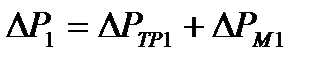 | (1.15) |
где 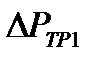 - гидравлическое сопротивление трения.
- гидравлическое сопротивление трения.
Гидравлическое сопротивление трения определяется по формуле 1.16:
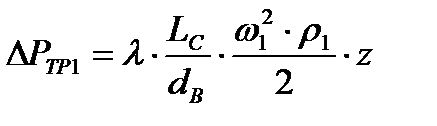 (1.16)
(1.16)
где 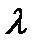 - коэффициент трения,
- коэффициент трения,
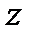 - число ходов теплоносителя по трубному пространству
- число ходов теплоносителя по трубному пространству
Потери давления, обусловленные наличием местных сопротивлений определяются по формуле 1.17:
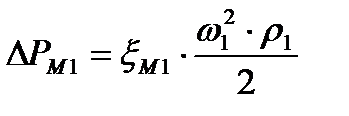 (1.17)
(1.17)
где 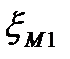 - сумма коэффициентов местных сопротивлений трубного пространства определяется по формуле 1.18:
- сумма коэффициентов местных сопротивлений трубного пространства определяется по формуле 1.18:
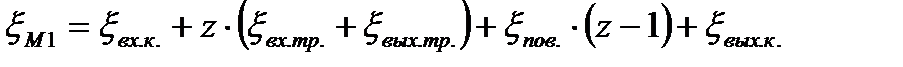 (1.18)
(1.18)
где 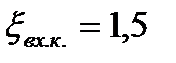 и
и 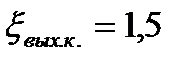 - коэффициенты сопротивлений входной и выходной камер.
- коэффициенты сопротивлений входной и выходной камер.
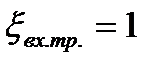 и
и 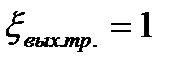 - коэффициенты сопротивлений входа в трубы и выхода из них.
- коэффициенты сопротивлений входа в трубы и выхода из них.
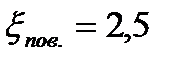 - коэффициент сопротивления поворота между ходами.
- коэффициент сопротивления поворота между ходами.
Целевая функция (З) представляет собой функцию затрат, включающую в себя капитальные затраты (Зкап) и эксплуатационные затраты (Зэкспл).
Выразив все зависимости через переменные w и dвн, представленные в вышеописанной методике, следующую формулу:
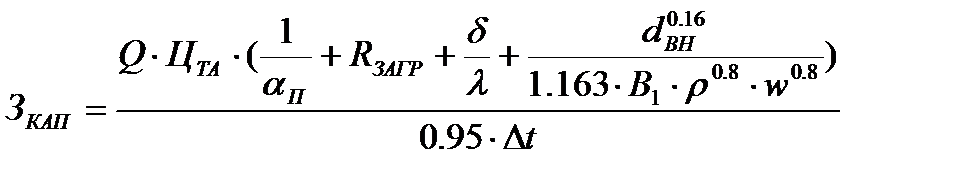
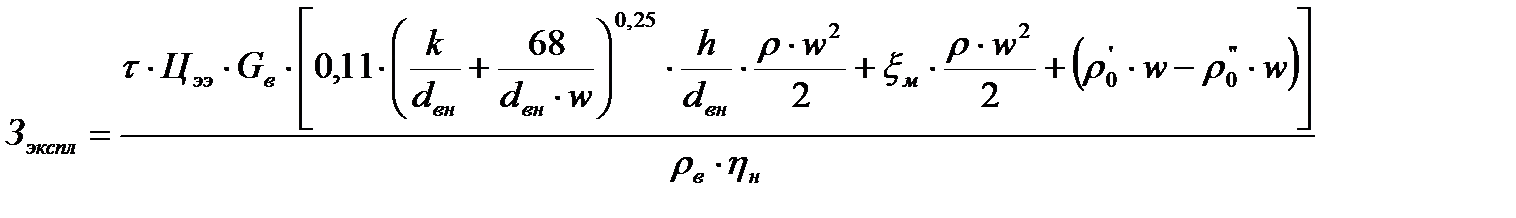
В итоге целевая функция для оптимизации теплообменного аппарата принимает следующий вид 1.19:
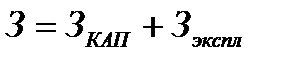 (1.19)
(1.19)
Метод Ньютона
В основе метода Ньютона лежит квадратичная аппроксимация целевой функции. Последовательность итераций строится таким образом, чтобы во вновь получаемой точке градиент аппроксимирующей функции обращался в нуль.
Последовательность приближений строится в соответствии с формулой 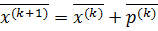 ,
,
где 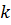 — номер итерации (
— номер итерации ( 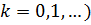 ,
,
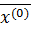 — начальное приближение,
— начальное приближение,
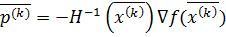 — вектор направления спуска.
— вектор направления спуска.
Здесь 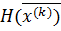 — матрица Гессе.
— матрица Гессе.
Направление спуска 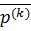 ведет к убыванию целевой функции только при положительной определенности матрицы Гессе
ведет к убыванию целевой функции только при положительной определенности матрицы Гессе 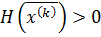 . В тех итерациях, в которыхматрица Гессе отрицательно определена
. В тех итерациях, в которыхматрица Гессе отрицательно определена 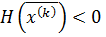 ,последовательность приближений к точке минимума строится по методу наискорейшего градиентного спуска. С этой целью проводится замена вектора направления спуска на антиградиентное
,последовательность приближений к точке минимума строится по методу наискорейшего градиентного спуска. С этой целью проводится замена вектора направления спуска на антиградиентное 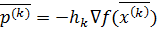 .
.
