Правила записи приближенных чисел
Пусть приближенное число 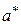 задано в виде конечной десятичной дроби:
задано в виде конечной десятичной дроби:
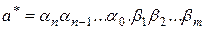 , (2.6)
, (2.6)
т.е.
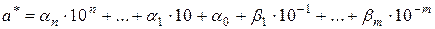 . (2.7)
. (2.7)
Значащими цифрами числа 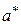 называют все цифры в его записи, начиная с первой ненулевой слева ([3], стр. 28).
называют все цифры в его записи, начиная с первой ненулевой слева ([3], стр. 28).
Например, у чисел 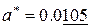 и
и 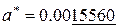 значащими являются подчеркнутые цифры.
значащими являются подчеркнутые цифры.
Значащая цифра приближенного числа 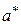 называется верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре ([3], стр. 29).
называется верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре ([3], стр. 29).
Например, если 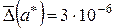 , то у числа
, то у числа 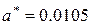 все значащие цифры – верные, а у числа
все значащие цифры – верные, а у числа 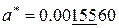 имеет три верные значащие цифры.
имеет три верные значащие цифры.
Широко распространенной ошибкой при записи приближенных чисел является отбрасывание последних значащих нулей (даже если они представляют верные цифры).
Количество верных значащих цифр тесно связано со значением его относительной погрешности. Известны следующие результаты.
Теорема ([3], стр. 29)
1. Если число 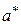 содержит N значащих цифр, то справедливо неравенство:
содержит N значащих цифр, то справедливо неравенство:
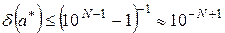 . (2.8)
. (2.8)
2. Для того чтобы число 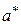 содержало N верных значащих цифр, достаточно чтобы выполнялось неравенство:
содержало N верных значащих цифр, достаточно чтобы выполнялось неравенство:
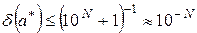 . (2.9)
. (2.9)
3. Если число 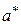 имеет ровно N значащих цифр, то
имеет ровно N значащих цифр, то
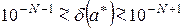 , (2.10)
, (2.10)
т.е.
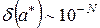 . (2.11)
. (2.11)
Здесь знак 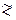 означает знак приближенного неравенства, а ~ - знак эквивалентности.
означает знак приближенного неравенства, а ~ - знак эквивалентности.
Границы абсолютной и относительной погрешностей принято записывать с одной или двумя значащими цифрами. Большая точность в записи этих величин, как правило, не имеет смысла, так как обычно они являются довольно грубыми оценками истинных значений погрешностей, и кроме того, для практического использования часто бывает достаточно знать их порядок ([3], стр. 30).
Например, информация о погрешности вида 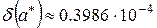 практически равноценна информации
практически равноценна информации 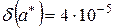 , причем последняя больше вызывает доверия. Вполне удовлетворительной в этом случае будет и запись
, причем последняя больше вызывает доверия. Вполне удовлетворительной в этом случае будет и запись 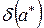 ~10 -5.
~10 -5.
Из неравенства (2.4) следует, что истинное значение а удовлетворяет двойному неравенству:
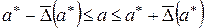 . (2.12)
. (2.12)
Факт, что число 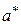 является приближенным значением числа а с верхней границей абсолютной погрешности
является приближенным значением числа а с верхней границей абсолютной погрешности 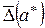 (с абсолютной точностью
(с абсолютной точностью 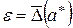 ) принято записывать в виде ([3], стр. 30):
) принято записывать в виде ([3], стр. 30):
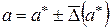 . (2.13)
. (2.13)
При этом, как правило, числа 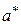 и
и 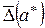 указывают с одинаковым числом цифр после десятичной точки.
указывают с одинаковым числом цифр после десятичной точки.
Из неравенства (2.5) следует, что значение а заключено приблизительно между 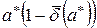 и
и 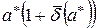 (проверить самостоятельно), поэтому факт, что число
(проверить самостоятельно), поэтому факт, что число 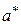 является приближенным значением числа а с границей относительной погрешности
является приближенным значением числа а с границей относительной погрешности 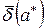 (с относительной точностью
(с относительной точностью 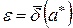 принято записывать в виде ([3], стр. 30):
принято записывать в виде ([3], стр. 30):
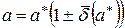 . (2.14)
. (2.14)
Если число 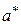 приводится в качестве результата без указания погрешности, то принято считать, что все его значащие цифры являются верными ([3], стр. 31).
приводится в качестве результата без указания погрешности, то принято считать, что все его значащие цифры являются верными ([3], стр. 31).
Начинающий пользователь часто слишком доверяет выводимым из компьютера цифрам, предполагая, что вычислительная машина придерживается того же соглашения. Однако это совсем не так: число может быть выведено с таким количеством значащих цифр, сколько потребует программист заданием соответствующего формата. Как правило, среди этих цифр только небольшое число первых цифр окажутся верными, а возможно верных цифр нет совсем. Анализировать результаты вычислений и определять степень их достоверности совсем непросто. Одна из целей вычислительных методов и состоит в достижении понимания того, что можно и чего нельзя ожидать от результатов, полученных на компьютере ([3], стр. 31).
Округление
Часто возникает необходимость в округлении числа а, т.е. в замене его другим числом 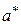 с меньшим числом значащих цифр. Возникающую при такой замене погрешность называют погрешностью округления.
с меньшим числом значащих цифр. Возникающую при такой замене погрешность называют погрешностью округления.
Существует несколько способов округления числа до n значащих цифр.
Наиболее простой – усечение, который состоит в отбрасывании всех цифр, расположенных справа от n- ой значащей цифры ([3], стр. 31).
Абсолютная погрешность округления усечением не превышает единицы разряда, соответствующего последней оставляемой цифре.
Более предпочтительным является округление по дополнению. В простейшем варианте это округление состоит в следующем ([3], стр. 31): если первая слева из отбрасываемых цифр меньше 5, то сохраняемые цифры остаются без изменения. Если же она больше или равна пяти, то в младший сохраняемый разряд добавляется единица.
Абсолютная погрешность округления при округлении по дополнению не превышает половине единицы разряда, соответствующего последней оставляемой цифре.
Границы абсолютной и относительной погрешностей принято всегда округлять в сторону увеличения ([3], стр. 31).
