Метод конечных элементов
Метод конечных элементов изначально разрабатывался для прочностных расчетов. Там он и сейчас является самым массовым методом. Позже отдельные его разновидности получили широкое распространение и в других областях. Здесь рассмотрим формулировку Галеркина, получившую наибольшее распространение (по крайней мере за пределами прочностностных задач).
В рассматриваемой формулировке метод конечных элементов можно рассматривать как частный случай метода Галеркина. От классического варианта метода Галеркина его отличает, главным образом, то, что в качестве пробных используются непрерывные финитные функции, т.е. функции равные нулю везде, кроме конечной области. Кроме того, каждая из этих функций в некоторой узловой точке равна единице, а в остальных узловых точках она равна нулю. Здесь возникает еще одно отличие от классической формулировки метода Галеркина: коэффициенты в разложении искомой функции приобретают конкретный физический смысл – это значения этой самой функции в узлах. Итак, функция ищется в виде
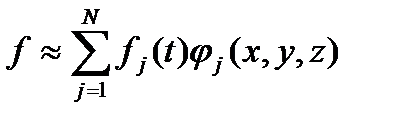
где fj(t) – приближенные значения искомой функции в узлах, а jj(x,y,z) – пробные функции. Пробные функции (называемые также интерполяционнымии или функциями формы), как правило, выбираются из числа кусочно-линейных (или полилинейных).
Рассмотрим сначала одномерный случай. Кусочно-линейные пробные функции при этом будут иметь вид:
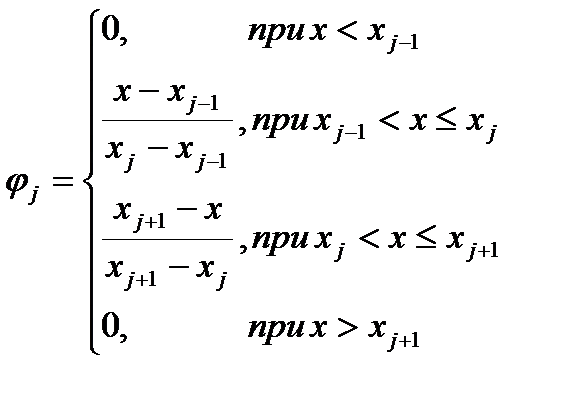
Представим эти функции графически, получаем
| Xi |
| Xi-1 |
| Xi-2 |
| Xi+1 |
| Xi+2 |
| jj |
| jj-1 |
| jj+1 |
Очевидно, что при таком выборе пробных функций целевая функция будет между узлами интерполироваться линейно. Гораздо реже можно встретить вариант с квадратичной интерполяцией. При этом «четные» и «нечетные» пробные функции будут записываться по-разному. Не буду записывать формулы (желающие могут написать их самостоятельно), приведу рисунок.
| Xi |
| Xi-1 |
| Xi-2 |
| Xi+1 |
| Xi+2 |
| jj |
| jj-1 |
| jj+1 |
Использование квадратичной интерполяции повышает порядок аппроксимации получаемого решения, но заметно усложняет процесс нахождения его нахождения (особенно для двумерных и трехмерных случаев).
Рассмотрим двумерный случай. Наложим на расчетную область треугольную или прямоугольную сетку. Каждая пробная функция будет задана на ячейках, содержащих какой-то узел сетки. Тогда для каждого конечного элемента (области, где пробная функция отлична от нуля) легко записать пробную функцию. В центральном узле она равна единице, а на периферии нулю. В каждой из ячеек мы можем написать линейную или билинейную функцию, которая будет удовлетворять этим условиям. Так для треугольной области напишем
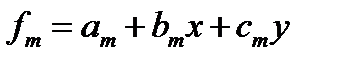
а для прямоугольной
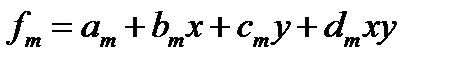
Для трехмерного случая принцип построения пробных функций точно такой же.
Научившись выписывать пробные функции можно выписать систему уравнений, которую предстоит решать. Как и в классическом методе Галеркина это будут уравнения вида
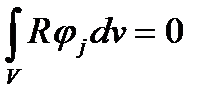
Так как использовались финитные пробные функции, то каждое из этих уравнений будет содержать лишь ограниченное число неизвестных.
Рассмотрим теперь применение на конкретном примере. Прежде, чем рассмотрим применение метода конечных элементов, решим задачу, которая нам еще не раз понадобится.
Задача: в направлении оси X идет пучок частиц первого вида. Все частицы имеют одинаковую скорость. Эти частицы могут сталкиваться с частицами второго вида, при этом частицы первого вида переходят в некоторое другое состояние или превращаются в другие частицы (например, вследствие ионизации, рекомбинации, возбуждения или чего-нибудь еще). Скорость частиц первого вида считаем неизменной. Вопрос: как меняется вдоль оси X концентрация частиц первого вида в начальном состоянии?
Чтобы получить ответ нужно решить в одномерной постановке уравнение сохранения массы.
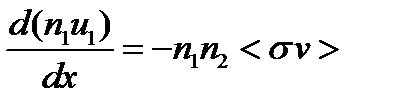
где величина <sv> характеризует интенсивность взаимодействия частиц разных видов. В силу неизменности скорости первых частиц получаем простое дифференциальное уравнение относительно концентрации
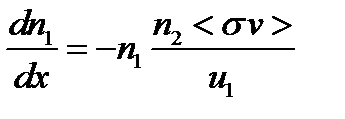
Такое уравнение легко решается аналитически
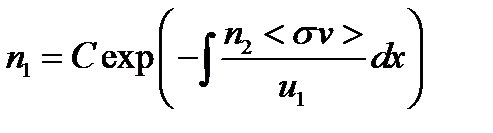
а в случае, когда подынтегральное выражение является константой, то еще проще
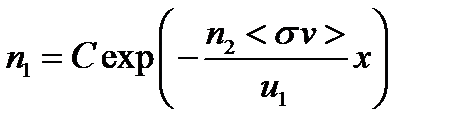
константа находится из граничных условий.
Другой вариант этой же задачи: какова вероятность того, что частица первого вида пролетит расстояние L без каких-либо изменений? Совершенно аналогичным образом получаем ответ (если подынтегральное выражение – константа)
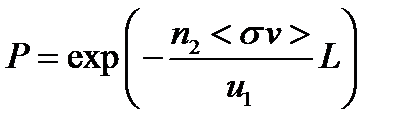
Теперь возвращаемся к методу конечных элементов. Рассмотрим решение дифференциального уравнения
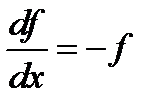
на отрезке [0,1] с граничным условием f(0)=1. Пример реального уравнения такого типа мы только что рассмотрели. Рассмотрим случай с тремя узлами в точках 0, 0.5 и 1. Значение в одном из них задано граничным условием. С учетом этого аппроксимацию функции можно записать следующим образом
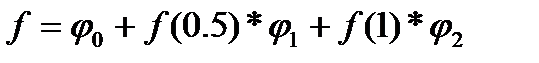
при этом имеем следующие определения для пробных функций.
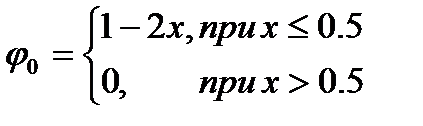
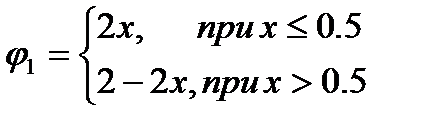
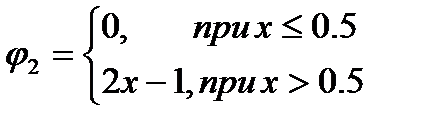
Невязку исходного уравнения можно записать в виде
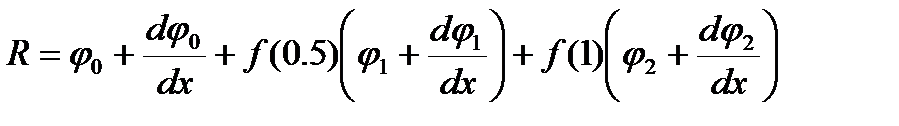
Уравнения, которые предстоит решить, выглядят так
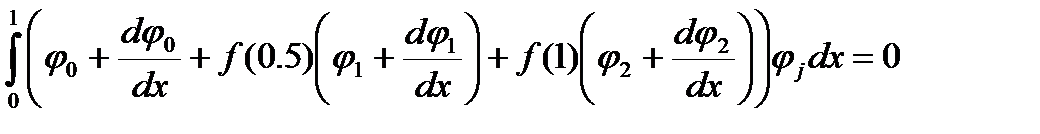
Здесь начинаются преимущества финитных функций, особенно при равных шагах между узлами. Произведение функций, чей индекс отличается более чем на единицу, равно нулю. Это же справедливо и для произведения производной на функцию. Интегралы от ненулевых произведений (при равных шагах между узлами) одинаковы для случаев с одинаковыми разностями индексов. Все эти интегралы можно посчитать один раз и потом всю жизнь пользоваться. Для данного случая (одномерная задача с равномерным шагом) это выглядит так
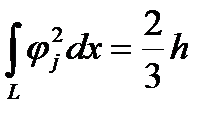
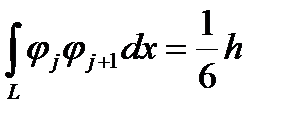
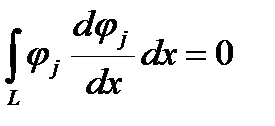
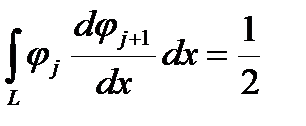
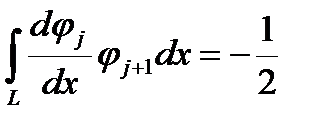
Нужно учесть, что в крайних узлах могут быть отличия. Если поставлено какое-то граничное условие, то из него и получается уравнение для данного узла. Если граничного условия нет, то нужно помнить, что в крайнем узле интегрирование произведения функции самой на себя или свою производную берется по вдвое меньшему интегралу. Поэтому получаем
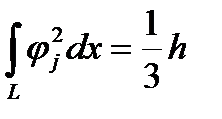
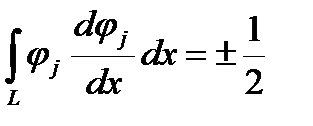
В последнем случае знак положителен на правом конце и отрицателен на левом. Теперь спокойно получаем систему уравнений
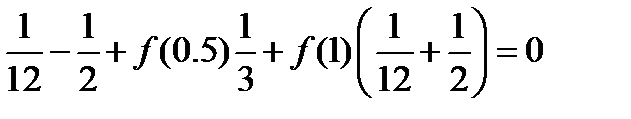
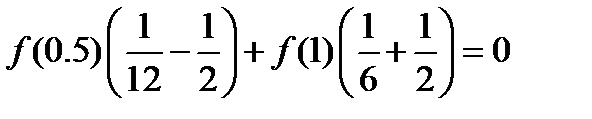
после упрощений окончательно получаем
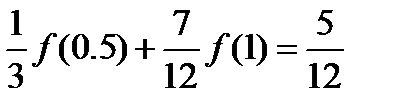
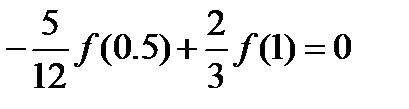
решая эту систему получаем
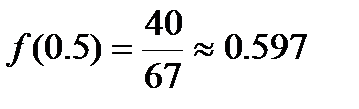
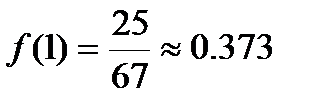
Аналитическое решение того же уравнения дает f(0.5)»0.607 и f(1)=0.368.
Зная интегралы от произведений пробных функций, можно рассмотреть общий случай. Так для уравнения вида
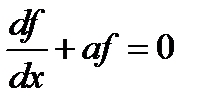
для центральных узлов (не граничных) получаем уравнения вида
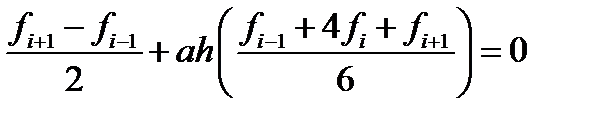
По сути дела, это тоже разностная схема, только умноженная на шаг. Следовательно, ее можно анализировать теми же методами, какие применяются для метода конечных разностей.
Это все замечательно, но возникает вопрос: как быть, если в исходное уравнение входят вторые производные, а в методе конечных элементов используются линейные аппроксимации? Оказывается, выход есть. Нужно применить один интересный прием. Продемонстрируем его на примере уравнения Пуассона
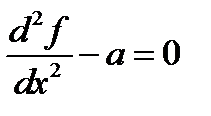
Невязкой такого уравнения будет
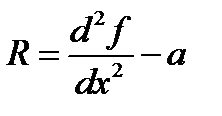
Следовательно, задача сводится к решению уравнений вида
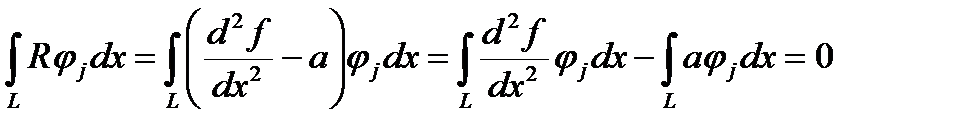
А теперь для первого интеграла применим интегрирование по частям, получим
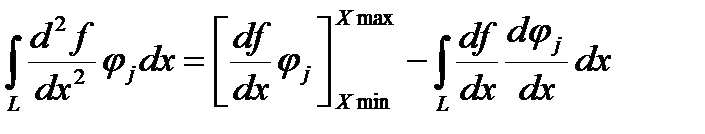
Первый член в этом соотношении для большинства функций fj равен нулю. Исключение составляют функции равные единице в граничных точках, но там существуют граничные условия, избавляющие нас от необходимости нахождения этого члена. Таким образом, для внутренних узлов необходимо решать уравнения вида
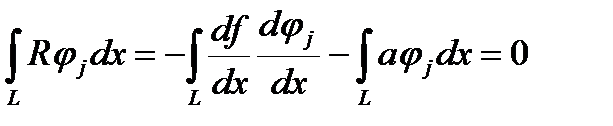
Теперь можно вспомнить, что
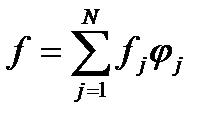
и уравнения преобразуются к виду
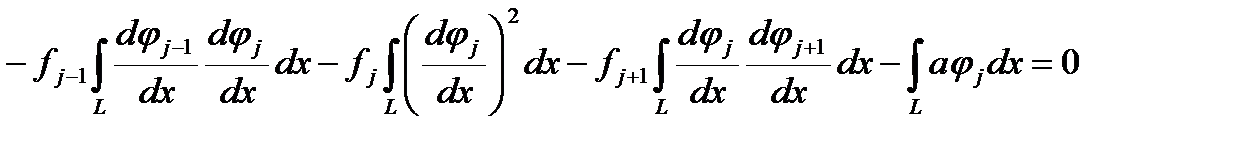
интегралы от пробных функций известны. Для линейной интерполяции с равномерным шагом они выглядят так (для центральных узлов)
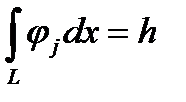
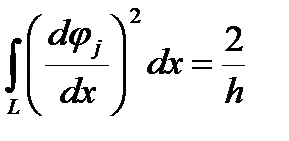
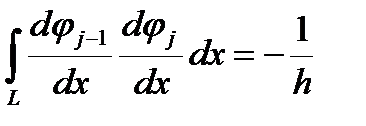
Таким образом, получаем уравнения, которые предстоит решить
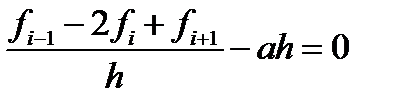
Мы получили (с точностью до постоянного множителя) разностную схему, аналогичную получаемой из метода конечных разностей.
Лекция 6. Информационная. Дается понятие о статистической модели. Излагается метод статистических испытаний. Рассказываются общие принципы построения и исследования статистических моделей. Приводятся примеры статистических моделей элементов двигателей летательных аппаратов. Основы теории массового обслуживания.
Ранее мы рассматривали детерминированные модели. То есть такие, в которых конечный результат однозначно определяется исходными данными. На практике часто приходится сталкиваться с влиянием случайных факторов. Например, на нынешнем уровне развития техники трудно представить себе двигатель, который проработает до первого отказа точно заданный срок (ни на 1% больше, ни на 1% меньше). И причин тому много: микродефекты материалов, погрешности обработки, неточности при сборке, различия в условиях эксплуатации и т.п. Все это тоже нужно как-то моделировать.
Для моделирования объектов с большим влиянием случайных факторов широко применяется метод статистических испытаний или метод Монте-Карло. Суть его сводится к многократному повторению расчетов с целью получения статистически значимых результатов.
Простейший вариант применения статистического моделирования состоит в многократном использовании детерминированной модели с различными исходными данными. Таким образом мы сможем выявить влияние случайных отклонений (и самое главное их комбинаций) на выходные характеристики исследуемого объекта. Конечно, в линейных моделях это не актуально, ибо связь между входными и выходными параметрами часто можно получить аналитическими методами. Но в технике часто приходится иметь дело с нелинейными задачами, где зависимости бывают не столь очевидными. Например, возьмем межконтинентальную баллистическую ракету, которую в норме двигатель должен разгонять до скорости 7.5 км/с. Если двигатель придаст ей чуть меньший импульс и разгонит лишь до 7 км/с, то это приведет к резкому сокращению дальности полета. А если двигатель придаст больший импульс и разгонит до 8 км/с, то ракета может выйти на орбиту и летать неопределенно долго. Таким образом, простейшими линейными методами достоверно предсказать результат моделирования не получится, и часто легче произвести серию расчетов с различными исходными данными.
Однако, часто варьирование исходных данных оказывается недостаточным, так как велико влияние случайных факторов внутри самого рассматриваемого объекта. Такая ситуация типична для моделирования разреженных сред. Это характерно для электроракетных двигателей. Там случайные факторы существенно влияют на взаимодействие частиц друг с другом и со стенкой. Конечно, даже в разреженной среде частиц настолько много, что особенности одного соударения никак не влияет на конечный результат. Следовательно, можно создать детерминированную модель для расчета таких процессов. И такие модели есть, например, уравнение Больцмана. Однако, расчеты по таким моделям оказываются настолько громоздкими, что обычно гораздо проще провести расчет методом Монте-Карло.
Приведу несколько примеров расчетов. Первый – расчет потоков ионов в ускорительной системе ионного двигателя. В районе ускоряющего электрода формируется так называемый мениск – выгнутая поверхность, по которой проходит граница квазинейтральной плазмы. В расчетах ускорительной системы можно принять, что ионы стартуют с этой поверхности и далее ускоряются электрическим полем. Однако в силу ряда причин в каждой точке мениска стартовые скорости неодинаковы как по на модулю, так и по направлению. В силу этого некоторые ионы могут попадать на ускоряющий электрод, что приводит к его постепенному разрушению. Моделирование подобных процессов приходится проводить методом Монте-Карло. Задается закон распределения стартовых скоростей и рассчитываются траектории большого количества частиц.
E 3siurftBcIx2ed2DDownD34Y8+RCnwU3BPgTFbS4i8p5Ivw5jedgm0nUv0QFie6iJj6dR+ITub7q W7kmytfaTEI675wf1qpGgqObrTOT7cD1Q/jZmtH3nLKQ0AjGirE0DFPK/TARV88z2fWM+WL6rnJ4 L+ZizDHjNDwx3KvSVu4hqE/j+I4Jb1VXUm0q+8/la2VX7cfe7KSDYFfExo7OhTc+6mhMNPH/LtcZ /jD+VTRWngKjAEQgHkeIC29GZySZRaGHI0wEjNiLh6yXkBCFHmGwoV6MKOFeSCIiYGYk8jgRJPE4 YoQNaUYAi8whKKjHGGJQTt/8F3dvePTFbwAAAP//AwBQSwECLQAUAAYACAAAACEAmzMnNwwBAAAt AgAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4 /SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAD0BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAL qeT4ugEAAE8DAAAOAAAAAAAAAAAAAAAAADwCAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAA IQB5GLydvwAAACEBAAAZAAAAAAAAAAAAAAAAACIEAABkcnMvX3JlbHMvZTJvRG9jLnhtbC5yZWxz UEsBAi0AFAAGAAgAAAAhAICkFUTdAAAACAEAAA8AAAAAAAAAAAAAAAAAGAUAAGRycy9kb3ducmV2 LnhtbFBLAQItABQABgAIAAAAIQAfV+3VDQIAANsEAAAQAAAAAAAAAAAAAAAAACIGAABkcnMvaW5r L2luazEueG1sUEsFBgAAAAAGAAYAeAEAAF0IAAAAAA== ">
Картинка
Другой пример – пылезащитные устройства двигателей. Тут тоже приходится рассчитывать большое количество траекторий частиц (в данном случае пыли). Но главным образом сказывается не различие в начальной скорости, а различие в массе и размерах пылинок.
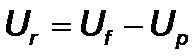
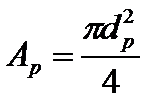
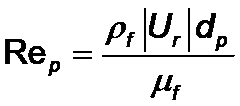
Наконец еще один пример. Расчет движения твердых частиц в сопле ЖРД. При сгорании топлива остается некоторое количество мелких твердых частиц (например, сажа). В сопле эти частицы ускоряются потоком до очень больших скоростей. Поэтому их столкновение с поверхностью приводит к постепенному ее разрушению, что может повлиять на ресурс конструкции. Естественно, стараются выбрать такую геометрию сопла, чтобы минимизировать подобные негативные явления.
Теперь совсем коротко о точности расчетов методом Монте-Карло. В большинстве случаев отдельные испытания (например, частицы в приведенных выше примерах) можно считать независимыми. Тогда погрешность конечного результата обратно пропорциональна корню из числа испытаний. То есть если мы хотим удвоить точность, нужно вчетверо увеличить объем расчетов. Это приводит к тому, что обычно приходится проводить очень большое число испытаний. Часто специалисты на расчеты с числом частиц менее ста тысяч даже не реагируют, считая их несерьезными. В настоящее время типичным являются числа частиц от миллиона и более.
При изложении статистических методов необходимо упомянуть пару математических теорий. Естественно здесь я изложу лишь самые простые их задачи и результаты. Первая теория носит название случайного блуждания. Среди прочего в ней рассматривается задача пошагового перемещения точи по оси. На каждом шаге точка сдвигается на случайную величину. Для простоты обычно ограничиваются случаем симметричного распределения вероятности перемещения. То есть сдвиги влево и вправо равновероятны. Если результаты предыдущих движений никак не влияют на новое, то через некоторое число шагов плотность вероятности положения точки будет распределена по близкому к нормальному закону (следствие центральной предельной теоремы). Но гораздо более важен другой факт: дисперсия этого распределения будет пропорциональна корню из числа шагов. А если шаги взаимозависимы? Тогда степень в этом распределении будет иной, да и нормальность распределения не гарантируется. В частности, если более вероятно движение в направлении предыдущего шага, то показатель степени будет больше. В физике результаты этой теории часто используются для описания процессов диффузии, теплопередачи и вязкости.
Другая интересная теория называется теорией массового обслуживания. Не следует упрощенно понимать ее название. Эта теория рассматривает реакцию некой системы на поступающие в нее сигналы. В частности с ее помощью рассчитываются задачи типа перехвата воздушных целей. Применительно к двигателям можно рассматривать вопрос о реакции двигателя на поступающие команды (например, маневрирование во время боя или захода на посадку). Сама теория рассматривает некую абстрактную систему в которую в случайные моменты времени поступают некие сигналы. На обработку каждого сигнала система тратит некоторое время. Если за это время придет еще один сигнал, то ему придется «постоять в очереди» на обработку. Часто вводят еще один параметр: максимальное время, которое сигнал может ждать в очереди. В частности, если обозначить через р отношение среднего времени обслуживания к среднему времени между сигналами, то длину очереди можно оценить по формуле
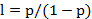
Отсюда видно, что если параметр стремиться к единице, то длина очереди стремиться к бесконечности. В жизни справедливость этого вывода можно ощутить на себе в различных учреждениях, где как раз и исходят из предположения, что время обслуживания должно быть равно среднему времени между приходом клиентов. А применительно к двигателям эта теория указывает нам на жесткие требования к приемистости авиационных двигателей.
Модели хищник-жерва, эпидемия
Практические и семинарские занятия– 4 часа.
Занятие 1. Линейные детерменированные модели. Нелинейные детерминированные модели. Форма проведения занятий – дискуссия. Отрабатываемые вопросы: классификация математических моделей и выбор подхода к решению поставленной задачи.
Занятие 2.Статистические модели элементов двигателей летательных аппаратов. Форма проведения занятий – решение задач. Отрабатываемые вопросы: расчет параметров отдельных элементов конструкции двигателей летательных аппаратов.
Статистические модели и метод статистического моделирования. Принципы преимущества и недостатки статистических моделей по сравнению с детерминированными моделями. Основные законы распределения случайных величин и их использование. Точность статистического моделирования.
Статистическое моделирование физических полей (метод случайных блужданий по сетке). Задание граничных условий. Точность метода и число реализаций. Параметры решения задач с помощью случайных блужданий.
Оценка точности результатов статистического моделирования.
Связь погрешности результатов статистического моделирования с числом проеденных реализаций.
Лабораторный практикум – 4 часа, 1работа.
Статистическое моделирование. Цель работы: знакомство с влиянием случайных факторов на интегральные характеристики элементов двигателей летательных аппаратов. Форма выполнения в группах по 10 чел. Работа проводится в терминальном классе.
Управление самостоятельной работой студента9 часов:
проработка материалов лекций – 4 часа; подготовка к практическим занятиям и анализ результатов полученных в ходе их проведения – 5 часов.
Раздел 3. Аналоговые модели и аналоговое моделирование элементов ДЛА
Теоретические занятия (лекции) – 2 часа.
Лекция 1. Информационная. Рассказывается об аналоговых моделях и аналоговом моделировании элементов двигателей летательных аппаратов. Излагаются общие принципы моделирования полей. Рассматриваются аналоговые модели стационарных полей и нестационарных полей. Приводятся примеры моделирования физических полей в элементах двигателей летательных аппаратов.
Что такое индикатор аналогии? Роль индикатора аналогии при создании аналоговых моделей.
Принципы аналогового моделирования. Аналогичные явления и объекты. Физические поля как объект аналогового моделирования. Математическое описание стационарных и нестационарных физических полей. Основные уравнения и краевые условия. Аналогия физических полей различной природы.
Масштабы аналогии и выбор масштабов аналогии.
Вывод инидикатора аналогии и его смысл. Масштабы аналогии и их выбор. Количество индикаторов аналогии и пи-теорема Кирпичева. Различные варианты записи индикатора аналогии. Преобразование граничных условий при аналоговом моделировании.
Аналоговые модели на основе сплошных проводящих сред. Проводящие среды. Задание формы модели. Плоскопараллельные области и области с осевой симметрией. Задание граничных условий. Изменение распределения потенциала.
Аналоговые модели на основе сеток электрических сопротивлений. Принципы построения моделей. Сравнительный анализ аналоговых моделей на основе сплошных сред и сеток сопротивлений. Моделирование нестационарных физических полей (общие принципы и подходы).
Аналоговое моделирование с использованием не электрических моделей. Общие принципы и подходы. Гидротепловая аналогия Лукьянова и возможности ее использования при аналоговом моделировании физических полей с фазовыми переходами.
Греческое слово аналогия обозначает сходство или соответствие. Человечество с древних времен использовало замену одного объекта другим со сходными свойствами для решения различных задач. Чаще всего для упрощения. Хотя порой и для сознательного введения в заблуждение. Можно даже заявлять, что авиация возникла из-за желания человека летать аналогично птицам. Однако оставим лингвистические и философские аспекты этого слова и займемся использованием аналогии в технике, особенно в моделировании.
В сложной технике аналоги используются очень широко. Например, для тестирования отдельных элементов дорогих систем используются имитаторы отдельных подсистем. У военных это дешевые мишени вместо реальных объектов. Часто встречаются встроенные системы самоконтроля и самотестированя. В самом простейшем случае это выглядит как «контроль ламп» - для проверки просто включаются цепи питания индикации имитируемых событий. Отдельные случаи реализовывать не просто дорого, но еще и опасно. Прежде всего это относится к аварийным ситуациям. Естественно для проверки различных систем в таких условиях применяются различные способы имитации. Однако в приведенных примерах аналогии применяются не в целях расчета. Математическое моделирование здесь применяется в лучшем случае лишь на этапе создания имитаторов.
При разработке техники также широко применяются подобные модели. Самый простой вариант – подобие по размерам. Уменьшенные копии летательных аппаратов продуваются в аэродинамических трубах, копии судов испытываются в бассейнах. Математические методы тут используются для пересчета результатов таких испытаний на натуральный размер объекта.
Более интересные варианты бывают при замене одной среды на другую с целью удешевления или облегчения эксперимента. Например, замена воздуха на воду. Или замена охлажденных до криогенных температур компонентов топлива или окислителя на другую жидкость при более близких к комнатной температурах (как вариант – на ту же воду). Используемый математический аппарат при этом несколько усложняется, но не сильно. Хоть среда и заменяется, но она относится к тому же классу, лишь с другими значениями отдельных параметров.
Но под аналоговыми методами обычно понимают моделирование, основанное на принципиально иных физических принципах, чем исследуемый объект. Такое становится возможным потому, что часто различные физические процессы описываются одинаковыми уравнениями. На этом пути человечество придумало великое множество разнообразных способов. Приведу несколько примеров.
Гидротепловая аналогия. Наиболее медленными процессами в технике обычно являются тепловые. Для ускорения испытаний их можно заменить какими-нибудь более быстрыми. Один из вариантов – гидротепловая аналогия. Вместо источников тепла ставим источники жидкости, вместо тепловых сопротивлений используем гидравлические, вместо температуры измеряем давление. Простейший примера такой модели представлен на рисунке.
Рис. Со стр. 118 Чуяна
Но наиболее удобными оказались разнообразные электрические аналогии. Они позволяют измерять напряжение и ток. А комбинации различных сопротивлений, конденсаторов и катушек позволяли моделировать разнообразные взаимосвязи между отдельными элементами. Так с помощью накопления заряда в конденсаторе можно решать задачу интегрирования, а с помощью индуктивности моделировать дифференцирование. С появлением же компактной полупроводниковой техники стали использовать и более сложные готовые блоки, например операционные усилители. Даже простейшие диоды уже позволяли моделировать сложные нелинейные связи между элементами. Создавались специальные аналого-вычислительные машины (АВМ), представляющие собой набор из стандартных элементов с возможностью легкой внешней коммутации в разнообразные схемы. С помощью таких машин можно было решать, например, разнообразные алгебраические, дифференциальные и даже интегральные уравнения и системы уравнений.
Однако с таким подходом хорошо решать обыкновенные дифференциальные уравнения или системы с очень небольшим числом параметров. А на практике часто нужно найти распределения физических величин (скорости, плотности, температуры, напряжения) в пространстве. Для этого нужны уже другие подходы. Естественным образом возникает идея моделировать одни физические поля другими. Проще всего оказалось проделывать такое с помощью электролитических ванн и проводящей бумаги. При этом мы можем измерять электрический потенциал. Соответственно можно моделировать либо скалярные поля (например температуру), либо потенциалы векторных полей (например скорости). Научились даже моделировать неравномерные значения коэффициентов в уравнениях варьируя толщину бумаги. Однако, фактически можно анализировать лишь те явления, которые сводятся к уравнениям Лапласа или Пуассона. Таковых конечно много, но далеко не все задачи относятся к этому классу. Пришлось искать другие подходы.
По аналогии с сеточными численными методами стали делать сетки из сопротивлений. Такой подход был очень громоздким, зато давал возможность моделировать практически любые системы. В настоящее время в связи с развитием вычислительной техники этот способ аналогового моделирования практически вышел из употребления.
