Дослідження перехідних процесів

В ЕЛЕКТРИЧНИХ КОЛАХ ДРУГОГО ПОРЯДКУ

Мета роботи– вивчити перехідні процеси в лінійному нерозгалуженому колі RLC при підключенні його до джерела постійної та синусоїдальної напруги. Зняти осцилограми напруг і струмів при перехідних процесах на реактивних елементах контуру.

Теоретичні відомості

Припустимо, що перемикач на схемі рис. 8.1 перемикається з лівого положення в праве, причому до комутації конденсатор зарядився до величини напруги джерела .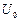

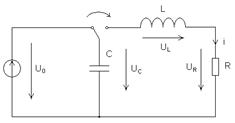
Рис. 8.1. Схема нерозгалуженого кола RLC

Після комутації для послідовного контуру RLC на основі другого закону Кірхгофа для миттєвих значень можна записати, що

,

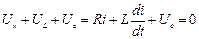так як 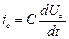, то

,

то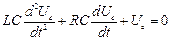бто одержане лінійне диференціальне однорідне рівняння другого порядку для напруги на ємності 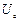, характеристичне рівняння якої

.

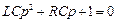Загальне рішення однорідного диференціального рівняння складається тільки з вільної складової

,

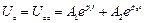де 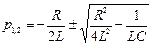– корені характеристичного рівняння.

Залежно від відношення параметрів корені можуть бути дійсними різними (якщо 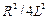> 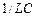чи 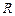> 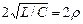), дійсними рівними ( 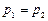якщо 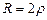) і комплексними спряженими (якщо < )

.

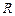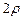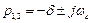У першому та другому випадках процес в колі – аперіодичний, в послідовному – коливальний, причому 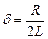– коефіцієнт згасання; 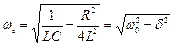– частота вільних коливань; – частота власних коливань; 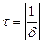– стала часу коливального контуру.

Підставивши комплексні значення коренів одержимо залежність від часу при коливальному процесі напруги на ємнісному елементі, а потім і для розрядного струму:

;

.

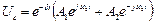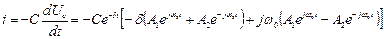Для знаходження сталих інтегрування 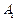і 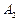звернемося до законів комутації для індуктивного та ємнісного елементів. До комутації в момент часу 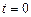– напруга на ємнісному елементі дорівнювала напрузі джерела живлення 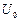, а струму в індуктивному елементі не було. Тоді можемо записати, що

;

.

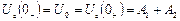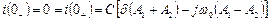Звідси

; .

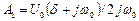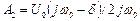Враховуючи, що за формулою Ейлера 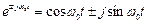, тоді отримаємо залежність напруги на ємнісному елементі від часу у вигляді

.

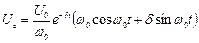Суму косинусоїдальної і синусоїдальної функцій можна замінити однією синусоїдальною функцією. Для цього припустимо, що відношення 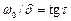, тому будемо вважати, що 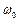і 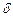– катети прямокутного трикутника, гіпотенуза якого дорівнює .

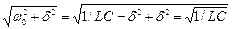Тоді отримаємо

,

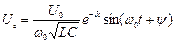а струм

.

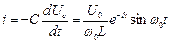Останні залежності показують, що напруга ємнісного елемента і розрядний струм можна розглядати, як синусоїдально змінні в часі величини, але з амплітудами, які зменшуються за експоненціальним законом при сталій часу 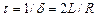. Залежності 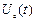і розрядного струму подані на рис. 8.2.

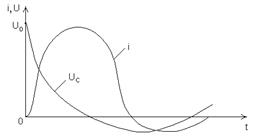
Рис. 8.2. Залежності напруги на ємнісному елементі та розрядного

струму від часу при коливальному процесі в колі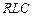

Якщо 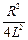> 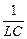, то дійсні корені характеристичного рівняння мають негативні різні значення, причому 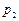< <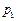0. Для знаходження сталих 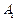і 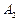скористуємося також законами комутації для ємнісного та індуктивного елементів:

;

,

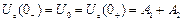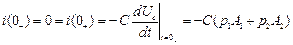тобто

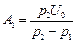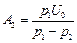>0; <0.

Підставив значення сталих інтегрування, одержимо напругу на ємнісному елементі:

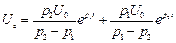
та значення струму розрядки:

.

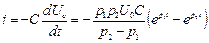Криві зміни напруги приведені на рис. 8.3.

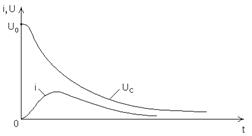
Рис. 8.3. Залежності напруги на ємнісному елементі та розрядного

струму від часу при аперіодичному процесі розрядки в колі

Для граничного випадку аперіодичного процесу при 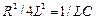характеристичне рівняння має два однакових дійсних корені 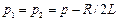(кратні корені). При кратних коренях загальне рішення диференціального рівняння записується як 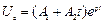, де стал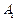і і 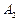визначаються на основі законів комутації. Тоді напруга на ємнісному елементі і струм за час граничного аперіодичного процесу розряду:

; .

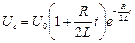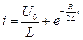При увімкненні нерозгалуженого кола 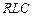до напруги вільна складова перехідного процесу накладається на примусову складову. Коли коло вмикається до постійної напруги 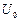(рис. 8.4), то 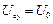і 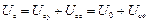, причому для аперіодичного випадку 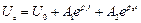, для коливального .

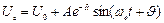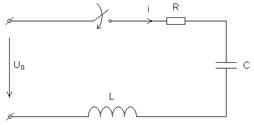
Рис. 8.4. Увімкнення кола 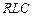до напруги джерела живлення

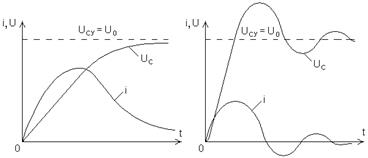
На рис. 8.5 а та б зображені графіки зміни напруги на конденсаторі і струму в колі для аперіодичного і коливального процесів.

а б

Рис. 8.5. Залежності напруги на ємнісному елементі та струму в колі при аперіодичному (а); та коливальному процесі (б)

Коли аперіодичний контур вмикається до синусоїдальної напруги 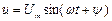, то загальне рішення для напруги на конденсаторі буде мати такий вигляд:

;

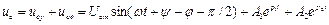згасаюча аперіодична крива вільної складової накладається на встановлену синусоїдальну складову і графік виглядає так, ніби крива вільного процесу стала криволінійною віссю синусоїдальних коливань. У міру згасання вільного процесу криволінійна вісь коливань переходить у вісь абсцис.

При увімкненні коливального контуру до синусоїдальної напруги відбувається накладання гармонічного встановленого процесу і вільного процесу згасаючих коливань.

Тоді напруга на конденсаторі запишеться як

.

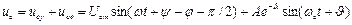Вигляд кривої такого процесу залежить від співвідношення частот вільних коливань 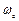та змушених коливань 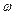, які задаються джерелом живлення. Коливання меншої частоти стають криволінійною віссю для другого коливання. Коли частоти 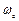і 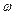достатньо близькі одна до одної, то виникає специфічний процес коливань.

При увімкненні контуру до синусоїдальної напруги, то перехідний процес залежить від моменту ввімкнення.

Порядок виконання роботи

1. Накреслити електричну схему нерозгалуженого кола
(рис. 8.1).

2. Параметри електричного кола 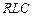вибрати відповідно до варіанта з табл. 8.1.

Таблиця 8.1

Пара-метри	Варіанти
Е, В
R, Ом
L, мГн
C, мкФ

3. Скласти диференціальні рівняння відносно струму в колі та напруги на конденсаторі:

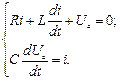
4. Визначити коефіцієнт згасання 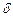, частоту вільних коливань 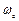, частоту власних коливань 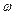, сталу часу 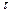коливального контуру, визначити час практичного існування перехідного процесу .

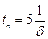5. Провести розрахунок диференціальних рівнянь за допомогою програмного пакета Mathcad 2000.

6. Здійснити математичне моделювання нерозгалуженого електричного кола. Зняти осцилограми перехідних струмів та напруг на реактивних елементах. Порівняти результати моделювання та розрахунків.

7. Накреслити схему нерозгалуженого електричного кола
(рис. 8.4), яке підключається до джерела постійної напруги.

8. Скласти диференціальні рівняння відносно струму та напруги на конденсаторі і визначити початкові умови:

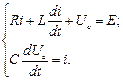
Провести розрахунок диференціальних рівнянь.

9. Побудувати графіки перехідного струму та перехідних напруг на реактивних елементах.

10. Здійснити математичне моделювання електричного кола 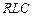. Зняти осцилограми перехідних струмів та напруг на реактивних елементах і порівняти їх з результатами розрахунків.

11. Накреслити схему нерозгалуженого електричного кола 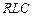(рис. 8.4), яке підключається до джерела синусоїдальної напруги.

12. Параметри електричного кола вибрати відповідно до варіанта з табл. 8.2.

13. Визначити власну частоту коливального контура 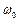, різницю частот 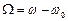, період коливань 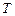джерела напруги.

Таблиця 8.2

Пара-метри	Варіанти
Е, В
R, Ом
L, мГн
C, мкФ
F, Гц

14. Скласти диференціальні рівняння стану коливального контура та провести їх розрахунок:

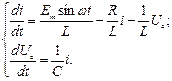
15. Побудувати графіки перехідного струму та напруг на реактивних елементах.

16. Здійснити математичне моделювання електричного кола з джерелом напруги синусоїдальної форми. Зняти осцилограми перехідних струмів та напруг на реактивних елементах. Порівняти результати моделювання та розрахунки.

Зміст звіту

Звіт повинен містити:

1. Мету і порядок виконання роботи;

2. Схеми досліджуваних електричних кіл другого порядку;

3. Диференціальні рівняння перехідних процесів та їх розрахунок;

4. Графічні залежності перехідних струмів і напруг на реактивних елементах за результатами розрахунку диференціальних рівнянь;

5. Осцилограми перехідних струмів та напруг на елементах досліджених електричних кіл;

6. Порівняння результатів розрахунку перехідних процесів з результатами математичного моделювання;

7. Короткі висновки за результатами роботи.

Контрольні питання

1. З яких складових складається загальне рішення неоднорідного диференціального рівняння?

2. Як визначаються сталі інтегрування?

3. Назвіть типи перехідних процесів залежно від відношення параметрів 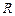, , 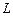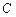елементів схеми.

4. Як визначається час практичного існування перехідного процесу?

Лабораторна робота 9