Показательный закон распределения

Биноминальный закон.

Биноминальный закон распределения характеризует вероятность появления события А n раз в m независимых испытаниях. Если вероятность появления события А в одном опыте равна r (соответственно вероятность его не появления равна 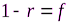), а число независимых испытаний равно m, то вероятность появления события А n раз в серии m испытаний 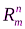может быть представлена математической формулой биноминального закона распределения следующим образом

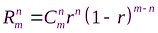
где 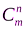- число сочетаний m по n, равное .

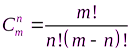Биноминальным закон распределения назван потому, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона. Биноминальный закон распределения применяется при статическом контроле при ограниченной информации о свойствах приборов, которые необходимо расклассифицировать на годные и дефектные.

Закон Пуассона.

Распределение по закону Пуассона обычно применяется для определения вероятности появления заданного числа независимых и несовместимых событий на заданном интервале времени. Вероятность возникновения события А не менее n раз в интервале времени 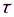по закону Пуассона задается выражением

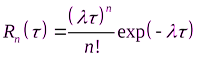
где 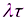- положительный параметр 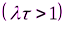, представляющий собой среднее число отсчетов за рассматриваемый интервал времени, а n – обычная факториальная целочисленная функция.

Распределение Пуассона является предельным случаем биноминального распределения при неограниченном возрастании числа испытаний.

Гипергеометрический закон.

Пусть в партии изделий объемом N имеется F дефектных. Если взять из всей этой партии методом случайного отбора выборку объемом n, то вероятность того, что во взятой нами выборке окажется f дефектных изделий, в общем случае описывается гипергеометрическим законом

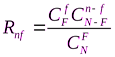
Равномерный закон распределения

Определение. Распределение вероятностей непрерывной случайной величины Х на интервале [a, b] называется равномерным, если плотность вероятности f(х) постоянна на этом интервале и равна нулю вне него ,т.е.:

f(х) = C = const, если хÎ[a, b],

f(х) = 0, если хÏ[a, b].

Плотность вероятности обладает следующим свойством: 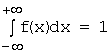. Подставляя, получим:

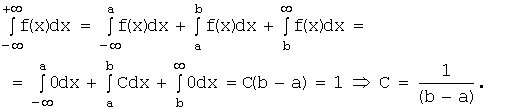Откуда:

.

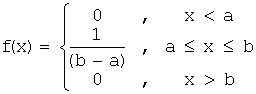Функция распределения F(X) может быть найдена путем интегрирования плотности вероятности: .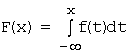

Таким образом: .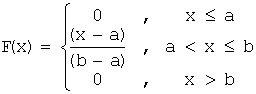

Математическое ожидание: ,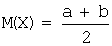

дисперсия: .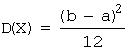

Показательный закон распределения

Определение. Показательный(экспоненциальный) закон распределения непрерывной случайной величины Х задается плотностью вероятности:

.

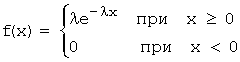Функция распределения: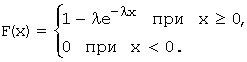

Математическое ожидание: ;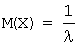

дисперсия: ;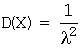

среднее квадратическое отклонение: .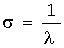

Характерная особенность этого распределения – равенство математического ожидания среднему квадратическому отклонению.

Нормальный закон распределения(закон Гаусса)

Определение. Нормальный закон распределения (закон Гаусса) непрерывной случайной величины Х задается плотностью вероятности :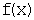

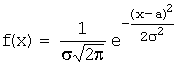,где:

а и s - параметры распределения, которые равны, соответственно, ее математическому ожиданию и среднему квадратическому отклонению, т.е. М(Х)= = а, дисперсия .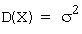

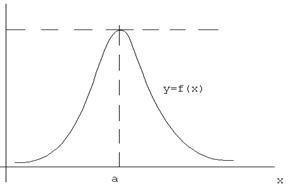
График плотности нормального распределения 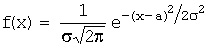представляет собой кривую симметричную относительно прямой x=a с ординатой, максимальной в точке x=a, и равной 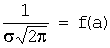. Этот график называется кривой Гаусса.

Функция распределения имеет вид:

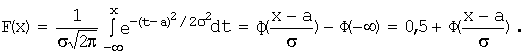Вероятность попадания случайной величины в интервал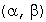 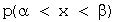записывается в виде: 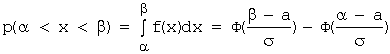, где Ф(x)-функция Лапласа.

Распределение Пирсона χ² (хи-квадрат)

Карл Пирсон (Pearson, 1857-1936) английский математик и биолог. С целью проверки теории Дарвина разработал статистический метод, получивший широкое распространение при исчислении коэффициента корреляции между различными переменными. В частности, в 1900 г. им предложен критерий ‘хи-квадрат’. В литературе часто упоминается осуществленный Пирсоном опыт по экспериментальной проверке вероятности выпадания герба при подбрасывании монеты. Из 24000 подбрасываний, герб выпал 12012 раз.

Определение. Распределением χ² (хи квадрат) с n степенями свободы называется распределение суммы квадратов n независимых случайных величин, каждая из которых распределена по нормальному закону с параметрами M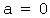X= и DX= 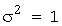, т.е: ,

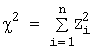где: Z_i (i =1,2, …,n) - набор n независимых, нормально распределенных случайных величин.

Плотность вероятности распределения χ² определяется выражением:

,

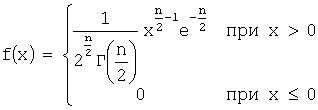где: 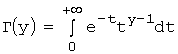- гамма-функция Эйлера (можно показать, что для целых положительных значений аргумента гамма-функция Эйлера принимает более простой вид: ).

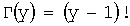Распределение Стьюдента

Уильям Госсет (1876-1937) – английский статистик, писавший под псевдонимиом “Student” (стьюдент).

Определение. Распределением Стьюдента (или 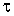-распределением) называется распределение случайной величины ,

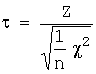где: Z - случайная величина, распределенная по нормальному закону с параметрами M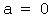X= и DX= 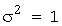, χ² – независимая от Z случайная величина, имеющая распределение χ² с n степенями свободы.

Критерий Фишера

Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону.

F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий:

причем в числителе ставится большая из двух дисперсий. Расчетное F сравнивают с _____________, которое находятиз таблиц, для степеней свободы _____________________________________где N₁ - число элементов выборки, по который вычислена_______ .

N₂ - число элементов выборки, по которым получена оценка дисперсии ________.

Если F < F _кр , то принимается нулевая гипотеза о равенстве генеральных дисперсий _________________ при принятом уровне значимости q .

На рис. 1.3 показаны кривые распределения _____. Зачернена об­ласть критических значений F .

На практике задача сравнения дисперсий возникает, если требуется сравнить .точность приборов, инструментовили методов измерений. Предпочтительнее тот прибор, инструмент или метод, который обеспечи­вает наименьшее рассеяние результатов измерений, т.е. наименьшую дис­персию.