К проведению практического занятия по математике

Методические указания № 13

для студентов 2-го курса медико-биологического факультета

(отделение медицинская биохимия)

в 3-м семестре 2015-2016 уч. г.

ТЕМА: «ЭЛЕМЕНТЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА: ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ»

Цель: формировать понятия: статистическая связь; корреляционная связь; направление связи, сила (теснота) связи, форма связи, линеаризация уравнений

Задача 1. В результате эксперимента получена зависимость аккомодации глаза ( 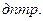) от возраста (в годах):

Возраст
Аккомодация				8,5	7,0	5,5	4,5

Требуется:

1) построить корреляционное поле и сформулировать гипотезу о форме связи.

2) предполагая, что данная зависимость между X и Y близка к линейной, найти выборочный коэффициент корреляции ;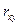

3) проверить достоверность найденного значения выборочного коэффициента корреляции при уровне значимости ;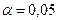

4) найти уравнения линейной регрессии Y на X

5) оценить качество модели, вычислив индекс детерминации

6) построить линию регрессии на графике экспериментальных данных.

7) Найти прогнозное значение признака Y, если X_p = 45 лет

Решение

1) Построим корреляционное поле данных

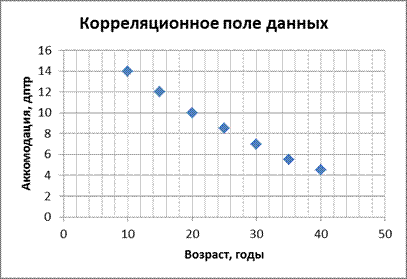
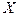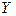Анализ корреляционного поля данных показывает, что между признаками и в выборочной совокупности существует обратная (отрицательная) и достаточно тесная линейная связь.

2) Вычислим выборочный коэффициент парной корреляции

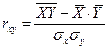Для вычисления средних значений признаков и их среднеквадратических отклонений составим расчётную таблицу:

№	x, годы	y, дптр	x*y	x^2	y^2
		8,5	212,5		72,25
		5,5	192,5		30,25
		4,5			20,25
Σ(Суммы)		61,5			611,75
средние		8,79	187,86	725,00	87,39

На основании полученных данных находим:

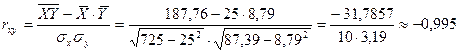ВЫВОД: в ВЫБОРОЧНОЙ СОВОКУПНОСТИ между признакам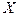и и 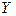обнаружена очень тесная отрицательная (или обратная) связь

3) 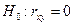проверим достоверность найденного значения выборочного коэффициента парной корреляции при уровне значимости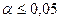

Проверяется нулевая гипотеза

на уровне значимости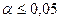

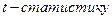Для проверки гипотезы используем

Вычислим наблюдаемое значение критерия:

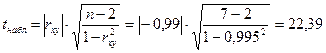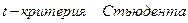Найдем табличное значение

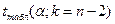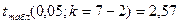ВЫВОД. Нулевая гипотеза отвергается на уровне значимости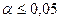

То есть коэффициент корреляции существенно отличается от нуля. Иначе, и в генеральной совокупности между аналогичными признаками существует очень сильная отрицательная связь.

4) Построим уравнение регрессии вида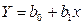

Параметры уравнения регрессии найдем из системы уравнений, полученной МНК

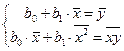
Подставим в систему найденные значения средних:

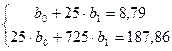
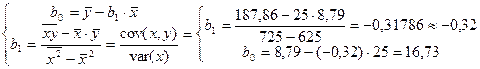Далее находим параметры уравнения регрессии:

Уравнение регрессии имеет вид: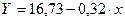

Параметр 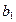или выборочный коэффициент регрессии 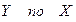показывает, что при увеличении переменной 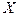– возраста человека – на 1 год переменная 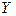(аккомодация глаза) в среднем снижается на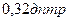

5) Оценим качество модели, вычислив индекс детерминации

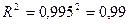
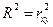Так как в случае ПАРНОЙ РЕГРЕССИИ индекс детерминации совпадает с квадратом коэффициента корреляции , то для построенной модели индекс детерминации будет равен:

ВЫВОД: аккомодация 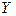почти на 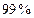зависит от 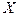(возраста человека), а 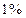вариации 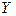происходит под влиянием других, неучтенных в модели факторов.

В парной линейной регрессиипроверки значимости

коэффициента регрессии,

коэффициента корреляции

и коэффициента (индекса) детерминации эквивалентны.

Статистическая значимость коэффициента корреляции установлена.

Поэтому можно утверждать, что и найденной уравнение регрессии статистически значимо и его можно использовать для прогноза

6) Найдём прогнозное значение признака Y, если X₂ = 45 лет

Прогноз: при Xp =45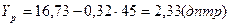

7) Для построения ЛИНИИ регрессии достаточно двух точек:

x, годы	Y,теор
	13,6
	4,0

Yтеор вычислили, подставив значения Х в уравнение регрессии.

Нанесём координаты этих точек на корреляционное поле данных и соединим прямой линией

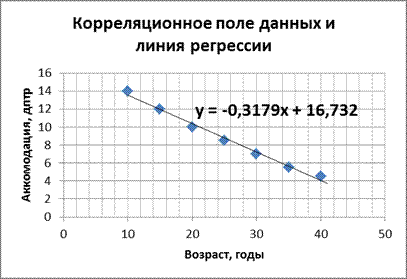
Задача 2 (шутка). Имеются данные о зависимости между ежегодным потреблением бананов 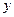и годовым доходом 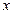10 американских семей (усл. ед.):

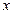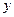Постройте уравнение регрессии вида 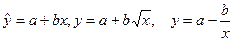. Выберите наилучшую модель.

Решение.

1. Построим корреляционное поле данных.

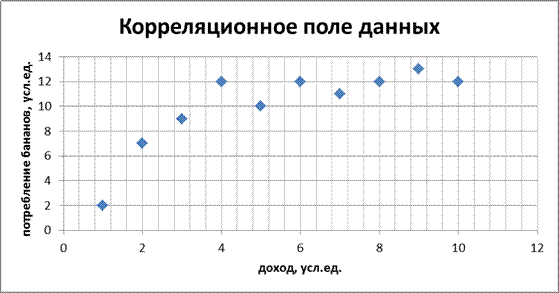
Анализ корреляционного поля данных показывает, что между признакам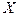и и 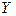в выборочной совокупности существует прямая и достаточно тесная связь.

2. Вычислим параметры уравнений регрессии по МНК, т.е. используя систему нормальных уравнений: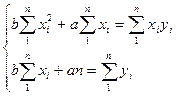

1) Параметры линейной регрессии находим из системы нормальных уравнений:

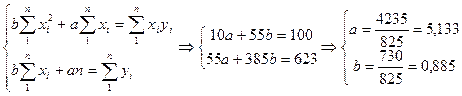
	Фактические данные
№	X	Y	x^2	xy
Суммы

Уравнение линейной регрессии имеет вид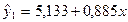

2) Найдем параметры уравнения регрессии 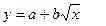, нелинейного относительно объясняющей переменной. Используем метод замены переменной: пусть .

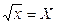Получаем линейное уравнение регрессии 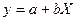, параметры которого определяем из уже известной нам системы нормальных уравнений:

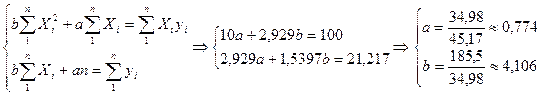
	Фактические данные	X1
№	X	Y	x^0,5	X^2	Xy
			1,41	2,00	9,90
			1,73	3,00	15,59
			2,00	4,00	24,00
			2,24	5,00	22,36
			2,45	6,00	29,39
			2,65	7,00	29,11
			2,83	8,00	33,94
			3,00	9,00	39,00
			3,16	10,00	37,94
Суммы			22,47	54,99	243,22

Уравнение с корнем квадратным имеет вид: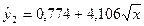

3) Параметры уравнения регрессии 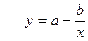также нелинейные относительно объясняющей переменной. Используем метод замены переменной: пусть .

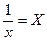Получаем линейное уравнение регрессии 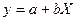, параметры которого определяем из уже известной нам системы нормальных уравнений:

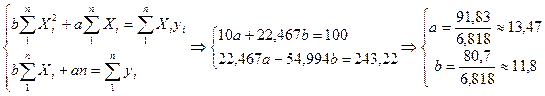
Таблица вычислений сумм для третьей модели

	Фактические данные	X2
№	X	Y	1/x	X^2	Xy
			0,50	0,25	3,50
			0,33	0,11	3,00
			0,25	0,06	3,00
			0,20	0,04	2,00
			0,17	0,03	2,00
			0,14	0,02	1,57
			0,13	0,02	1,50
			0,11	0,01	1,44
			0,10	0,01	1,20
Суммы			2,93	1,54	21,22

Уравнение 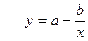равносторонней гиперболы имеет вид: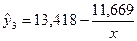

Получены следующие уравнения регрессии:

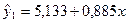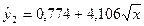1) 2) 3)

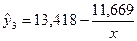
3) Для оценки качества уравнений вычислим для каждого случая индекс детерминации

.

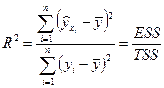Вычисления сумм выполним в таблице:

Факт. данные	Предсказанные значения Y по построенным моделям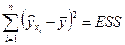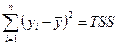
x	y	y1	y2	y3	ESS1	ESS2	ESS3	TSS
		6,018	4,88	1,751	15,86	26,21	68,05
		6,903	6,581	7,586	9,591	11,69	5,83
		7,788	7,886	9,53	4,893	4,47	0,221
		8,673	8,986	10,5	1,761	1,028	0,253
		9,558	9,955	11,09	0,195	0,002	1,18
		10,44	10,83	11,48	0,196	0,692	2,176
		11,33	11,64	11,75	1,764	2,681	3,073
		12,21	12,39	11,96	4,897	5,7	3,847
		13,1	13,09	12,12	9,598	9,56	4,509
		13,98	13,76	12,25	15,86	14,12	5,076
Yср=					64,62	76,16	94,21
				R^2	0,646	0,762	0,942

Таким образом,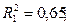

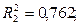
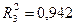
Вывод: третья модель является лучшей из построенных, так как имеет наибольшую прогностическую силу.

Величина коэффициента детерминации третьей модели говорит о том, что изменение ежегодного потребления бананов (Y) на 94,2% объясняется годовым доходом американской семьи (X).