Построение двойственной задачи

Составим двойственную к задаче использования сырья (1.4).

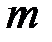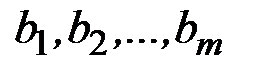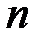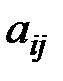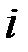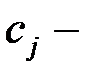Имеется видов сырья в количестве , которые используются для изготовления видов продукции. Известно: – расход -го вида сырья на единицу -й продукции; прибыль от реализации единицы -го вида продукции. Составить план выпуска продукции, обеспечивающий максимальную прибыль. Математическая модель данной задачи имеет вид (в матричной форме):

;

;

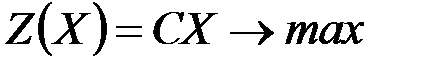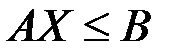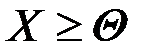. (2.1)

Здесь 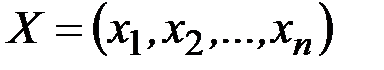, 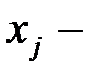объём производства -го вида продукции.

Предположим, что второй потребитель хочет перекупить сырьё. Составим двойственную задачу, решение которой позволит определить условия продажи сырья. Введём вектор оценок (цен) видов сырья 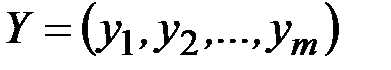. Тогда затраты на приобретение сырья в количестве 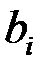равны 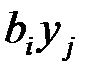. Второму производителю выгодно минимизировать суммарные затраты на приобретение всех видов сырья, поэтому целевая функция имеет вид

.

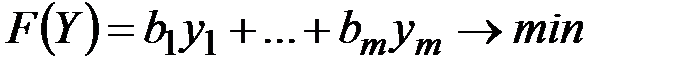Первому производителю невыгодно продавать сырьё, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие -й продукции меньше прибыли 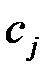, получаемой при реализации этого изделия, т.е.

, .

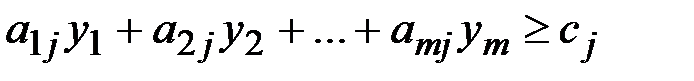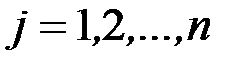В матричной форме задача имеет следующий вид:

;

;

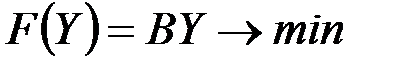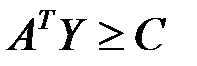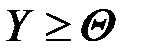. (2.2)

Таким образом, связь между исходной и двойственной задачами состоит в том, что коэффициенты 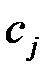целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены 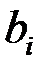системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи.

В теории двойственности используются 4 пары двойственных задач:

Исходная задача	Двойственная задача
Симметричные пары
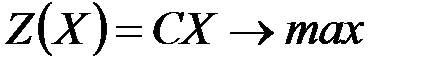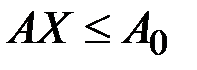1.	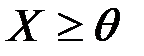1.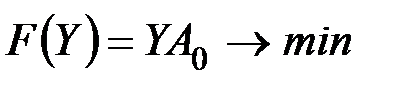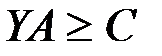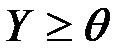
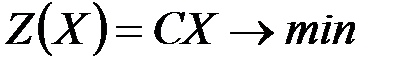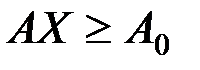2.	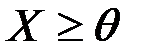2.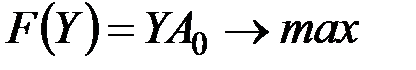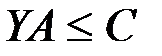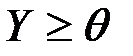
Несимметричные пары
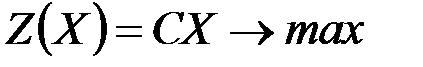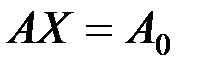3.	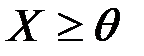3.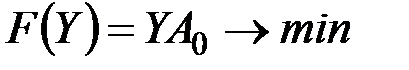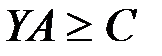
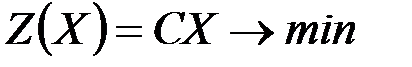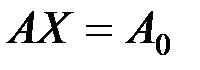4.	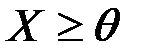4. ,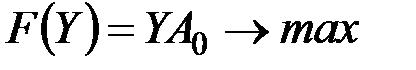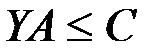

где

С = (c₁, c₂, …, c_n); Y = (y₁, y₂, …, y_m);

; ; .

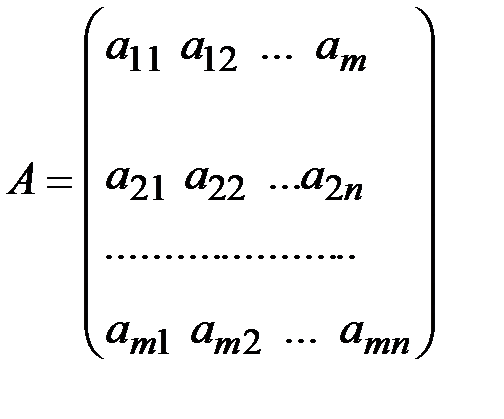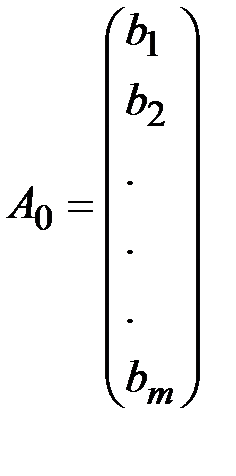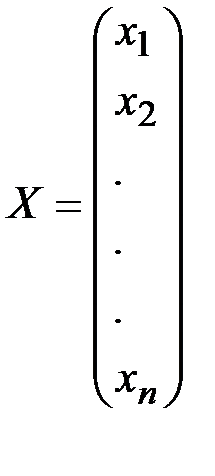Общие правила составления двойственных задач:

Правило 1. Во всех ограничениях исходной задачи свободные члены должны находиться в правой части, а члены с неизвестными – в левой.

Правило 2. Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.

Правило 3. Если знаки неравенств в ограничениях исходной задачи « 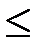», то целевая функция 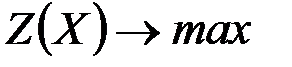, а если « 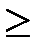», то .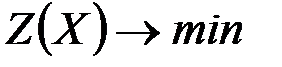

Правило 4. Каждому ограничению исходной задачи соответствует неизвестное в двойственной задаче, при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-равенству, может быть любого знака.

Правило 5. Целевая функция двойственной задачи имеет вид

,

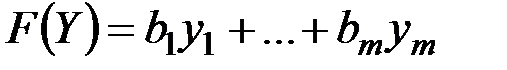где 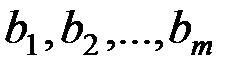– свободные члены в ограничениях исходной задачи.

Правило 6. Целевая функция 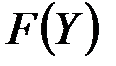должна оптимизироваться противоположным по сравнению с 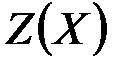образом.

Правило 7. Каждому неизвестному х_j , j = 1, 2, …, n исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих n ограничений (вместе с условиями неотрицательности неизвестных y_i , соответствующих ограничениям-неравенствам исходной задачи) образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными y₁, y₂, …, 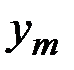– в левых.

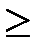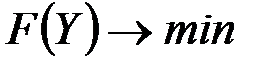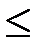Все знаки неравенств имеют вид « », если , и « », то 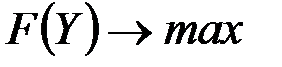.