Отчет по лабораторной работе № 5
Настройка зубострогального станка модели 526 на нарезание прямозубых конических колес
Исходные данные: m = мм; Z = ; Zс = ; δ = град.; δе = град.;
δf = град.; Rе = мм; dе = мм; nм = мм; b = мм; h = мм; h// = мм.
Обрабатываемый материал:__________
Таблица 5.6
| Содержание работы | Выполнение | ||
| кинематические уравнения | сменные колеса | ||
| Подбор сменных колес гитары двойных ходов ползунов | |||
| Подбор сменных колес гитары деления | |||
| Подбор сменных колес гитары обката | |||
| Подбор сменных колес угла обката | |||
| Подбор сменных колес гитары подач | |||
| Толщина зуба На переднем торце | по расчету | по результатам измерения | |
| На заднем торце | |||
Дата ________ Подпись студента:_____________
Подпись преподавателя:_____________
Вопросы для самопроверки и задания
1. Какой принцип работы зубострогального станка 526 используется при черновом и чистовом нарезании зубчатых колес?
2. Какие основные узлы станка 526, дать их назначение.
3. Показать все кинематические цепи зубострогального станка, их взаимосвязь.
4. В чем заключается условие расчета цепи движения резания?
5. Как осуществляется расчет цепи деления?
6. Написать условие расчета цепи обката.
7. Каков принцип работы дифференциала имеющегося на станке?
8. Из каких механизмов состоит кинематическая цепь подач, показать
порядок ее настройки?
Варианты заданий для нарезания конического зубчатого колеса
Таблица 5.7
Варианты заданий на настройку станка модели 526
| № п/п | m | Zр | Zc | δ | δe | δi | Re | de | Lм |
| 2,5 | 26°34׀ | 28°29׀ | 24°39' | 83,89 | 79,46 | 75,78 | |||
| 2,5 | 53°48' | 56°03׀ | 51°06' | 63,50 | 105,45 | 61,70 | |||
| 2,5 | 36°26' | 38°38׀ | 33°18' | 65,25 | 81,52 | 77,00 | |||
| 2,5 | 53°34' | 55°46׀ | 50°56׀ | 65,25 | 107,98 | 62,72 | |||
| 2,5 | 36°39' | 38°47' | 34°05' | 67,00 | 84,00 | 78,28 | |||
| 2,5 | 53°21' | 55°29׀ | 30°47' | 67,00 | 110,48 | 64,00 | |||
| 2,5 | 37°16׀ | 39°15' | 34°53' | 72,25 | 91,48 | 81,98 | |||
| 2,5 | 52°44' | 54°43' | 50°21' | 72,25 | 118,02 | 67,75 | |||
| 2,5 | 39°41' | 41°34' | 37°26' | 76,32 | 101,35 | 83,15 | |||
| 2,5 | 50°19' | 52°12' | 48°04' | 76,32 | 120,70 | 72,82 | |||
| 2,5 | 37°09' | 39°55' | 33°50' | 62,10 | 79,77 | 73,67 | |||
| 52°51' | 55°37' | 49°32' | 62,10 | 102,63 | 61,10 | ||||
| 37°04' | 39°0б' | 34°38' | 84,60 | 106,80 | 91,70 | ||||
| 52°56' | 54°58- | 50°30' | 84,60 | 138,63 | 74,60 | ||||
| 37°14' | 39°03' | 35°06' | 94,20 | 118,77 | 99,20 | ||||
| 52°46' | 54°35' | 50°35' | 94,20 | 153,63 | 80,63 | ||||
| 34°05' | 36°52' | 30°44' | 71,86 | 86,31 | 83,54 | ||||
| 3,5 | 55°55' | 58°42' | 52°34' | 71,86 | 122,92 | 63,38 | |||
| 3,5 | 34°26' | 37°08' | 31°12' | 74,21 | 89,78 | 85,29 | |||
| 3,5 | 55°34' | 58°16' | 52°20' | 74,22 | 126,46 | 65,10 | |||
| 3,5 | 37°07' | 39°35' | 34°09' | 74,22 | 103,66 | 88,62 | |||
| 3,5 | 52°53' | 55°21' | 49°55' | 81,20 | 133,74 | 72,20 | |||
| 3,5 | 36°52' | 39°25' | 33°49' | 78,75 | 100,10 | 86,90 | |||
| 3,5 | 53°08' | 55°41' | 50°05' | 78,75 | 130,20 | 70,45 | |||
| Продолжение таблицы 5.7 | |||||||||
| 3,5 | 36°07' | 33°37' | 33°07' | 91,60 | 114,48 | 97,64 | |||
| 53°53' | 36°23' | 50°53' | 91,60 | 152,72 | 76,76 | ||||
| 36°38' | 38°69' | 33°48' | 97,20 | 122,40 | 101,64 | ||||
| 53°22' | 55°43' | 50°32' | 97,20 | 160,76 | 80,80 | ||||
| 56°33' | 39°10' | 34°08' | 99,96 | 126,40 | 103,60 | ||||
| 53°07' | 55°24' | 50°22׀ | 99,96 | 164,80 | 82,84 |
Вариант: 1…3 длина зуба b=25 мм; 4…7 - b=40 мм; 8…10 - b=35 мм; 11…14 b=55 мм; 15…18 b=20 мм; 19…22 - b=60 мм; 23…25 b=45 мм; 26…30 - b=70 мм;
Вариант: 1…5 материал – сталь 20; 6…10 – сталь 40Х; 11…15 – сталь 45; 16…20 – СТАЛЬ 20Х; 21…25 – сталь 50; 26…30 - чугун.
Приложение
Методы подбора числа зубьев сменных зубчатых колес
Существует несколько методов подбора числа зубьев сменных зубчатых колес: непрерывных дробей; подбора зубьев колес на логарифмической линейке; разложения на множители.
Метод непрерывных дробей
Если нет под рукой справочников с таблицами перевода десятичных
дробей в обыкновенные дроби с числителями и знаменателями, удобными для подбора чисел зубьев сменных колес, можно воспользоваться методом непрерывных дробей.
Пример. Пусть мы получим передаточное отношение, равное 1,097074. Требуется подобрать колеса с числами зубьев из имеющихся в комплекте. Преобразуем число 1,097074 в непрерывную дробь, выразив вначале в виде обыкновенной дроби:
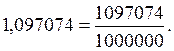
Чтобы превратить обыкновенную дробь в непрерывную, необходимо числитель дроби разделить на знаменатель. Получим первое частное и остаток от деления.
1,097074: 1000000 = 1 (первое частное) и 97074 (первый остаток). После этого делим знаменатель дроби на первый остаток, получим второе частное и второй остаток.
97074: 29260 = 3 (третье частное) и 9294 (третий остаток). Продолжаем делить каждый предыдущий остаток на вновь получаемый.
29260: 9294 = 3 (четвертое частное) и 1378 (четвертый остаток).
9294: 1378 = 6 (пятое частное) и 1026 (пятый остаток).
1378: 1026 = 1 (шестое частное) и 352 (шестой остаток).
Обычно для таких дробей точность будет достаточной уже на шестом, седьмом действиях деления. За знаменатели каждого числа непрерывной дроби примем полученные частные:
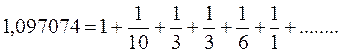 .
.
Для получения приближенного значения дроби непрерывную дробь прерывают на каком-либо члене, отбрасывая остальные.
В нашем примере, отбросив члены дроби со второго, получим первое приближение:
1. 1.
Прервав непрерывную дробь на втором члене, получим второе приближение:
2. 1 +1/10 и т.д.
3. 1 + 1/10 + 1/3. 4. 1+ 1/10 + 1/3 + 1/3.
5. 1 + 1/10 + 1/3 + 1/3 +1/6.
6. 1+ 1/10 + 1/3 + 1/3 + 1/6 +1/1.
Теперь превратим каждую прерванную дробь в обыкновенную:
2. (1+1) 10, 11/10.
Для того чтобы найти третью и каждую следующую за ней обыкновенную дробь, необходимо числитель и знаменатель полученной дроби умножить на знаменатель следующего члена непрерывной дроби и прибавить к числителю произведения числитель, а к знаменателю произведения – знаменатель предыдущей дроби:
3. 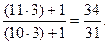 5.
5. 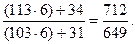
4. 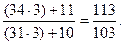 6.
6. 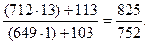
Все найденные дроби нечетного порядка меньше, а четного порядка – больше непрерывной дроби. Действительная величина непрерывной дроби будет находиться между двумя последовательными приближенными значениями. При этом новое приближенное значение будет меньше отличаться от непрерывной дроби, чем предшествующее.
Останавливаясь на отдельных приближенных значениях, необходимо производить их разложение на простейшие множители, а затем подбирать соответствующие сменные колеса из имеющегося комплекта.
Полученные дроби в десятичном выражении имеют следующие значения:
1. 1 = 1,0. 4 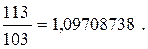
2. 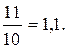 5.
5. 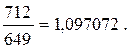
3. 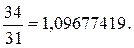 6.
6. 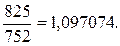
Высокую точность дает дробь: 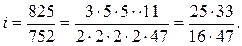
Умножив числитель и знаменатель на 3, получим: 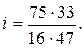
(такие колеса в комплекте имеются).
