Перечень программных вопросов по пройденному курсу и соответствующих итоговым тестам
1. Случайные события. Классификация событий.
2. Классическое определение вероятности.
3. Статистическое определение вероятности.
4. Геометрическое определение вероятности.
5. Элементы комбинаторики. Правило суммы. Правило произведения.
6. Виды комбинаций: размещения из n элементов по m, сочетания из n элементов
по m, перестановки из n элементов.
7. Формула для вычисления числа размещений из n элементов по m.
8. Формула для вычисления числа сочетаний n элементов по m.
9. Формула для вычисления числа перестановок из n элементов.
10. Непосредственное вычисление вероятностей.
11. Действия над событиями. Сумма, произведение и разность событий.
12. Теорема сложения вероятностей.
13. Условная вероятность события.
14. Теорема умножения вероятностей.
15. Независимые события. Теорема умножения вероятностей независимых событий.
16. Вероятность появления хотя бы одного события.
17. Вероятность суммы двух совместных событий.
18. Формула полной вероятности.
19. Формула Байеса.
20. Формула Бернулли.
21. Наивероятнейшее число появления события.
22. Локальная теорема Муавра-Лапласа.
23. Интегральная теорема Муавра-Лапласа.
24. Формула Пуассона.
25. Вероятность отклонения относительной частоты от постоянной вероятности в
независимых испытаниях.
26. Понятие случайной величины.
27. Закон распределения дискретной случайной величины.
28. Математические операции над случайными величинами.
29. Математическое ожидание дискретной случайной величины.
30. Свойства математического ожидания.
31. Дисперсия дискретной случайной величины.
32. Свойства дисперсии.
33. Формула для вычисления дисперсии.
34. Среднее квадратическое отклонение.
- Функция распределения случайной величины.
- Свойства функции распределения.
- Непрерывные случайные величины.
- Плотность вероятности.
- Мода случайной величины.
- Свойства плотности вероятности.
- Числовые характеристикинепрерывных случайных величин.
- Формула для математического ожидания непрерывной случайный величины.
- Формула для дисперсии непрерывной случайный величины.
- Медиана случайной величины.
- Начальные и центральные моментыслучайных величин.
- Коэффициент асимметрии случайной величины.
- Эксцесс случайной величины.
48. Биноминальныйзакон распределения.
- Математическое ожидание и дисперсия случайной величины, распределенной по
биноминальномузакону.
- Закон распределения Пуассона.
- Математическое ожидание и дисперсия случайной величины, распределенной по
закону Пуассона.
- Геометрическое распределение.
- Математическое ожидание и дисперсия случайной величины, имеющей
геометрическое распределение.
- Равномерный закон распределения.
- Функция распределения случайной величины, распределенной по
равномерному закону.
- Математическое ожидание и дисперсия случайной величины, распределенной по
равномерному закону.
- Показательный закон распределения.
- Функция распределения случайной величины, распределенной по показательному
закону.
- Математическое ожидание и дисперсия случайной величины, распределенной по
показательному закону.
- Нормальный закон распределения.
- Нормальная кривая.
- Свойства случайной величины, распределенной по нормальному закону.
- Коэффициент асимметрии и эксцесс случайной величины, распределенной по
нормальному закону.
64. Неравенство Чебышева.
65. Теорема Чебышева.
66. Теорема Бернулли.
67. Графическое изображение вариационного ряда: полигон, гистограмма, кумулята.
- Эмпирическая функция распределения.
- Свойства эмпирической функции распределения.
- Средние величины. Средняя арифметическая вариационного ряда и ее свойства.
- Мода и медиана вариационного ряда.
- Показатели вариации. Среднее линейное отклонение вариационного ряда.
- Дисперсия вариационного ряда.
- Основные свойства дисперсии.
- Формула для вычисления дисперсии.
- Среднее квадратическое отклонение.
- Условные варианты. Упрощенный способ расчета средней арифметической и
дисперсии.
- Начальные моменты вариационного ряда.
- Центральные моменты вариационного ряда.
- Коэффициент асимметрии вариационного ряда.
- Эксцесс вариационного ряда.
82. Генеральная и выборочная совокупности.
83. Несмещенная оценка.
84. Эффективная оценка.
85. Состоятельная оценка.
86. Метод моментов для нахождения оценки неизвестного параметра.
87. Метод максимального правдоподобия для нахождения оценки неизвестного
параметра.
88. Оценка метода моментов для параметра 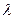 закона Пуассона.
закона Пуассона.
89. Оценка метода максимального правдоподобия для вероятности р события А.
90. Оценки метода максимального правдоподобия для параметров а и 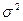 нормального закона распределения по данным выборки.
нормального закона распределения по данным выборки.
91. Оценка генеральной средней по выборочной средней.
92. Оценка генеральной дисперсии по исправленной выборочной дисперсии.
93. Понятие интервального оценивания.
94. Доверительная вероятность (надежность). Доверительный интервал.
95. Доверительные интервалы для оценки математического ожидания нормально
распределенной случайной величин при известном 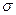 для заданной
для заданной
надежности 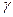 .
.
96. Объем выборки.
97. Доверительные интервалы для оценки математического ожидания нормальной
случайной величины по её выборке объёма nпри неизвестном 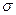 для заданной
для заданной
надежности 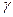
98. Доверительные интервалы для оценки среднего квадратичного отклонения
нормально распределенной случайной величины для заданной надежности 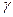 .
.
99.Функциональная, статистическая и корреляционная зависимости.
100.Условные средние.
101. Корреляционная зависимость.
102. Две основные задачи теории корреляции.
103. Отыскание параметров выборочного уравнения прямой линии регрессии по
несгруппированным данным.
104. Уравнение регрессии.
105. Линия регрессии.
Глоссарий
| № | Новые понятия | Содержания |
| Формула классической вероятности | 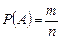 , где , где 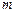 - число элементарных событий, благоприятствующих событию А, - число элементарных событий, благоприятствующих событию А, 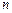 -общее число элементарных событий. -общее число элементарных событий. | |
| Аксиомы вероятности | 1) 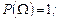 2 2 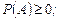 3) 3) 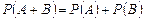 , если А и В несовместные события. , если А и В несовместные события. | |
| Условная вероятность события А при условии, что событие В произошло | число равное 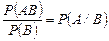 . . | |
| Независимые события А и В | 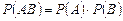 . . | |
| Формула полной вероятности | 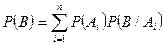 . . | |
| Формула Байеса | 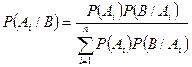 | |
| Схема Бернулли | 1) 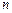 независимых испытаний; 2) каждое испытание имеет два исхода: удача и неудача; 3) вероятность наступления удачи в отдельном испытании постоянна и равна независимых испытаний; 2) каждое испытание имеет два исхода: удача и неудача; 3) вероятность наступления удачи в отдельном испытании постоянна и равна 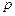 . . | |
Вероятность наступления k раз рассматриваемого события в 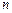 испытаниях испытаниях |  ; ; 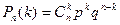 - формула Бернулли; - формула Бернулли; 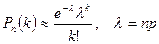 – формула Пуассона; – формула Пуассона; 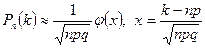 – локальная формула Лапласа; – локальная формула Лапласа; 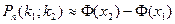 , , 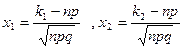 – интегральная формула Лапласа. – интегральная формула Лапласа. | |
| Случайная величина | числовая функция, определенная на пространстве элементарных событий. | |
| Дискретная случайная величина | случайная величина, имеющая счетное множество значений. | |
| Математическое ожидание дискретной величины | 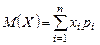 . . | |
| Дисперсия дискретной случайной величины | 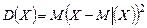 или или 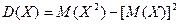 . . | |
| Среднее квадратичное отклонение случайной величины | 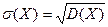 . . | |
| Функция распределения вероятностей случайной величины Х | функция 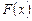 , определенная равенством , определенная равенством 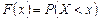 , т.е. вероятность того, что случайная величина Х принимает значения меньше чем х. , т.е. вероятность того, что случайная величина Х принимает значения меньше чем х. | |
| Непрерывная случайная величина | случайная величина Х, для которой функция распределения вероятностей 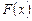 непрерывна. непрерывна. | |
| Плотность распределения вероятностей | функция 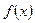 , удовлетворяющая равенству , удовлетворяющая равенству 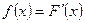 , где , где 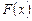 – функция распределения вероятностей. – функция распределения вероятностей. | |
| Математическое ожидание непрерывной случайной величины | 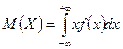 ; ; | |
| Дисперсия непрерывной случайной величины | 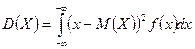 или или 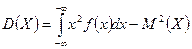 . . | |
| Равномерное распределение вероятностей в отрезке [а, b] | плотность вероятности постоянна в этом отрезке и равна нулю вне него: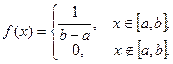 | |
| Нормальное распределение вероятностей случайной величины Х | закон нормального распределения вероятностей определяется плотностью вероятности 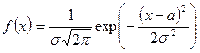 , где , где 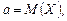 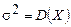 . . | |
| Неравенство Чебышева | пусть Х – случайная величина, М(Х) – ее математическое ожидание, D(Х) – дисперсия, 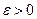 –число. Тогда –число. Тогда 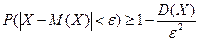 или или 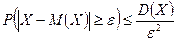 . . | |
| Закон больших чисел. Теорема Чебышева | пусть 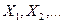 – последовательность независимых случайных величин, дисперсии которых ограничены некоторым числом – последовательность независимых случайных величин, дисперсии которых ограничены некоторым числом 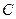 , т.е. , т.е. 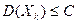 для всех для всех 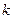 . Тогда для любого . Тогда для любого 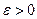 верны соотношения верны соотношения 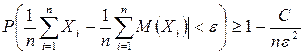 ; ; 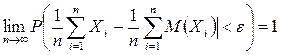 . . | |
| Генеральная совокупность | совокупность всех однородных объектов, подлежащих изучению. | |
| Выборочная совокупность (выборка) | совокупности объектов, случайно отобранных из генеральной совокупности. | |
| Объем совокупности | число ее объектов. | |
| Вариационный ряд, варианты | последовательность наблюдаемых значений 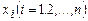 , записанных в возрастающем порядке. Значение , записанных в возрастающем порядке. Значение 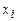 называется вариантой. называется вариантой. | |
| Относительная частота | 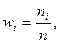 где где 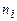 - частота появления значений - частота появления значений 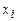 , , 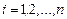 . . | |
| Статистические распределение выборки | соответствие между вариантами и их частотами (или относительными частотами). | |
| Генеральная средняя (выборочная средняя) | среднее арифметическое значений генеральной совокупности (выборочной совокупности) признака Х. | |
Выборочная дисперсия 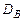 . . | 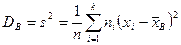 , где , где 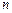 – объем выборки, – объем выборки, 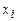 – варианты, – варианты, 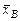 -–средняя выборочная, -–средняя выборочная, 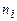 – частота варианты – частота варианты 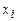 . . | |
Исправленная выборочная дисперсия 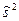 . . | 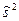 = = 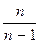 s2 . s2 . | |
Доверительная вероятность, илинадежность 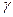 , оценки , оценки 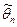 неизвестного параметра неизвестного параметра 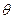 | вероятность 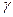 , с которой осуществляется неравенство , с которой осуществляется неравенство 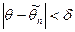 , т.е. , т.е. 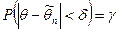 . . | |
| Доверительный интервал | интервал 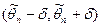 , который покрывает неизвестный параметр , который покрывает неизвестный параметр 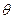 с заданной надежностью с заданной надежностью 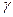 . . |
Общая шкала оценки знаний
| Буквенная оценка | Цифровой эквивалент баллов | %-е содержание усвоения учебной дисциплины | Оценка по традиционной системе |
| A | 4,0 | 95-100 | отлично |
| A- | 3,67 | 90-94 | |
| B+ | 3,33 | 85-89 | хорошо |
| B | 3,0 | 80-84 | |
| B- | 2,67 | 75-79 | |
| C+ | 2,33 | 70-74 | удовлетворительно |
| C | 2,0 | 65-69 | |
| C- | 1,67 | 60-64 | |
| D+ | 1,33 | 55-59 | |
| D | 1,0 | 50-54 | |
| F | 0-49 | неудовлетворительно |
