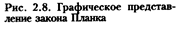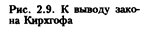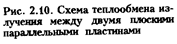Основные законы теплового излучения

Законы теплового излучения получены применительно к идеальному абсолютно черному телу и условиям термического равновесия.

Закон Планка. Разрабатывая квантовую теорию излучения, М. Планк (1900 г.) теоретически установил зависимость спектральной плотности потока излучения абсолютно черного тела от абсолютной температуры и длины волны:

где λ. - длина волны, м; 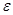- основание натурального логарифма; 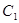= 3,74 • 10'¹⁶, Вт/м² — первая постоянная Планка; 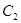= 1,44 • 10², м • К - вторая постоянная Планка.

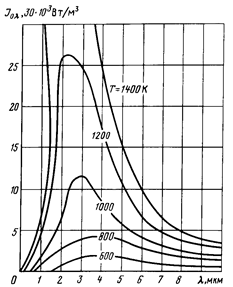
На рис. 2.8 дано графическое представление закона Планка. Из приведенных на графике изотерм видно, что интенсивность излучения вначале, на участке у коротких волн, быстро возрастает до максимума, а затем медленно убывает. При одной и той же длине волны интенсивность излучения тем больше, чем выше температура тела.

Закон смещения (Вина). На основании термодинамического исследования черного равновесного излучения В. Вин в 1893 г. установил следующую связь между абсолютной температурой T и длиной волны 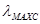, которой соответствует максимальная интенсивность излучения:

Уравнение является математической формулировкой закона смещения (Вина), из которого следует, что при увеличении температуры равновесной системы максимум спектральной объемной плотности энергии равновесного излучения (интен­сивности излучения) 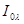смещается в сторону более коротких длин волн. Например, для солнечного излучения (T≈6000 К) максимум интенсивности падает на видимый участок спектра ( 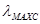⁼ 0.5 мкм). Для температур, встречающихся в техни­ческих устройствах (ниже 2000 К), максимум интенсивности приходится на тепловые (инфракрасные) лучи.

Для того, чтобы определить конкретные значения 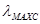при задании различных температур Т, необходимо знать величину b, называемую постоянной Вина. Теоретические исследования Планка позволили провести независимое определение b, и в соответствии с современными данными ее значение равно: b = 2,8978 • 10³ м • К.

Подставив значение произведения 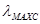• Т из уравнения (2.94) в формулу Планка, получим для максимума интенсив­ности ( 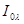) , следующее уравнение:

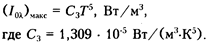
Таким образом, максимальная интенсивность излучения пропорциональна пятой степени температуры абсолютно черного тела.

Закон Стефана — Больцмана. Закон Стефана - Больцмана устанавливает зависимость плотности потока интегрального полусферического излучения от температуры. Эта зависимость задолго до появления квантовой теории Планка впервые экспериментально (путем изменений собственного излучениямодели черного тела) была установлена И. Стефаном (1879 г.). Позднее (в 1884 г.) она теоретически (исходя из законов термодинамики) была получена Л. Больцманом. Поэтому закон получил объединенное название закона Стефана - Больцмана, который может быть получен и при использовании закона Планка. Закон Стефана - Больцмана для поверхностной плотности потока интегрального излучения Е (Вт/м²) можно выразить следующим образом:

В результате интегрирования получаем

где о = 5,67 • 10 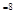, Вт/( м 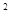К)- константа излучения абсолютно черного тела.

В технических расчетах для удобства использования константу увеличивают в 10⁸ раз, а для компенсации в фор­муле температуру делят на 100. Тогда закон Стефана - Больц­мана приобретает вид

где Со = 5,67 Вт/( м 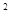• К 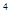) - коэффициент излучения абсолютно черного тела.

Закон Стефана - Больцмана может быть применен и к се­рым телам. В этом случае используется положение о том, что у серых тел, так же как и у черных, собственное излучение пропорционально абсолютной температуре в четвертой степе­ни, но энергия излучения меньше, чем энергия излучения черного тела при той же температуре.

Для серых тел этот закон имеет вид

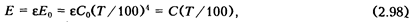
гд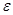е = Е/Е 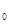= С/Со < 1 - интегральная степень черноты серого тела, представляющая собой относительную излучательную способность серого тела.

Таким образом, степень черноты представляет собой отношение излучательной способности реального серого тела к излучательной способности абсолютно черного тела при той же температуре. Степень черноты (относительный коэффи­циент излучения) серого тела зависит от природы тела, температуры, состояния поверхности и в большинстве случаев определяется экспериментальным путем.

Закон Кирхгофа. Закон Кирхгофа устанавливает связь между излучательной и поглощательной способностями тела. В 1860 г. немецким физиком Г. Кирхгофом исходя из второго начала термодинамики теоретически было установлено, что отношение излучательной способности абсолютно черного тела к его поглощательной способности является функцией только длины волны и абсолютной температуры. Эта функция уни­версальна для всех тел, находящихся при одинаковой темпе­ратуре. Исследованиями Кирхгофа было положено начало количественной теории теплового излучения.

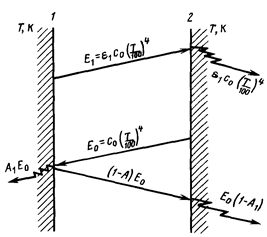
Эту связь можно получить, рассматривая лучистый обмен между двумя поверхностями

(рис. 2.9). Пусть на рис. 2.9 поверхность тела / будет серой и темпе­ратура ее равна T; поверхность тела 2 - абсолютно черная с одинаковой температурой во всех точках. Поверхность тела 2 излучает на тело 1 энергию Е 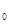= Со (Г/100)⁴. Часть ее 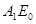поглощается телом 1, которое, в свою очередь, излучает энергию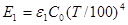

При равенстве температур обеих поверхностей тепловой поток, излучаемый серой поверхностью, должен быть равен тепловому потоку, который она поглощает.

Следовательно,

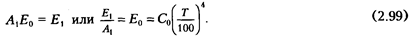
Полученная закономерность справедлива для любых других серых тел, поглощательные способности которых соответст­венно равны 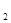A ,A 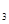и т.д.

Поэтому уравнение, выражающее закон Кирхгофа, можно записать в общем виде:

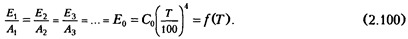
На основании этого уравнения можно сделать вывод, что для любого тела отношение его излучательной способности к поглощательной равно излучательной способности абсолютно черного тела при той же температуре и зависит только от температуры.

Подставив в уравнении вместо значений

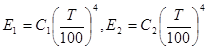И Т.Д.

и сократив обе части равенства на (T/100)⁴, получим

Если сравнить уравнения (2.99), (2.100) и 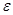= Е/Е 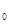= С/Со, то окажется, что А = 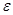, т.е. поглощательная способность тела и степень черноты численно равны друг другу.

Из уравнения (2.101) вытекает, что излучательная способ­ность всех тел меньше излучательной способности абсолютно черного тела при той же температуре.

Частные случаи теплообмена излучением. На основании законов лучистого теплообмена можно вывести расчетные уравнения для лучистого теплообмена между телами.

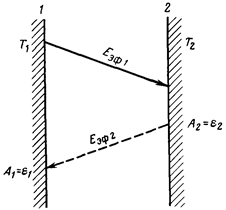
Рассмотрим теплообмен излучением между двумя парал­лельными пластинами (серыми телами) неограниченных размеров, разделенными прозрачной средой (рис. 2.10).

Для каждой поверхности заданы постоянные во времени температуры 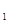Т и Т 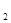, поглощательные способности тел 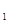A , и A 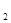. Выведем формулу для определения количества теплоты 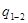, передаваемой от первой пластины ко второй.

Лучистый теплообмен между телами количественно характе­ризуется потоком результирующего излучения. Для абсолютно черного тела на основании (2.98) получаем

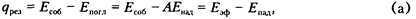
откуда

Исключив из (б) E . запишем

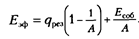
Для системы плоскопараллельных поверхностей эффектив­ное излучение каждого из рассматриваемых тел в соответст­вии с уравнением (2.98) можно представить соотношениями

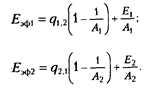
Выражение для результирующего потока с учетом того, что при стационарном тепловом режиме 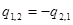, запишется так:

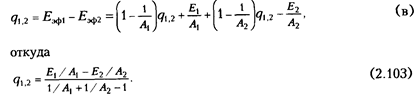
Теперь найдем ончательное расчетное выражение для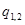

Для этого подставим в уравнение (а) вместо плотностей потоков собственного излучения их выражения по закону Стефана - Больцмана через заданные температуры:

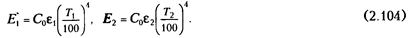
Тогда получим

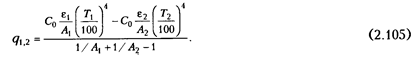
Если положить 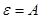, то формула упрощается:

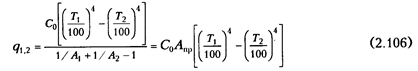
или

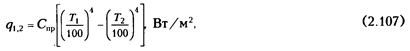
где A 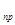— приведенная поглощательная способность; для рассматриваемой геометрической системы тел она выражается зависимостью

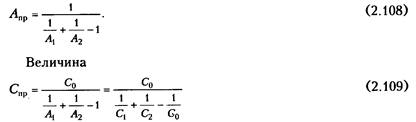
носит название приведенного коэффициента излучения и измеряется в Вт/(м 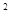К⁴). Приведенный коэффициент излучения характеризует интенсивность результирующего излучения для рассматриваемой системы двух или произ­вольного числа тел. Количественно он равен потоку резуль­тирующего излучения, отнесенному к единице поверхности рассматриваемого тела, единице времени и единице перепада температур между этим телом и окружающими его телами вчетвертой степени. Значение полученного коэффициента излу­чения зависит от оптико-геометрических свойств данной излу­чающей системы тел. Полный результирующий поток выра­зится зависимостью

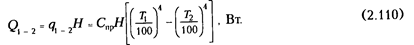
Зависимость показывает, что результирующий поток прямо пропорционален приведенному коэффициенту излучения, площади поверхности тела и разности температур в четвер­той степени. В процессах же теплопроводности и конвекции тепловой поток пропорционален разности температур в пер­вой степени. Этим обстоятельством объясняется более зна­чительное влияние лучистого теплообмена по сравнению с указанными процессами при высоких температурах.

Для серых тел равенство поглощательной способности и степени черноты 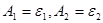имеет место не только при температурном равновесии (закон Кирхгофа), но и в условиях лучистого теплообмена, когда 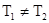. Поэтому, если подставить в уравнение выражения 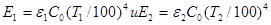и учесть, что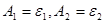

то можно получить после преобразования соотношение

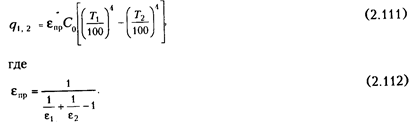
Уравнение есть расчетная формула для лучистого теплообмена между параллельными серыми плоскостями. Коэффициент 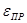называется приведенной степенью черноты системы тел, между которыми происходит процесс лучистого теплообмена; значение его может изменяться от 0 до 1.