Значимость коэффициента корреляции
Для проведения полноценного статистического анализа свойств генеральной совокупности, основанных на коэффициенте корреляции, необходимо знать ее статистические свойства. Это позволит судить о точности приближения (4.24) к неизвестному истинному значению коэффициента корреляции r, строить статистические критерии для проверки различных гипотез о численных значениях анализируемого коэффициента корреляции.
В частности, какую величину выборочного коэффициента корреляции следует считать достаточной для статистически обоснованного вывода о наличии корреляционной связи между исследуемыми переменными? Ведь надежность статистических характеристик, в том числе и r, ослабевает с уменьшением объема соответствующей выборки, а потому принципиально возможны случаи, когда отклонения от нуля полученной величины выборочного коэффициента корреляции r оказывается статистически незначимым, т.е. целиком обусловленным случайными колебаниями выборки, на основании которой он вычислен. Ответить на этот вопрос позволяет знание закона распределения вероятностей r.
В случае совместной нормальной распределенности исследуемых переменных и при достаточно большом объеме выборки n (а именно при n>200) распределение r можно считать приближенно нормальным со средним, равным своему теоретическому значению r, и дисперсией
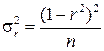 . (4.26)
. (4.26)
Однако следует учитывать, что при малых значениях n и r, близких к ±1, это приближение оказывается очень грубым. Кроме того, при малых n следует принимать во внимание, что величина r является смещенной оценкой своего теоретического значения r, в частности
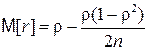 . (4.27)
. (4.27)
В качестве критерия проверки нулевой гипотезы 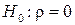 против альтернативной
против альтернативной 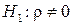 используется величина
используется величина
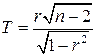 . (4.28)
. (4.28)
Эта величина при относительно хорошей степени приближения к нормальному распределению и при малых значениях |r| приблизительно распределена по закону распределения Стьюдента с n=n–2 степенями свободы. Поэтому, если окажется, что 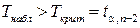 , то нулевая гипотеза об отсутствии корреляционной связи между X и Y отвергается с вероятностью ошибиться, равной a.
, то нулевая гипотеза об отсутствии корреляционной связи между X и Y отвергается с вероятностью ошибиться, равной a.
Пример 4.2. Проверить значимость коэффициентов корреляции в примере 4.1 на уровне значимости a=0,05.
Решение. Для примера 4.1 n=7 и r=0,9389. Вычислим наблюдаемое и критическое значения критерия Стьюдента
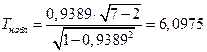 и
и 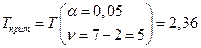 .
.
Поскольку 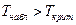 , то коэффициент корреляции существенно отличается от нуля. â
, то коэффициент корреляции существенно отличается от нуля. â
Пример 4.3. Взяты 10 наблюдений показателей инфляции и безработицы в США за 1931-1940 годы, для них рассчитана выборочный коэффициент корреляции r=–0,227. Связь отрицательная, что соответствует теории (кривая Филлипса), но значима ли она? Проверить гипотезу H0:r=0 о равенстве нулю истинного значения коэффициента корреляции на уровне значимости a=0,05.
Решение. Вычисляем наблюдаемое и критическое значения критерия Стьюдента
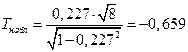 и
и 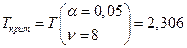 .
.
Поскольку 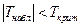 , то коэффициент корреляции не значимо отличается от нуля. Следовательно, в нашем случае не исключается, что истинное значение коэффициента корреляции равно нулю, т.е. на основе имеющейся выборки нельзя делать вывод о наличии корреляционной значимой линейной связи показателей инфляции и безработицы в США. Нельзя, впрочем, здесь делать вывод об отсутствии такой связи. â
, то коэффициент корреляции не значимо отличается от нуля. Следовательно, в нашем случае не исключается, что истинное значение коэффициента корреляции равно нулю, т.е. на основе имеющейся выборки нельзя делать вывод о наличии корреляционной значимой линейной связи показателей инфляции и безработицы в США. Нельзя, впрочем, здесь делать вывод об отсутствии такой связи. â
