Под определителем третьего порядка понимается выражение 3 страница

Решение. Построим график этих линий. 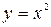- парабола, симметричная относительно оси 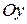. 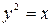- парабола, симметричная относительно оси .

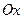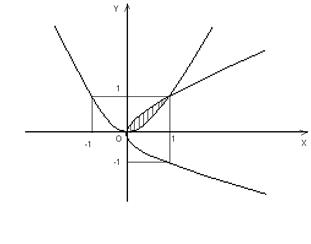
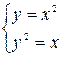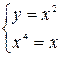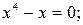
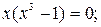
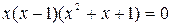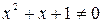
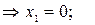
Найдем точки пересечения этих линий. Для этого решим систему , , ; 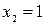. Искомая площадь равна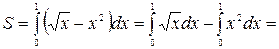

.

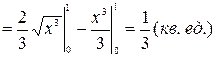Вопросы для самоподготовки.

1. Дайте определение первообразной функции.

2. Что называется неопределенным интегралом?

3. Сформулируйте основные свойства неопределенного интеграла.

4. Напишите таблицу простейших Н.И.

5. Укажите основные методы интегрирования.

6. Дайте определение интегральной суммы.

7. Что называется определенным интегралом?

8. Каков геометрический смысл определенного интеграла?

9. Сформулируйте основные свойства определенного интеграла.

10. Напишите формулу Ньютона – Лейбница.

11. Как вычисляется площадь плоской фигуры в прямоугольной системе координат?

Дифференциальные уравнения.

[1] гл. 7 §37-41, упр. 1-5, 32-36, 56-61 [2] Гл.22 §1-3, 7-9, 11-12 [3] гл. 8 §118-120

Уравнение вида 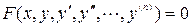(1), где 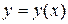- искомая функция, называется дифференциальным уравнением 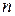-го порядка. Из определения видно, что порядок уравнения опреде­ляется наибольшим порядком, входящей в него производной.

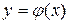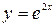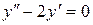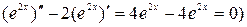Функция обращающая уравнение (1) в тождество, называется его решением (так функция есть решение уравнения ибо , а график этой функции - интегральной кривой.

Если решение 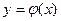задано в неявном виде 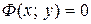, то его называют интегралом уравнения (1). Уравнение вида 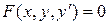(2) называют дифференциальным уравнением первого порядка.

Решив (2) относительно у', если это возможно, получим: 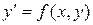. (3)

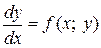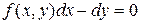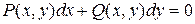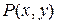Уравнение (3) часто записывают в виде или в виде , который является частным случаем общего уравнения , где и 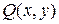- известные функции. (4)

Уравнение (3) имеет простой геометрический смысл: оно определяет наклон 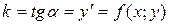интегральной кривой в точке .

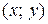Возникает вопрос, при каких условиях уравнение (3) имеет решение. Ответ на него дает теорема Коши:

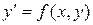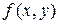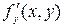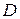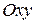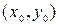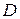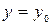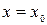Если в уравнении функция и ее частная производная определены и непрерывны в некоторой области плоскости , то какова бы ни была внутренняя точка области, существует единственное решение, удовлетворяю­щее условию при . (5)

Из теоремы Коши следует, что в области 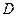уравнения (3) имеет бесконечное число различных решений.

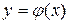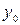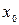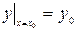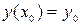Условия (5), в силу которых функция принимает заданное значение , в заданной точке , называются начальными условиями и записываются или . (6)

Нахождение решения уравнения (3) удовлетворяющего начальным условиям (6) называют задачей Коши. Общим решением уравнения (3) в не­которой области 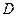называется функция 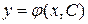, зависящая от 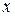и произвольной постоянной 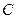, если:

а) она является решением уравнения (3) при любом значении постоянной

б) каковы бы ни были начальные условия (6) такие что 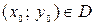, существует единственное значение постоянной 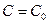такое, что функция 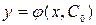удовлетворяет данным начальным условиям 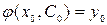. Любое решение уравнения (3), полученное из общего при определенном значении 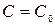называется частным решением.

Геометрически общее решение 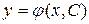есть семейство интегральных кривых на плоскости 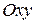, зависящее от одной произвольной постоянной 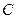, и частное решение 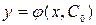- одну интегральную кривую этого семейства, проходящую через заданную точку .

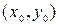Например, уравнение 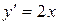удовлетворяет условиям теоремы Коши на всей плоскости 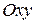( 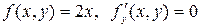- всюду определены и непрерывны), функция 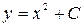- его общее решение, а функции 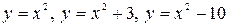- его частные решения, получающиеся соответственно при .

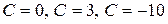Заметим, что для решения задачи Коши нужно начальные условия (6) подставить в общее решение уравнения (3) и найти значение 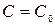. Так в нашем примере частным решением, удовлетворяющем начальному условию 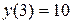, будет функция 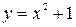, так как из равенства 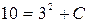следует .

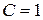Среди уравнений первого порядка особо важное значение имеет уравнение с разделяющимися переменными. Дифференциальное уравнение (4) называют уравнением с разделяющимися переменными, если функци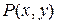и и 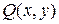можно представить в виде произведения двух функций, каждая из которых зависит только от 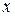или только от 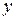, т.е. если оно имеет вид 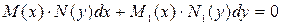. (7)

Разделив обе части уравнения (7) на 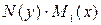получим: .

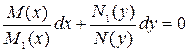Общий интеграл этого уравнения .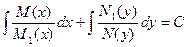

Пример. Найти частный интеграл (решение) дифференциального уравнения, удовлетворяющий заданному начальному условию: .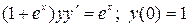

Решение. Это дифференциальное уравнение 1-го порядка с разделяющимися переменными. Найдем общий интеграл данного уравнения. Разделим обе части уравнения на 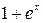. Получим: 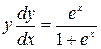; 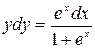. Интегрируя, находим 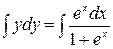; ; 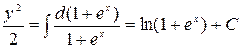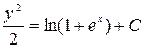- общий интеграл заданного уравнения. Подставляя сюда начальные условия, найдем постоянную С.

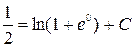или 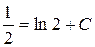, 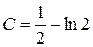. Тогда искомый частный интеграл будет иметь вид: 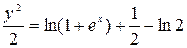или 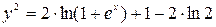. Окончательно: .

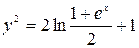Дифференциальное уравнение второго порядка имеет вид 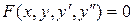. Разрешив его относительно 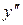(обычно изучают такие уравнения) получим 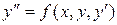. (9)

Теорема Коши, задача Коши, понятие общего и частного решений уравне­ния второго порядка формулируются аналогично этим понятиям для уравнения первого порядка.

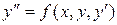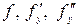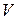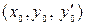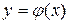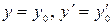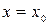Теорема Коши. Если в уравнении функции определены и непрерывны в некоторой области , то какова бы ни была внутренняя точка этой области, существует единственное решение данного уравнения, удовлетворяющее условиям при .(10)

Условия (10) называют начальными условиями и обычно записывают так 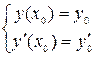(11)

Функцию 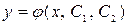называют общим решением уравнения (9) в области 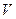, если она является решением (9) при любых значениях постоянных 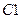и 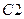, и если при любых начальных условиях (11) существуют единственные значения постоянных 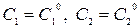такие, что функция 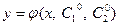удовлетворяет данным начальным условиям. Любая функция 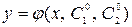, полученная из общего решения, называется частным решением.

Рассмотрим два частных вида уравнения (9). Уравнение вида 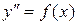решается последовательным 2-кратным интегрированием правой части. Действительно, его можно записать 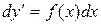тогда 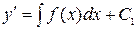, откуда 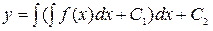. Это и есть общее решение.

Пример. Найти решение дифференциального уравнения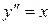 ,удовлетворяющее начальным условиям .

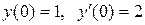Решение. Данное уравнение можно записать так 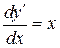или 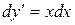. Интегрируя обе части, имеем: 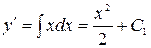. Откуда 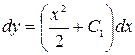. Интегрируя обе части еще раз, окончательно подучим 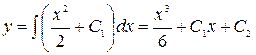. Найдем частное решение, удовлетворяющее заданная начальная условиям. Имеем: 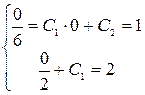, откуда .

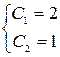Искомое частное решение будет .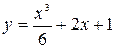

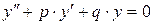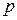Уравнение вида , где и 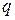числа, называется линейным однородным уравнением второго порядка с постоянными коэффициентами. Его частные решения обладают свойствами:

1. Есл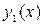и и 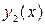частные решения, то функци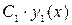и и 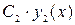также являются частными решениями;

2. Функция 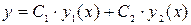также есть решение уравнения, причем, если 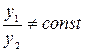, то она является его общим решением. Частные решения уравнения 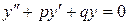отыскиваются в виде 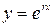,тогда ,

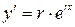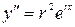
и мы имеем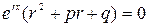 ,откуда 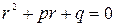. Это уравнение называют характеристическим. При его решении возможны случаи:

а) корни действительные и разные 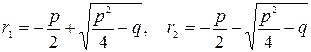. Получаем два частных решения 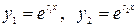, и так как 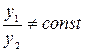, то общее решение запишется в виде .

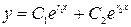б) корни действительные и равные 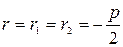, тогда 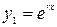. В качестве второго частного решения берут функцию 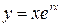, а общее решение имеет вид ,

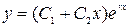в) корни комплексно-сопряженные 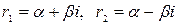, тогда частные решения 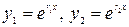и, так как 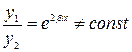, то общее решение имеет вид .

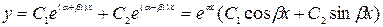Пример. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям: , , .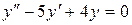

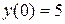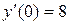Решение. Это однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Найдем общее решение его. Составим характеристическое уравнение и найдем его корни: .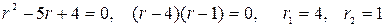

Так как корни характеристического уравнения действительные и различ­ные, то общее решение дифференциального уравнения будет иметь вид: 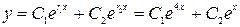. Найдем частное решение, удовлетворяющее начальным условиям. 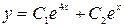, 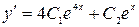. Подставим сюда начальные условия: 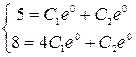или 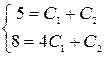. Вычитая из 2-го уравнения 1-е, получим 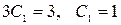. Тогда из первого уравнения получаем 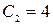. 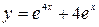- искомое частное решение.

Вопросы для самопроверки

1. Какое уравнение называется дифференциальным?

2. Дайте определение дифференциального уравнения первого порядка.

3. Дайте определение общего и частного решения (интеграла) для дифференциального уравнения первого порядка.

4. Сформулируйте задачу и теорему Коши для дифференциального уравнения первого порядка.

5. Что называется интегральной кривой?

6. Дайте геометрическое истолкование дифференциального уравнения первого порядка, выясните геометрический смысл общего и частного решений.

7. Дайте определение дифференциального уравнения с разделяющимися переменными. Какой вид имеет его общий интеграл? Приведите пример решения.

8. Сформулируйте теорему и задачу Коши для дифференциального уравнения второго порядка.

9. Дайте определение общего и частного решений дифференциального уравнения второго порядка.

10. Изложите метод решения дифференциального уравнения вида 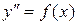. Приведите пример.

11. Дайте определение линейного однородного дифференциального уравнения второго порядка. Сформулируйте основные свойства его частных решений.

12. Какой вид имеет общее решение линейного однородного уравнения второ­го порядка?

13. Выведите формулу для общего решения линейного однородного уравнения второго порядка с постоянными коэффициентами в случае действитель­ных различных корней характеристического уравнения.

14. Сделайте также для случаев действительных равных и комплексных корней характеристического уравнения.

Ряды.

Литература. [2] ,гл.21,§1-13,упр. §19 3-5,7-9,13-15,17.18; [3] ,гл.14 §121-130

I. Знакопостоянные ряды

Выражение вида 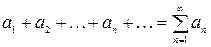, (1)

где все 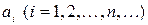имеют один и тот же знак, называется знакопостоянным числовым рядом, а 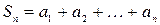- его 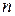- ой частичной суммой.

Ряд (1) называется сходящимся, если его частичная сумма 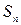имеет ко­нечный предел 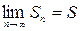. Число 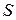при этом называют суммой ряда, а 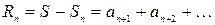- остатком ряда.

Если 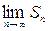не существует (или бесконечен), то ряд называют расходящимся. Так геометрический ряд 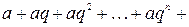при 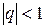сходится,

ибо его 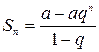и 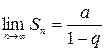, а гармонический ряд, т.е. ряд вида 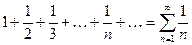расходится. Если ряд сходится, то 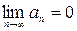(необходимый признак сходимости). Обратное утверждение местане имеет. Сходящиеся ряды обладают следующими свойствами:

1. Если сходится ряд (1), то сходится также ряд 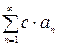, где с - любое постоянное;

2.Сумма (разность) двух сходящихся рядов есть ряд сходящийся.

3. Если сходится ряд (1), то сходится и любой его остаток и, наоборот из сходимости какого-нибудь остатка следует сходимость ряда. Рассмотрим достаточные признаки сходимости знакопостоянных рядов.

а) первый признак сравнения.

Пусть даны два ряда (1) и 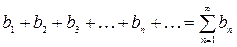. (2)

Если начиная с некоторого 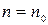, 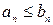и ряд (2) схо­дится, то ряд (1) также сходится; а если ряд (1) расходится то расхо­дится и ряд (2). Например, ряд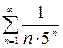сходится, так как при любом 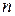справедливо неравенство 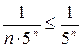, а геометрический ряд 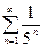сходится. Ряд же 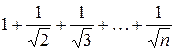расходится, ибо 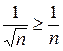, а гармонический ряд расходятся.

б) второй признак сравнения. Если существует конечный и неравный нулю предел 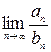, то ряды (1) и (2) сходятся или расходятся одно­временно.

Например, ряд 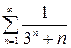сходится, так как здесь и, сравнивая его с геометрическим сходящимся рядо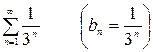м имеем 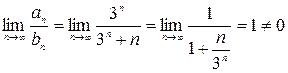. Ряд же 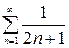расходится, так как 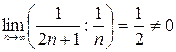, а гармонический ряд 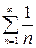- расходится.

в) признак Даламбера. Пусть дан ряд 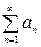. Если существует ,

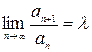то при 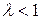ряд сходится; при 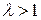- расходится. При 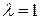признак не применим.

Пример. Исследовать сходимость числовых рядов: а) 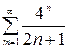, б) 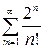.