Под определителем третьего порядка понимается выражение 2 страница
11. 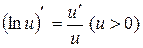
Здесь 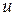 и
и 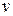 дифференцируемые функции от
дифференцируемые функции от 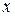 , а
, а 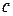 – постоянная.
– постоянная.
Геометрический смысл производной
Производная функция 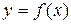 представляет собой угловой коэффициент касательной, проведенной к графику функции в любой ее точке.
представляет собой угловой коэффициент касательной, проведенной к графику функции в любой ее точке.
Уравнение касательной, проведенной к графику функции 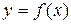 в точке
в точке 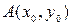 имеет вид
имеет вид 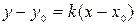 , где
, где 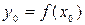 ,
, 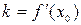 .
.
Физический смысл производной. Если тело движется прямолинейно по закону 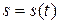 , то производная пути
, то производная пути 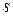 по времени
по времени 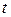 равна скорости движения тела в данный момент времени
равна скорости движения тела в данный момент времени 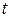 :
: 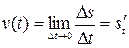 .
.
Производной второго порядка функции 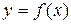 называется производная от первой производной, т.е.
называется производная от первой производной, т.е. 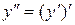 .
.
Физический смысл второй производной. Если тело движется прямолинейно по закону 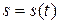 , то вторая производная пути
, то вторая производная пути 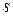 по времени
по времени 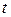 равна ускорению движения тела в данный момент времени
равна ускорению движения тела в данный момент времени 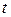 :
: 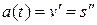 .
.
Пример. Найти производные функций:
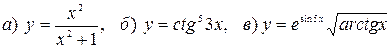 .
.
Решение. а) дифференцируем функцию по формуле 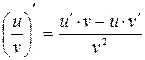 ,
,
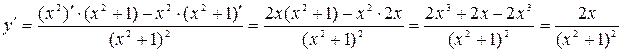 .
.
б) воспользуемся формулой дифференцирования сложной функции: 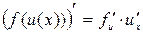 , получим
, получим 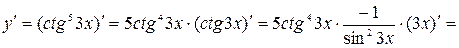
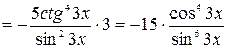 .
.
в) 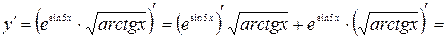
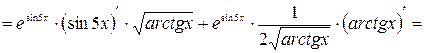
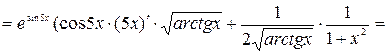
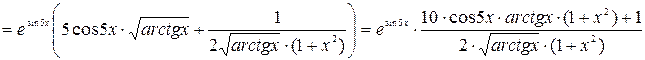 .
.
Вопросы и упражнения для самопроверки.
1. Дайте определение производной.
2. Запишите формулы производной произведения, частного.
3. В чем состоит геометрический смысл производной?
4. Как найти скорость движения тела, если задан закон прямолинейного движения?
5. Запишите уравнение касательной к кривой 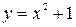 в точке
в точке 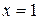 .
.
6. В чем состоит физический смысл второй производной?
7. Запишите формулу производной сложной функции.
8. Найдите 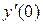 , если
, если 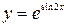 .
.
Приложения производной к исследованию функций.
Литература. [1] гл. 3 § 18,19, [2] гл. 11 § 1,2, 7-10, [3] гл. 9 §86-96.
Дифференцируемая функция 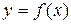 возрастает на промежутке
возрастает на промежутке 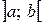 , если ее производная положительна в каждой точке этого промежутка.
, если ее производная положительна в каждой точке этого промежутка.
Дифференцируемая функция 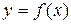 убывает на промежутке
убывает на промежутке 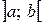 , если ее производная отрицательна в каждой точке этого промежутка.
, если ее производная отрицательна в каждой точке этого промежутка.
Функция 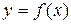 имеет в точке
имеет в точке 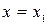 максимум, если для всех
максимум, если для всех 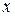 , достаточно близких к
, достаточно близких к 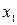 , выполняется неравенство
, выполняется неравенство 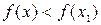 .
.
Функция 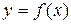 имеет в точке
имеет в точке 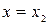 минимум, если для всех значений
минимум, если для всех значений 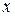 достаточно близких к
достаточно близких к 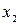 , выполняется неравенство
, выполняется неравенство 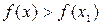 . Точки максимума и минимума называются точками экстремума.
. Точки максимума и минимума называются точками экстремума.
Необходимое условие экстремума функции.
Если в точке 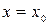 дифференцируемая функция имеет экстремум, то в этой точке
дифференцируемая функция имеет экстремум, то в этой точке 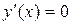 . Точки в которых
. Точки в которых 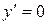 называются критическими.
называются критическими.
Первое достаточное условие существования экстремума функций. Если при перехода через критическую точку 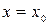 производная меняет знак, то
производная меняет знак, то 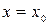 точка экстремума. При этом если производная меняет знак с плюса на минус, то
точка экстремума. При этом если производная меняет знак с плюса на минус, то 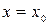 точка максимума, а
точка максимума, а 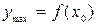 . Если же производная меняет знак с минуса на плюс, то
. Если же производная меняет знак с минуса на плюс, то 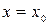 точка минимума, а
точка минимума, а 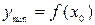 .
.
Говорят, что на промежутке 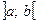 кривая обращена выпуклостью вверх, или выпукла, если она лежит ниже касательной, проведенной в любой ее точке.
кривая обращена выпуклостью вверх, или выпукла, если она лежит ниже касательной, проведенной в любой ее точке.
Говорят, что кривая на промежутке 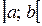 обращена выпуклостью вниз или вогнута, если она лежит выше касательной, проведенной в любой ее точке.
обращена выпуклостью вниз или вогнута, если она лежит выше касательной, проведенной в любой ее точке.
Точка, в которой меняется направление вогнутости кривой, называется точкой перегиба.
График дифференцируемой функции 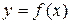 является вогнутым на промежутке
является вогнутым на промежутке 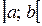 , если вторая производная функции положительна в каждой точке этого промежутка.
, если вторая производная функции положительна в каждой точке этого промежутка.
График дифференцируемой функции 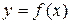 является выпуклым на промежутке
является выпуклым на промежутке 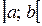 , если вторая производная функции отрицательна в каждой точке этого промежутка.
, если вторая производная функции отрицательна в каждой точке этого промежутка.
Необходимым условием точки перегиба дифференцируемой функции является равенство нулю второй производной, а достаточным условием является то, что при переходе через эту точку 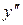 меняет знак.
меняет знак.
Прямая 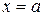 является вертикальной асимптотой, если
является вертикальной асимптотой, если 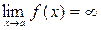 . Уравнение наклонной асимптоты имеет вид
. Уравнение наклонной асимптоты имеет вид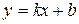 ,где
,где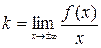 ,
, 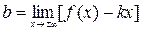 ,при условии, что оба эти предела существуют.
,при условии, что оба эти предела существуют.
Исследование функции в построение графиков можно проводить по следующей схеме:
1. Найти область определения функции.
2. Установить нечетность, четность и периодичность функции.
3. Найти точки разрыва.
4. Найти асимптоты.
5. Найти промежутки монотонности и экстремумы функции.
6. Найти направление вогнутости и точки перегиба.
7. Найти точки пересечения графика функции с осями координат и при необходимости, несколько дополнительных точек.
8. Построить график, используя результаты исследования.
Пример. Исследовать функцию 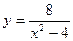 и построить ее график.
и построить ее график.
Решение. Функция определена для всех значений 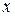 , кроме
, кроме 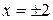 .
. 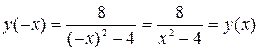 , следовательно, функция четная и график ее будет симметричен относительно оси
, следовательно, функция четная и график ее будет симметричен относительно оси 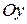 .
. 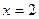 и
и 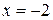 - вертикальные асимптоты.
- вертикальные асимптоты.
Найдем наклонные асимптоты 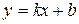 .
. 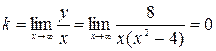 ,
, 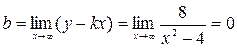 . Таким образом, прямая
. Таким образом, прямая 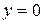 является горизонтальной асимптотой. Найдем интервалы возрастания, убывания функции и точки экстремума.
является горизонтальной асимптотой. Найдем интервалы возрастания, убывания функции и точки экстремума. 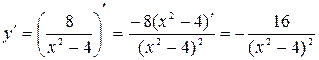 . Находим критические точки, где
. Находим критические точки, где 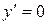 .
. 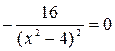 ;
; 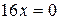 ;
; 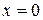 . Производная
. Производная 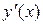 не определена при
не определена при 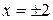 . Область определения функции разбивается на четыре участка монотонности.
. Область определения функции разбивается на четыре участка монотонности.
При 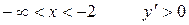 , следовательно, функция возрастает.
, следовательно, функция возрастает.
При 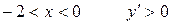 , следовательно, функция возрастает.
, следовательно, функция возрастает.
При  - функция убывает.
- функция убывает.
При  - функция убывает.
- функция убывает.
При переходе через точку 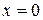
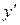 меняет знак с
меняет знак с 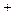 на -, следовательно,
на -, следовательно, 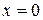 будет точкой максимума.
будет точкой максимума. 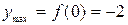 .
.
Найдем интервалы выпуклости, вогнутости и точки перегиба. 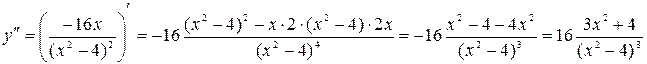 .
.
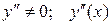 не существует при
не существует при 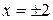 .
.
При 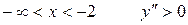 , следовательно, график вогнутый.
, следовательно, график вогнутый.
При 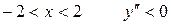 следовательно, на этом интервале график выпуклый.
следовательно, на этом интервале график выпуклый.
При 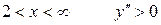 следовательно, график вогнутый.
следовательно, график вогнутый.
Точек перегиба график не имеет. Построим график.
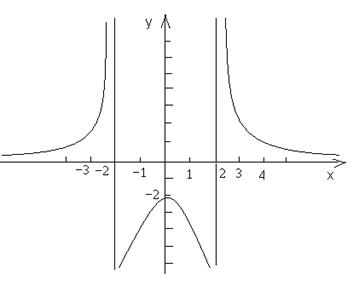
Вопросы и упражнения для самопроверки.
1. Сформулируйте необходимые условия экстремума функции.
2. Как найти промежутки возрастания и убывания функции?
3. В чем состоит достаточное условие экстремума?
4. Как найти промежутки выпуклости и вогнутости кривой?
5. Как найти точки перегиба кривой?
6. Найдите точки экстремума функции: 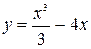
Неопределенный интеграл.
Литература. [1] гл. 4 §20, 21, 28 упр1-89 [2] гл.11 §102-104 [3] гл. 13 §1-5, 10, упр. 1-32.
Как известно основная задача дифференциального исчисления сводится к нахождению по заданной функции ее производной. Неопределенный интеграл решает обратную задачу: по заданной производной находят первоначальную функцию.
Функцию 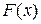 называют первообразной для функции
называют первообразной для функции 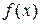 в интервале
в интервале 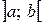 , если
, если 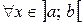 имеет место равенство
имеет место равенство 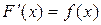 . Так для функции
. Так для функции 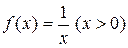 первообразной служит функция
первообразной служит функция 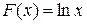 , так как для любого
, так как для любого 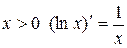 ; для функции
; для функции 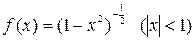 первообразной является функция
первообразной является функция 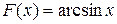 поскольку
поскольку 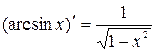
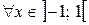 и т.д.
и т.д.
Если 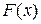 -первообразная для функции
-первообразная для функции 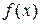 , то множество функций
, то множество функций 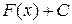 , где
, где 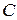 - произвольная постоянная, называют неопределенным интегралом от функции
- произвольная постоянная, называют неопределенным интегралом от функции 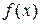 и обозначают символом
и обозначают символом 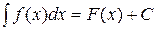 .
.
Например, 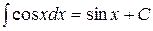 , так как
, так как 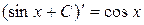 .
.
Приведем основные свойства неопределенных интегралов (Н.И.).
1. Производная от Н.И. равна подынтегральной функции, а дифференциал -подынтегральному выражению, т.е. 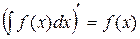
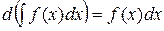 .
.
2. Н.И. от дифференциала функции равен этой функции плюс произвольное постоянное, т.е. 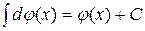 .
.
3. Постоянный множитель можно выносить за знак Н.И.: 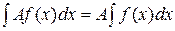
4. Н.И.от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов: 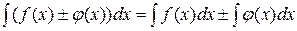 .
.
Таблица простейших интегралов имеет вид:
1. 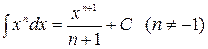 2.
2. 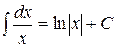
3. 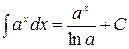 4.
4. 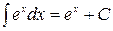
5. 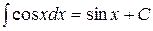 6.
6. 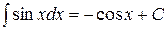
7. 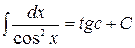 8.
8. 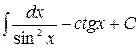
9. 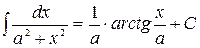 10.
10. 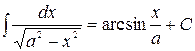
11. 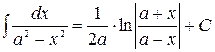
Основными методами интегрирования являются: разложения, подстановки, по частям. Интегрирование методом разложения заключается в приведении данного интеграла (по свойству 4) к сумме более простых или табличных интегралов. Метод подстановки имеет в виду следующее: положив в интеграле 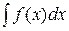
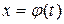 ,
, 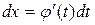 получим
получим 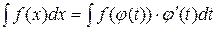 . При интегрировании по частям берут формулу дифференциала произведения:
. При интегрировании по частям берут формулу дифференциала произведения: 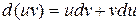 и из нее после интегрирования обеих частей получают формулу
и из нее после интегрирования обеих частей получают формулу 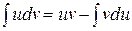 . Эта формула применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функций, например:
. Эта формула применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функций, например: 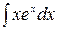 или
или 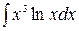 .
.
При этом за 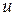 принимают функцию, которая дифференцированием упрощается, а за
принимают функцию, которая дифференцированием упрощается, а за 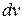 та часть подынтегрального выражения содержащая
та часть подынтегрального выражения содержащая 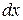 , интеграл от которой известен или может быть найден. Например, в интеграле
, интеграл от которой известен или может быть найден. Например, в интеграле 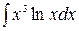 за
за 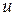 нужно принять
нужно принять 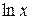 , а в интеграле
, а в интеграле 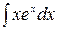 положить
положить 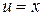 .
.
Пример. Найти неопределенные интегралы:
а) 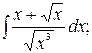 б)
б) 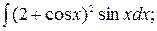 в)
в) 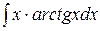 .
.
Решение.
а) 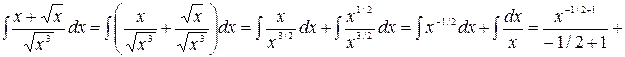
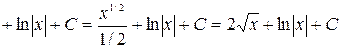 .
.
б) применим метод подстановки. Положим 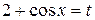 ; тогда
; тогда 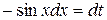 , откуда
, откуда 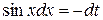 .
.
Получаем 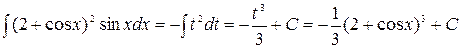 .
.
в) применим формулу интегрирования по частям. Обозначим 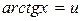 ,
, 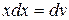 , тогда
, тогда 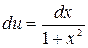 ,
, 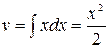 .
.
Получаем 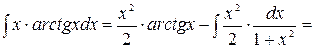
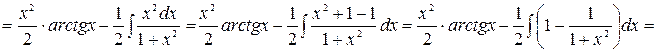
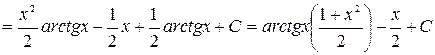 .
.
Определенный интеграл.
Литература. [1] §23, 24, 26, 28, упр 108-113, 116-125,150-152. [2] гл. 14 §1-9
Пусть на отрезке 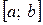 определена функция
определена функция 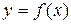 . Разобьем отрезок
. Разобьем отрезок 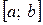 на
на 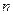 произвольных частей точками
произвольных частей точками 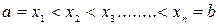 . На каждом отрезке
. На каждом отрезке 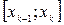 возьмем произвольную точку
возьмем произвольную точку 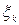 , вычислим значение функции в этой точке
, вычислим значение функции в этой точке 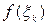 и составим сумму:
и составим сумму: 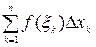 , где
, где 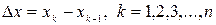 . Эту сумму называют интегральной суммой функции
. Эту сумму называют интегральной суммой функции 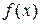 по отрезку
по отрезку 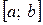 . Предел суммы
. Предел суммы 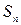 при условии, что длина наибольшего из отрезков
при условии, что длина наибольшего из отрезков 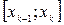 стремится к нулю
стремится к нулю 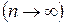 , если он существует, и не зависит ни от способа разбиения, ни от способа выбора точек
, если он существует, и не зависит ни от способа разбиения, ни от способа выбора точек 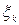 , называется определенным интегралом функции
, называется определенным интегралом функции 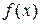 в пределах от
в пределах от 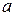 до
до 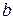 и обозначается
и обозначается 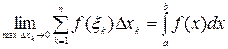 . Функцию
. Функцию 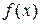 в этом случае называют интегрируемой на отрезке
в этом случае называют интегрируемой на отрезке 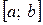 . Всякая ограниченная на отрезке
. Всякая ограниченная на отрезке 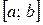 функция, имеющая лишь конечное число точек разрыва, интегрируема.
функция, имеющая лишь конечное число точек разрыва, интегрируема.
В частности интегрируема любая непрерывная на отрезке 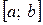 функция, так как в этом случае для нее существует Н.И.
функция, так как в этом случае для нее существует Н.И. 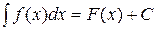 и имеет место формула
и имеет место формула 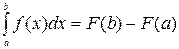 , которая называется формулой Ньютона – Лейбница.
, которая называется формулой Ньютона – Лейбница.
Если непрерывная кривая задана уравнением 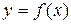
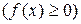 , то площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми 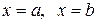 и отрезком
и отрезком 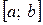 определяется формулой
определяется формулой 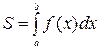 . В общем случае, если площадь ограничена двумя кривыми
. В общем случае, если площадь ограничена двумя кривыми 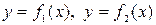 , где
, где 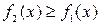 , двумя прямыми
, двумя прямыми 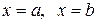 и отрезком
и отрезком 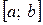 имеет место формула
имеет место формула 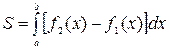 .
.
Пример. Вычислить интегралы а) 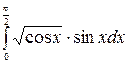 . б)
. б) 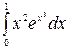 .
.
Решение.
а) произведем подстановку 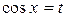 ; тогда
; тогда 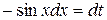 . Определим пределы для переменной
. Определим пределы для переменной 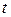 .
. 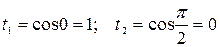 .
.
Тогда 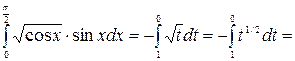
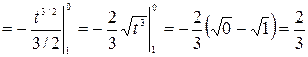 .
.
б) положим 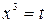 , тогда
, тогда 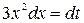 ,
, 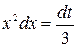 . Определим пределы интегрирования для переменной
. Определим пределы интегрирования для переменной 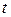 :
: 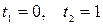 . Тогда
. Тогда 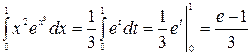 .
.
Пример. Вычислить площадь фигуры, ограниченной линиями 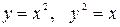 .
.
