Под определителем третьего порядка понимается выражение 4 страница

Решение. Для исследования сходимости данного ряда воспользуемся

признаком Даламбера. Найдем . ; ;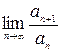

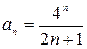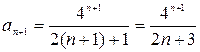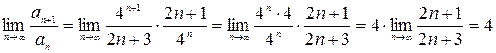
Так как 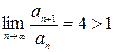, то заданный ряд расходится.

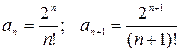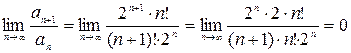б) Так как и - данный ряд сходится.

г) радикальный признак Коши. Если для ряда (1) существует 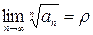, то при 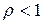ряд сходится; при 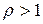- расходится; при 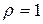признак не применим.

Например, ряд 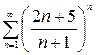расходятся, так как 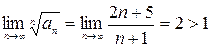, а ряд 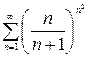сходится в силу того, что .

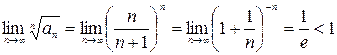2.Знакопеременные ряды.

Под такими рядами понимаются ряды, члены которых имеют произвольные знаки. Ряд вида 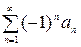(3) называется знакочередующимся. Достаточный признак сходимости такого ряда (признак Лейбница) формулируется так: если члены ряда (3), взятые по модулю монотонно убывают и общий член стремится к нулю, то ряд сходится. Имеет также место следующий достаточный признак сходимости знакопеременного ряда: пусть дан знакопеременный ряд 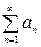, тогда, если сходится ряд

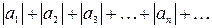(4)

составленный из модулей его членов, то сходится и сам ряд.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд (4). Сходящийся знакопеременный ряд называют условно сходящимся, если ряд (4) расходится.

Пример. Исследовать на сходимость ряды:

а) ;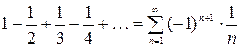

б) .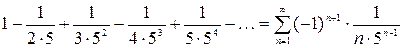

Решение а) так как члены ряда взятые по модулю убывают и 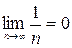, то ряд сходится условно, в силу того что ряд из модулей расходится.

б) так как ряд, составленный из модулей членов данного ряда

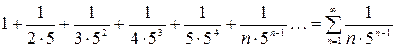сходится, то сам ряд сходится абсолютно. Заметим, что абсолютно сходящиеся ряды обладают свойствами конечных сумм, что не имеет места для условно сходящегося ряда.

З. Функциональные ряды

Ряд вида 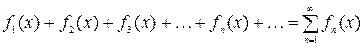(5)

называется функциональным рядом. Совокупность значений 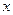, при которых ряд (5) сходится, называется его областью сходимости.

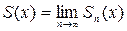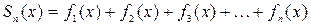Функция , где , а 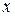принадлежит области сходимости, называется суммой ряда, а разность 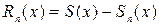- остатком ряда (5). Говорят, что ряд (5) сходится равномерно и абсолютно на отрезке 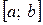, если существует числовой знакоположительный сходящийся ряд 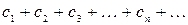такой, что при любом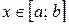 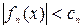. Равномерно сходящиеся ряды обладают рядом свойств, аналогичных свойствам многочленов:

а) если члены ряда(5) непрерывны на отрезке 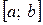и он сходится равномерно, то его сумма 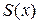также непрерывна на отрезке ;

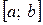б) равномерно сходящийся ряд непрерывных функций можно почленно интегрировать и дифференцировать.

Важным частным случаем функциональных рядов являются степенные ряды, так называются ряды вида 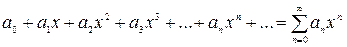(6)

(в общем случае ряды вида ).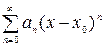

Имеет место следующая теорема Абеля.

Если ряд (6) сходится при 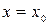, то он абсолютно сходится для всех 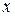, удовлетворяющих неравенству, 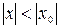, а если при 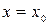он расходится, то он будет расходиться и при всех 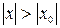. Другими словами, из сходимости ряда (6) в точке 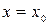,вытекает его сходимость в интервале 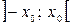, а из расходимости в точке 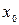, следует расходимость в интервалах 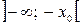и 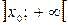. Отметим также, что ряд (6) сходится равномерно в любом промежутке 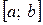, целиком содержащемся внутри его интервала сходимости (вторая теорема Абеля).

Радиус сходимости степенного ряда вычисляется по формуле .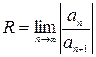

Если 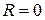, то ряд сходится только в одной точке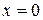, если 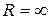, то он сходится на всей числовой прямой, а если 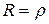, то он сходится в интервале 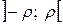и расходится вне этого интервала. Сходимость в точках 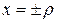выясняется отдельно.

Пример. Определять интервал сходимости рядов а) 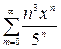; б)

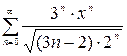
Решение: а) здесь 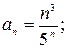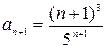, следовательно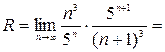

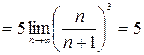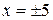. При имеем ряды: 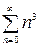; 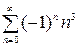, которые расходятся, т.к. не выполняется необходимый признак сходимости. Итак, данный ряд сходится для всех .

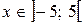б) имеем 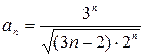, 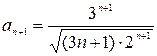. Радиус сходимости

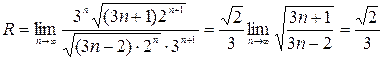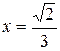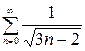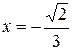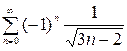. При имеем ряд , который расходится по признаку сравнения. При ряд сходится условно.

Таким образом, данный ряд сходится для .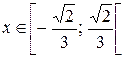

Если функция 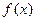в некоторой окрестности точки 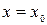имеет производные всех порядков, которые в совокупности ограничены (существует число 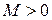, такое, что 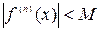), то она в этой окрестности может быть представлена единственным образом в виде степенного ряда:

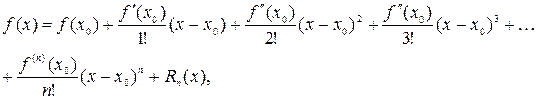
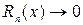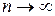где при , который называется рядом Тейлора.

Если 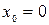, то ряд Тейлора имеет вид:

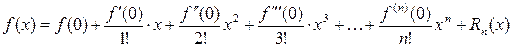и называется рядом Маклорена. Имеют место следующие основные разложения:

;

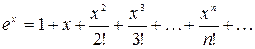
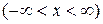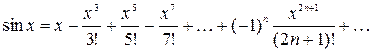
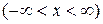
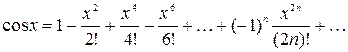
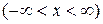
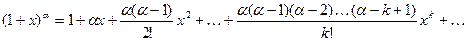
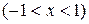
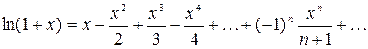
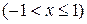
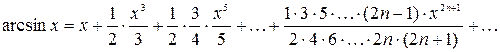
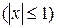
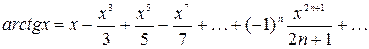
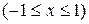
Используя основные разложения и свойства степенных рядов, можно представить в виде ряда и другие элементарные функции.

Пример. Пользуясь разложением в стеленной ряд функции 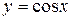записать разложение в ряд функции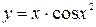

Решение.

Запишем разложение в ряд функции :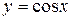

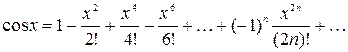. Положив вместо 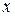всюду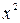 ,получим разложение для :

.

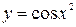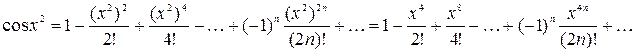Умножая левую и правую части равенства на 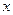, получим искомое разложение:

.

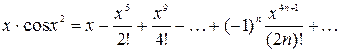Вопросы для самоподготовки.

1. Дайте определение числового ряда.

2. Что называется частичной суммой ряда?

3. Какой ряд называется сходящимся, расходящимся?

4. Сформулируйте необходимый признак сходимости числового ряда.

5. Сформулируйте основные свойства сходящихся рядов.

6. Перечислите известные вам достаточные признаки сходимости знакопостоянных рядов.

7. Сформулируйте первый и второй признаки сравнения знакоположитель­ных рядов. Приведите пример этих признаков.

8. Сформулируйте признак Даламбера сходимости знакопостоянных рядов. Приведите пример применения этого признака.

9. Дайте формулировку радикального признака Коши. Приведите пример применения этого признака.

10. Можно ли решать вопрос о сходимости ряда не пользуясь необходи­мым признаком сходимости?

11. Дайте формулировку признака Лейбница. Приведите пример применения этого признака.

12. Дайте определение абсолютно (условно) сходящегося ряда.

13. Сформулируйте основной достаточный признак сходимостизнакопеременных рядов.

14. Какой ряд называется функциональным?

15. Дайте определение области сходимости функционального ряда. Приведите примеры её нахождения.

16. Дайте определение равномерно сходящегося ряда.

17. Сформулируйте основные свойства равномерно сходящихся рядов.

18. Какой ряд называется степенным?

19. Сформулируйте первую теорему Абеля. Приведите пример ее при­менения.

20. Сформулируйте вторую теорему Абеля.

21. Напишите формулу для нахождения радиуса сходимости степенного ряда.

22. В чём заключаются условия разложимости функции в ряд Тейлора?

23. Напишите разложения в ряд Маклорена для основных элементарных функций.

Баранова И.М., доцент

Буров П.А., доцент,

Муравьев А. Н, доцент

Математика

Конспект лекций

для студентов заочного обучения направления

«Лесное дело» и «Ландшафтная архитектура»

Объем 1,5 п.л. Тираж 30 экз. Заказ _______

Брянская государственная инженерно-технологическая академия