Тема 2 Метод сценариев и value at risk
Самостоятельная работа по дисциплине «Оценка рисков»
Тема 1: Количественная (расчетная) оценка и отсеиваниенекоторых экспертов. Метод экспертных оценок.
Простейший подход к процедуре основан на оценке близости мнения эксперта к среднему мнению группы. В случае большого расхождения кандидат «бракуется». Ниже представлена методика расчетной оценки качества экспертов [4].
Исходные данные: зачетное число специалистов-экспертов, из которых формируется экспертная группа – n, число ранжируемых факторов рисковой ситуации – k.
1) Каждому i-тому эксперту (i = 1, 2, … , n) предлагается проранжировать все расчетные факторы, влияющие на ситуацию, для которой в дальнейшем будет проводиться экспертная оценка рисков, то есть предлагается установить αij -ранг j-того фактора, j = 1, 2, … , k.
В результате получается матрица-строка мнений каждого i-того эксперта относительно значимости всех факторов (по отдельности для каждого фактора):

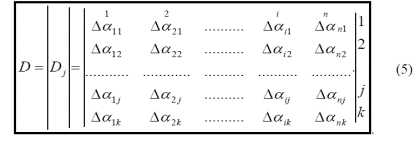

Пример решения задачи
Руководство компании приняло решение о привлечении группы внешних экспертов для анализа рисков не выполнения плана продаж. Допустим (условно), что по результатам отбора кандидатов в эксперты качественным методом было выбрано четыре эксперта с одинаковыми или очень близкими параметрами соответствия заявленным критериям отбора. Зачетная численность экспертной группы: четыре человека.
Итак, четырем кандидатам (n=4) было предложено проранжировать 6 критериев (к=6) выбора компании:
g1 – утрата оборудования;
g2 – невозможность поддержания запланированных цен;
g3 – опыт компании в производстве продукта;
g4 – репутация на рынке организации;
g5 – объем выполненных работ за предыдущий год;
g6 – текущее финансовое состояние организации.
Наиболее важному критерию присваивается 1-й ранг, наименее важному 6-й.
Общая матрица ранжирования имеет следующий вид:
| i | j | |||||
| G1 | G2 | G3 | G4 | G5 | G6 | |
| Σ | ||||||
| Ср. Знач Σ/4 | 1,5 | 2,25 | 2,5 | 5,5 | 5,25 |
Матрица отклонений мнений экспертов от среднего мнения:
| I | j | Ср/знач. Σ/6 | |||||
| G1 | G2 | G3 | G4 | G5 | G6 | ||
| |1 – 1,5| | |2 – 2,25| | |1 – 2,5| | |4-4| | |5-5,5| | |6-5,25| | 0,42 | |
| |2 – 1,5| | |1 -2,25| | |4-2,5| | |3-4| | |6-5,5| | |5-5,25| | 0,83 | |
| |1 – 1,5| | |3 – 2,25| | |2- 2,5| | |1-4| | |6-5,5| | |4-5,25| | 0,75 | |
| |2 – 1,5| | |3 – 2,25| | |1-2,5| | |4-4| | |5-5,5| | |6-5,25| | 0,67 |
Суммарное отклонение мнений всех экспертов по всем критериям:
Δā = 0,42+0,83+0,75+0,67 = 2,67
Среднее отклонение мнений i-того эксперта от среднего мнения группы по всем
критериям:
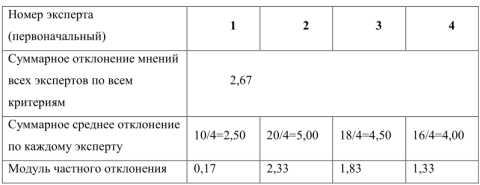
Отсюда следует, что эксперт №2 , может быть исключен из состава экспертной группы, так как его мнения наиболее удалены от среднего мнения.
Задача по вариантам
Руководство компании приняло решение о привлечении группы внешних экспертов для анализа рисков не выполнения плана продаж. Допустим (условно), что по результатам отбора кандидатов в эксперты качественным методом было выбрано четыре эксперта с одинаковыми или очень близкими параметрами соответствия заявленным критериям отбора. Зачетная численность экспертной группы: четыре человека.
Итак, четырем кандидатам (n=4) было предложено проранжировать 6 критериев (к=6) выбора компании:
g1 – утрата оборудования;
g2 – невозможность поддержания запланированных цен;
g3 – опыт компании в производстве продукта;
g4 – репутация на рынке организации;
g5 – объем выполненных работ за предыдущий год;
g6 – текущее финансовое состояние организации.
Наиболее важному критерию присваивается 1-й ранг, наименее важному 6-й.
Общая матрица ранжирования имеет следующий вид:
Таблица 1- Исходные данные
| i | j | i | j | i | j | |||||||||||||||
| Вариант1 | Вариант 2 | Вариант 3 | ||||||||||||||||||
| G1 | G2 | G3 | G4 | G5 | G6 | G1 | G2 | G3 | G4 | G5 | G6 | G1 | G2 | G3 | G4 | G5 | G6 | |||
| i | j | i | j | i | j | |||||||||||||||
| Вариант 4 | Вариант 5 | Вариант 6 | ||||||||||||||||||
| G1 | G2 | G3 | G4 | G5 | G6 | G1 | G2 | G3 | G4 | G5 | G6 | G1 | G2 | G3 | G4 | G5 | G6 | |||
| i | j | i | j | i | j | |||||||||||||||
| Вариант 7 | Вариант 8 | Вариант 9 | ||||||||||||||||||
| G1 | G2 | G3 | G4 | G5 | G6 | G1 | G2 | G3 | G4 | G5 | G6 | G1 | G2 | G3 | G4 | G5 | G6 | |||
| i | j | |||||||||||||||||||
| Вариант 10 | ||||||||||||||||||||
| G1 | G2 | G3 | G4 | G5 | G6 | |||||||||||||||
Тема 2 Метод сценариев и value at risk
VaR - это показатель риска, который показывает, какую максимальную сумму денег может потерять портфель инвестора в течение определенного периода времени с заданной доверительной вероятностью. Соответственно VaR также говорит о том, что потери в стоимости портфеля в течение этого периода времени будут меньше данной величины с определенной вероятностью. Доверительную вероятность можно определить как показатель, говорящий о том, какое количество раз из каждых 100 раз потери в стоимости портфеля не превысят данного уровня. Поэтому VaR призван ответить на следующий вопрос: "Какой может оказаться максимальная потеря в стоимости портфеля, например, в 95% случаев в течение следующего дня?" Уровень доверительной вероятности задается заранее и зависит от характера компании, владеющей портфелем, и от субъективного подхода управляющего портфелем к этому вопросу. Обычно он равен 95% или 99%. Следует подчеркнуть, что выбор того или иного уровня доверительной вероятности не говорит об отношении инвестора к риску, так как VaR - это только определенная точка в распределении ожидаемых результатов доходности портфеля.
Метод сценариев. Сценарный анализ (scenario analysis) - это иной метод анализа рисков, по мнению многих, более корректно отражающий реальность.
В соответствии со сложившимся убеждением анализ чувствительности неверно отражает фактическую ситуацию, поскольку основан на предположении, что изменение одного параметра финансовой модели происходит независимо от остальных, а это не так. Например, рост объемов продаж сопровождается ростом затрат, налогов и т.п., и изменению подвергаются сразу несколько параметров.
При осуществлении сценарного анализа формулируются допущения и рассчитывается бюджет денежных потоков не для одного, а для трех-пяти возможных сценариев развития событий. При этом при изменении сценария могут измениться все параметры финансовой модели. Во-первых, такой подход дает возможность развернуто охарактеризовать потенциальные выгоды и убытки проекта (сопоставить по масштабу возможные выгоды с вероятными потерями). Во-вторых, он позволяет дать вероятностную характеристику проекту в целом.
Вероятностные характеристики проекта. Для расчета вероятностных характеристик проекта каждому из сценариев присваивается своя вероятность реализации (Pj). Затем рассчитываются интегральные характеристики проекта:
математическое ожидание (NPV): Е (NPV) = ΣPi * NPVi, (12)
где NPV j - чистая приведенная ценность для j-ro сценария; Р – вероятность возникновения сценария
 σ стандартное отклонение NPV: σ = √̅ΣРi * (NPVi – E(NPV))2 (13)
σ стандартное отклонение NPV: σ = √̅ΣРi * (NPVi – E(NPV))2 (13)
VaR = E(NPV) ± zσ
Задача 1
Для проекта " Novell" разработаны пять сценариев дальнейшего развития событий
Таблица 2 – Сценарии развития проекта
| Сценарии | NPVi (млн.руб) | Pi | Сценарии | NPVi (млн.руб) | Pi |
| Вариант 1 | Вариант 2 | ||||
| Оптимистический | 52,1 | 0.1 | Оптимистический | 40,3 | 0.2 |
| Умеренно-оптимистический | 32,1 | 0.2 | Умеренно-оптимистический | 30,1 | 0.1 |
| Наиболее вероятный | 24,3 | 0.3 | Наиболее вероятный | 21,5 | 0.4 |
| Умеренно - пессимистический | 11,5 | 0.2 | Умеренно - пессимистический | 10,2 | 0.2 |
| Пессимистический | -8,5 | 0.2 | Пессимистический | -5,5 | 0.1 |
| Сценарии | NPVi (млн.руб) | Pi | Сценарии | NPVi (млн.руб) | Pi |
| Вариант 3 | Вариант 4 | ||||
| Оптимистический | 42,1 | 0.1 | Оптимистический | 47,3 | 0.2 |
| Умеренно-оптимистический | 22,1 | 0.2 | Умеренно-оптимистический | 32,1 | 0.1 |
| Наиболее вероятный | 14,3 | 0.3 | Наиболее вероятный | 25,5 | 0.4 |
| Умеренно - пессимистический | 10,5 | 0.2 | Умеренно - пессимистический | 13,2 | 0.2 |
| Пессимистический | -5,5 | 0.2 | Пессимистический | -6,5 | 0.1 |
| Сценарии | NPVi (млн.руб) | Pi | Сценарии | NPVi (млн.руб) | Pi |
| Вариант 5 | Вариант 6 | ||||
| Оптимистический | 50,1 | 0.1 | Оптимистический | 48,3 | 0.2 |
| Умеренно-оптимистический | 37,1 | 0.2 | Умеренно-оптимистический | 36,1 | 0.1 |
| Наиболее вероятный | 29,3 | 0.3 | Наиболее вероятный | 23,5 | 0.4 |
| Умеренно - пессимистический | 18,5 | 0.2 | Умеренно - пессимистический | 14,2 | 0.2 |
| Пессимистический | -9,5 | 0.2 | Пессимистический | -8,5 | 0.1 |
| Сценарии | NPVi (млн.руб) | Pi | Сценарии | NPVi (млн.руб) | Pi |
| Вариант 7 | Вариант 8 | ||||
| Оптимистический | 56,1 | 0.1 | Оптимистический | 52,3 | 0.2 |
| Умеренно-оптимистический | 40,1 | 0.2 | Умеренно-оптимистический | 39,1 | 0.1 |
| Наиболее вероятный | 27,3 | 0.3 | Наиболее вероятный | 29,5 | 0.4 |
| Умеренно - пессимистический | 15,5 | 0.2 | Умеренно - пессимистический | 15,2 | 0.2 |
| Пессимистический | -9,5 | 0.2 | Пессимистический | -7,5 | 0.1 |
| Сценарии | NPVi (млн.руб) | Pi | Сценарии | NPVi (млн.руб) | Pi |
| Вариант 9 | Вариант 10 | ||||
| Оптимистический | 52,1 | 0.1 | Оптимистический | 40,3 | 0.2 |
| Умеренно-оптимистический | 42,1 | 0.2 | Умеренно-оптимистический | 35,1 | 0.1 |
| Наиболее вероятный | 26,3 | 0.3 | Наиболее вероятный | 25,5 | 0.4 |
| Умеренно - пессимистический | 16,5 | 0.2 | Умеренно - пессимистический | 13,2 | 0.2 |
| Пессимистический | -10,5 | 0.2 | Пессимистический | -7,5 | 0.1 |
Принята гипотеза о нормальном распределении результирующего показателя NPV проекта, параметр z для 95%-ной вероятности равен 1,6. Определить VaR проекта
