Методы построения схем АП

Для построения схем АП используют различные методы:

· метод логарифмирования / антилогарифмирования;

· метод широтно-импульсной модуляции;

· метод переменной крутизны;

· кольцевой модулятор на диодах;

· параболический перемножитель.

8.1.1. Метод логарифмирования / антилогарифмирования

Трудно реализуемая операция умножения сигналов заменяется операцией суммирования логарифмов сигналов с последующим антилогарифмированием (рис. 8.3).

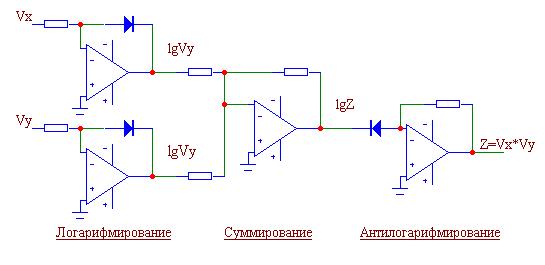
Рис. 8.3. АП с использованием логарифмирования сигналов

Используется соотношение

Z = v_xּv_y , lg Z = lg v_x + lg v_y. (8.1)

Логарифмирование может проводиться по любому основанию. В широко распространённых ранее логарифмических линейках использовались десятичные логарифмы; в современных АП часто используются натуральные логарифмы.

8.1.2. Метод широтно-импульсной модуляции

Формируется последовательность импульсов постоянной частоты f=1/(t₁+ t₂). Амплитуда импульсов U₁ пропорциональна первому сомножителю. Разность длительностей положительной и отрицательной полуволн (t₁- t₂) пропорциональна второму сомножителю (рис. 8.4).

U₁ = К₁V₁ , t₁- t₂ = К₂V₂ , t₁+ t₂ = 1/ f . (8.2)

Для среднего значения получаем выражение

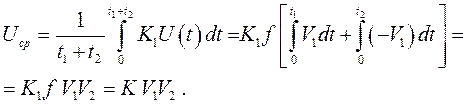(8.3)

Полученные импульсы, модулированные по амплитуде и по длительности, нужно пропустить через ФНЧ.

8.1.3. Метод переменной крутизны

Схема одноквадрантного АП, работающего при положительных значениях U_вх1 и U_вх2 , приведена на рис. 8.5.

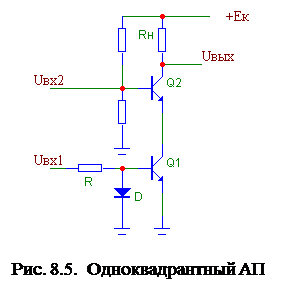Для транзистора Q₂ справедливы соотношения:

К₂ = U_вых/ U_вх2 = SR_н ,

S = I_э/φ_т = I_э/0,026,

К₂ = (I_э/0,026) R_н . (8.4)

Для транзистора Q₁

I_к1 = I_э2 = (U_вх1/R) h_21э1 . (8.5)

Подставив (8.5) в (8.4), получим

U_вых = (U_вх2U_вх1/0,026)ּh_21э1ּ(R_н / R) = КU_вх1U_вх2 . (8.6)

Схема двухквадрантного АП приведена на рис. 8.6. По сравнению со схемой одноквадрантного АП вместо транзистора Q₂ (рис. 8.5) включён дифференциальный каскад на транзисторах Q_2-1-Q_2-2 , что позволяет работать при положительных и отрицательных значениях U_вх2 .

На рис. 8.7 приведена схема четырёхквадрантного АП. Применение трёх дифференциальных каскадов позволяет работать при положительных и отрицательных значениях обоих входных сигналов.

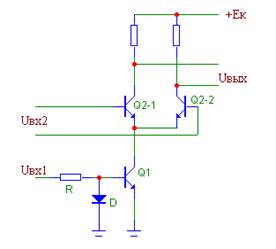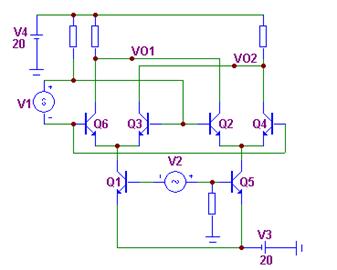Рис. 8.6. Двухквадрантный АП	Рис. 8.7. Четырёхквадрантный АП: V1 и V2 – входы, V01-V02 – выход

8.1.4. Кольцевой модулятор на диодах

Схема кольцевого модулятора на диодах с симметричными трансформаторами была рассмотрена в параграфе 7.5 (рис. 7.22). В микросхемах 235МП1, 235МП2 трансформаторы заменены резистивными делителями напряжения (рис. 8.8).

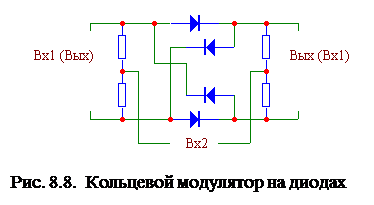Обозначим сигнал на входе Вх2 как f_к (ключевой), сигнал на Вх1 как f_с (сигнальный), тогда при одинаковом сопротивлении резисторов делителей на выходе присутствуют в основном сигналы с частотами (f_к ± f_с) и отсутствуют сигналы с частотами f_к , f_с , n f_с , а также (q_неч f_к ± p_чет f_с) и (q_чет f_к ± p_неч f_с), кроме (q_неч f_к + f_с). После фильтра НЧ останется только сигнал разностной частоты (f_к - f_с). Если амплитуда f_к достаточно велика, амплитуда НЧ сигнала U_F будет пропорциональна только амплитуде f_с :

U_F = m U_cmcos2π (f_к - f_с) t . (8.7)

8.1.5. Параболический перемножитель

Для перемножения двух чисел может быть использовано алгебраическое соотношение

xy = [(x+y)² - (x-y)²] / 4 , (8.8)

где квадраторы могут быть выполнены на диодах на основе линейно-ломаной аппроксимации. Нужно отметить, что такие перемножители имеют большую погрешность при малых входных сигналах.

8.1.6. Параметры аналоговых перемножителей

В табл. 8.1 приведены основные параметры четырёхквадрантных перемножителей К525ПС2А, К525ПС3А.

Таблица 8.1

Параметры	К525ПС2А	К525ПС3А
Погрешность перемножения ε, %	± 1,0	± 0,25
Нелинейность перемножения по координатам X, Y, % Nx Ny	± 0,8 ± 0,5	± 0,12 ± 0,1
Полоса преобразования Δfx(Δfy), МГц	0,7	0,5
Амплитуда выходного напряжения Uвых m , В	± 12	± 11

Применение АП

8.2.1. Балансный модулятор

Подадим на входы АП с коэффициентом умножения α сигналы:

U_x = U_Ω cosΩ t , U_y = U_н cosω_н t .

На выходе АП получим:

U_вых = α U_x U_x = α U_Ω U_н cosω_н t cosΩ t =

= 0,5α U_Ω U_н [cos (ω_н - Ω) t + cos (ω_н + Ω) t ] . (8.9)

Спектры входных и выходного сигналов приведены на рис. 8.9.

В спектре выходного сигнала при балансной модуляции присутствуют только боковые частоты (f_Н – f_Ω), (f_Н + f_Ω) и не расходуется мощность на передачу сигнала несущей частоты f_Н .

8.2.2. Амплитудный модулятор

Пусть на вход АП поданы сигналы

U_x = U_Ω (1+cosΩ t) , U_y = U_н cosω_н t .

На выходе АП получим

U_вых = α U_x U_x = α U_Ω U_н cosω_н tּ(1+m cosΩ t ) =

= α U_Ω U_н [cosω_н t + 0,5m cos (ω_н – Ω) t + 0,5m cos (ω_н + Ω) t ] . (8.10)

Спектры сигналов при амплитудной модуляции (АМ) приведены на рис. 8.10.

В спектре сигналов при (АМ) присутствуют несущая частота f_Н и боковые частоты (f_Н – f_Ω), (f_Н + f_Ω) и нет паразитных продуктов преобразования.

8.2.3. Амплитудный демодулятор (детектор АМ- сигналов)

Подадим на один вход АП АМ-сигнал U_x = U (1+m cosΩ t)ּcosω_н t , на другой вход – сигнал несущей частоты U_y = U_н cosω_н t .

На выходе АП получим

U_вых = α U_x U_x = α U U_н (1+m cosΩ t) ּcosω_н² t=

= 0,5ּα UU_н [1+mּcosΩ t+(1+mּcosΩ t) cos2ω_н t] . (8.11)

Спектры сигналов при АМ-демодуляции приведены на рис. 8.11.

Таким образом, с помощью АП происходит преобразование (смещение) спектра модулированного сигнала в 2 раза по частоте и одновременно выделение модулирующего сигнала f_Ω . Последний может быть затем выделен фильтром НЧ.

8.2.4. Фазовый детектор

Подадим на один вход АП ФМ-сигнал U_x = U cos[ω_н t+ φ( t)], на другой вход сигнал несущей частоты U_y = U_н cosω_н t .

На выходе АП получим

U_вых = α U_x U_x = 0,5α U U_н [ cos(2ω_н t + φ(t)) +cosφ(t)]. (8.12)

Модулирующий сигнал cosφ(t) отделяется от модулированного сигнала частоты 2ω_н фильтром НЧ. Амплитуды сигналов U и U_н нужно усилить до ограничения, тогда сигнал на выходе ФНЧ будет пропорционален cosφ(t) .

8.2.5. Использование АП для деления

На рис. 8.12 приведена схема делителя аналоговых сигналов, выполненная на АП и ОУ.

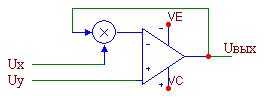
Рис. 8.12. Делитель аналоговых сигналов (схема 1)

На выходе АП имеем сигнал αU_x U_вых.:

αU_x U_вых = U_y , отсюда 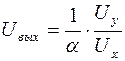. (8.13)

Другая возможная схема делителя аналоговых сигналов приведена на рис. 8.13.

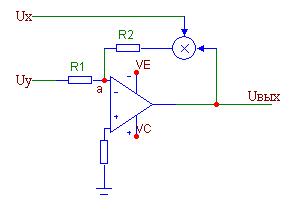
Рис. 8.13. Делитель аналоговых сигналов (схема 2)

Для точки «а» запишем закон Кирхгофа, считая, что входной ток ОУ практически равен нулю:

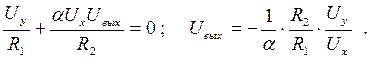
При α = R₂/R₁ имеем 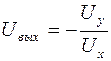. (8.14)

8.2.6 Возведение в квадрат

Чтобы возвести входной сигнал в квадрат, достаточно подать его одновременно на два входа АП (рис. 8.14).

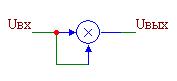
Рис. 8.14. Возведение в квадрат

U_вых = αU ²_вх . ( 8.15)

7.2.7. Извлечение квадратного корня

Включение схемы возведения в квадрат в цепь ОС операционного усилителя позволяет реализовать операцию извлечения квадратного корня (рис. 8.15).

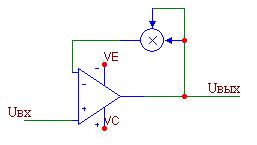
Рис. 8.15. Извлечение квадратного корня

αU ²_вых = U_вх ; 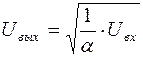, U_вх > 0. (8.16)

Глава 9. АНАЛОГОВЫЕ КОМПАРАТОРЫ

Компаратор аналоговый (КА) чувствителен к относительной полярности дифференциального напряжения, приложенного к его двум входам.

Напряжение на выходе идеального КА:

U_вых = логической «1» при (V₊ – V_-) > 0;

U_вых = логическому «0» при (V₊ – V_-) < 0,

где (V₊ – V_-) – разность напряжений между неинвертирующим и инвертирующим входами КА. По ГОСТ 17021–88 в обозначении КА присутствует подгруппа «СА» (компаратор аналоговый), например К544СА1. Изображение КА на функциональных и принципиальных схемах приведено на рис. 9.1.

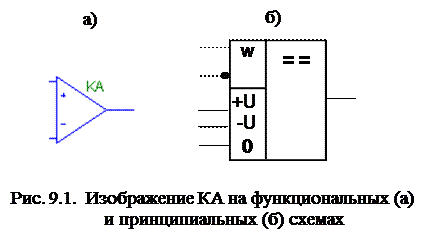На рис. 9.2 приведена характеристика «вход–выход» идеального КА.

Применение КА

Если подать на инвертирующий вход КА постоянное (опорное) напряжение U_оп , а на инвертирующий вход – входное напряжение U_вх, то получим схему обнаружителя уровня (рис. 9.3). Сигнал на выходе (уровень, соответствующий логической «единице») присутствует только тогда, когда U_вх превышает U_оп .

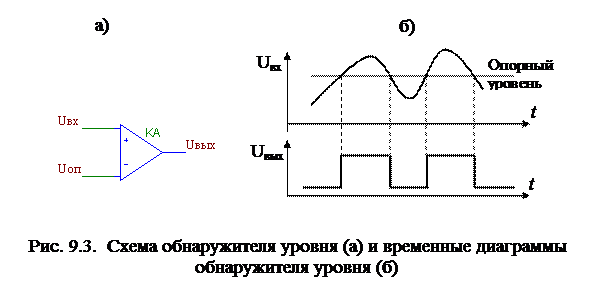Если подать на инвертирующий вход КА пилообразное напряжение, а на инвертирующий вход – входное напряжение, то получим схему широтно-импульсной модуляции сигнала (ШИМ), приведённую на рис. 9.4.