Транспортная матрица задачи №4.01
| D | E | Объем произв., шт./квартал | |||
| А | |||||
| B | |||||
| C | |||||
| Фиктивный завод | |||||
| Спрос, шт./квартал | 3700 |
Задание ЦФ
Суммарные затраты в рублях на ежеквартальную перевозку автомобилей определяются по формуле
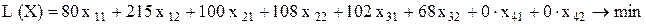
Задание ограничений
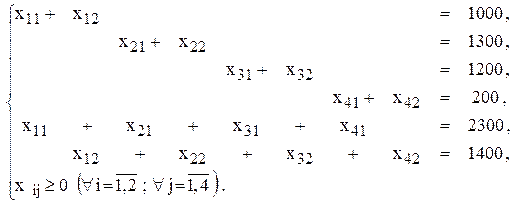[шт./квартал]
Модификации стандартной транспортной задачи
Недопустимые перевозки
Иногда в определенных направлениях перевозки продукции невозможны, например, по причине ремонта транспортных магистралей. Такие ситуации моделируются с помощью введения так называемых запрещающих тарифов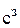 
. Запрещающие тарифы должны сделать невыгодными перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна быть больше реальных тарифов в транспортной матрице
.
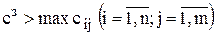Максимизация ЦФ
Существующий алгоритм решения транспортных задач (метод потенциалов) предполагает, что ЦФ стремится к минимуму. Однако существуют ситуации, когда в рамках транспортной модели требуется максимизировать ЦФ, например, общий доход, объем продаж, прибыль, качество выполняемых работ и т.д. В этом случае в модель вместо искомой ЦФ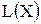 
вводится ЦФ 
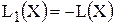, в которой тарифы умножаются на (-1). Таким образом, максимизация 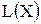будет соответствовать минимизации 
.
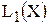Многопродуктовые модели
Если в задаче идет речь о том, что из каждого пункта отправления можно перевозить продукцию нескольких видов, то при построении модели можно использовать один из следующих вариантов:
· каждому виду продукции должна соответствовать одна транспортная матрица;
· все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции.
Варианты задач для самостоятельного решения
Задача №4.1
Постройте транспортную модель для исходных данных задачи №4.01 при условии, что квартальный спрос в пункте распределения D упал до 1900 автомобилей, а выпуск на заводе B увеличился до 1500 автомобилей за квартал.
Задача №4.2
Постройте математическую модель задачи №4.01 при условии, что за каждый недопоставленный автомобиль в распределительные центры D и E введены штрафы 200 и 300 руб. соответственно. Кроме того, поставки с завода А в распределительный центр E не планируются изначально.
Задача №4.3
Три электрогенерирующие станции мощностью 25, 40 и 30 миллионов кВт×ч поставляют электроэнергию в три города. Максимальная потребность в электроэнергии этих городов оценивается в 30, 35 и 24 миллионов кВт×ч. Цены за миллион кВт×ч в данных городах приведены в табл.4.4.
Таблица 4.4
Стоимость за электроэнергию, руб./млн.кВт×ч
| Города | ||||
| 1 | 2 | 3 | ||
| Станция | 1 | |||
| 2 | ||||
| 3 |
В августе на 20% возрастает потребность в электроэнергии в каждом из трех городов. Недостаток электроэнергии могут восполнить из другой электросети по цене 1000 за 1 миллион кВт×ч. Но третий город не может подключиться к альтернативной электросети. Электрогенерирующие станции планируют разработать наиболее экономичный план распределения электроэнергии и восполнения ее недостатка в августе. Сформулируйте эту задачу в виде транспортной модели.
Задача №4.4
Некоторой компании принадлежат три фермы, где выращивают овощи, предназначенные для последующей обработки на двух холодильных заводах компании. Одним из выращиваемых овощей являются бобы, которые холодильные заводы продают по 200 руб. за 1 т. В табл.4.5 приведены издержки производства для каждой фермы и каждого холодильного завода, максимальные значения урожая для каждой фермы, прогнозные значения спроса на следующий сезон для каждого завода. В табл.4.6 приведена стоимость транспортировки бобов.
Таблица 4.5