Метод главных компонент

При моделировании производственно-экономических процессов, чем ниже уровень рассматриваемой производственной подсистемы (структурного полразделения, исследуемого процесса), тем более характерна для входных параметров относительная независимость определяющих их факторов. При анализе основных качественных показателей работы предприятия (производительности труда, себестоимости продукции, прибыли и других показателей) приходится иметь дело с моделированием процессов со взаимосвязанной системой входных параметров (факторов). При этом процесс статистического моделирования систем характеризуется сильной коррелированностью, а в отдельных случаях почти линейной зависимостью определяющих факторов (входных параметров процесса). Это случай мультиколлинеарности, т.е. существенной взаимозависимости (коррелированности) входных параметров, модель регрессии здесь не отражает адекватно реального исследуемого процесса. Если использовать добавление или отбрасывание ряда факторов, увеличение или уменьшение объема исходной информации (количества наблюдений), то это существенно изменит модель исследуемого процесса. Применение такого подхода может резко изменить и величины коэффициентов регрессии, характеризующие влияние исследуемых факторов, и даже направление их влияния (знак при коэффициентах регрессии может измениться на противоположный при переходе от одной модели к другой).

Из опыта научных исследований известно, что большинство экономических процессов отличается высокой степенью взаимовлияния (интеркорреляции) параметров (изучаемых факторов). При расчетах регрессии моделируемых показателей по этим факторам возникают трудности в интерпретации значений коэффициентов в модели. Такая мультиколлинеарность параметров модели часто носит локальный характер, т. е. существенно связаны между собой не все исследуемые факторы, а отдельные группы входных параметров. Наиболее общий случай мультиколлинеарных систем характеризуется таким набором исследуемых факторов, часть из которых образует отдельные группы с сильно взаимосвязанной внутренней структурой и практически не связанных между собой, а часть представляет собой отдельные факторы, несформированные в блоки и несущественно связанные как между собой, так и с остальными факторами, входящими в группы с сильной интеркорреляцией.

Для моделирования такого типа процессов требуется решение проблемы о способе замены совокупности существенно взаимосвязанных факторов на какой-либо другой набор некоррелированных параметров, обладающий одним важным свойством: новый набор независимых параметров должен нести в себе всю необходимую информацию о вариации или дисперсии первоначального набора факторов исследуемого процесса. Эффективным средством решения такой задачи является использование метода главных компонент. При использовании этого метода возникает задача экономической интерпретации комбинаций исходных факторов, вошедших в наборы главных компонент. Метод позволяет уменьшить число входных параметров модели, что упрощает использование получаемых в результате регрессионных уравнений.

Сущность вычисления главных компонент заключается в определении корреляционной (ковариационной) матрицы для исходных факторов X_j и нахождении характеристических чисел (собственных значений) матрицы и соответствующих векторов. Характеристические числа являются дисперсиями новых преобразованных переменных и для каждого характеристического числа соответствующий вектор дает вес, с которым старые переменные входят в новые. Главные компоненты – это линейные комбинации исходных статистических величин. Переход от исходных (наблюдаемых) факторов к векторам главных компонент осуществляется посредством поворота координатных осей.

Для регрессионного анализа используют, как правило, лишь несколько первых главных компонент, которые в сумме объясняют от 80 до 90 % всей исходной вариации факторов, остальные из них отбрасываются. В случае если все компоненты включены в регрессию, результат ее, выраженный через первоначальные переменные, будет идентичен множественному уравнению регрессии.

Алгоритм вычисления главных компонент

Допустим, имеется m векторов (исходных факторов) размерностью n (количество измерений), которые составляют матрицу Х:

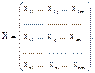
Поскольку, как правило, основные факторы моделируемого процесса имеют разные единицы измерения (одни выражены в кг, другие – в км, третьи – в денежных единицах и т. д.), для их сопоставления, сравнения степени влияния, применяют операцию масштабирования и центрирования. Преобразованные входные факторы обозначим через y_ij . В качестве масштабов выбираются чаще всего величины стандартных (среднеквадратических) отклонений:

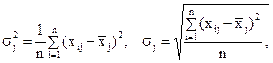
где σ_j – среднее квадратическое отклонение X_j ; σ_j² - дисперсия; 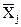- среднее значение исходных факторов в данной j-ой серии наблюдений

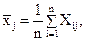
тогда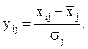

(Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания. Нормировать величину х – означает перейти к новой величине у, для которой средняя величина равна нулю, а дисперсия – единице).

Определим матрицу парных коэффициентов корреляции

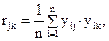
где у_ij – нормированное и центрированное значение x_j –й случайной величины для i-го измерения; y_ik – значение для k-й случайной величины.

Значение r_jk характеризует степень разброса точек по отношению к линии регрессии.

Искомая матрица главных компонент F определяется из следующего соотношения (здесь используется транспонированная ,- “повернутая на 90⁰” – матрица величин y_ij):

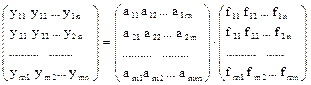
или используя векторную форму:

,

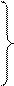
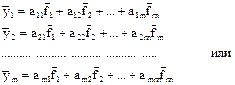
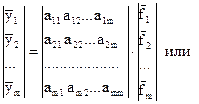
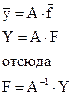где F – матрица главных компонент, включающая совокупность n полученных значений для m главных компонент; элементы матрицы А являются весовыми коэффициентами, определяющими долю каждой главной компоненты в исходных факторах.

Элементы матрицы А находятся из следующего выражения

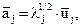
где u_j – собственный вектор матрицы коэффициентов корреляции R; λ_j – соответствующее собственное значение.

Число λ называется собственным значением (или характеристическим числом) квадратной матрицы R порядка m, если можно подобрать такой m-мерный ненулевой собственный вектор u, что Ru = λu.

Множество всех собственных значений матрицы R совпадает с множеством всех решений уравнения |R - λE| = 0. Если раскрыть определитель det |R - λE|, то получится характеристический многочлен матрицы R. Уравнение |R - λE| = 0 называется характеристическим уравнением матрицы R.

.

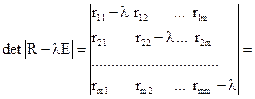
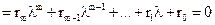Пример определения собственных значений и собственных векторов. Дана матрица .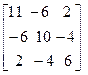

Ее характеристическое уравнение

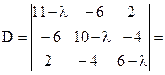
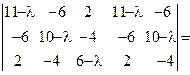
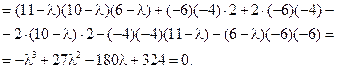
Это уравнение имеет корни λ₁=18, λ₂=6, λ₃=3. найдем собственный вектор (направление), соответствующее λ₃. Подставляя λ₃ в систему, получим:

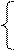8u₁ – 6u₂ +2u₃ = 0

- 6u₁ + 7u₂ - 4u₃ = 0

2u₁ - 4u₂ + 3u₃ = 0

т. к. определитель этой системы равен нулю, то согласно правилам линейной алгебры, можно отбросить последнее уравнение и решать полученную систему по отношению к произвольной переменной, например u₁ = с= 1

- 6 u₂ + 2u₃ = - 8c

7 u₂ – 4 u₃ = 6 c

Отсюда получим собственное направление (вектор) для λ₃=3

1 таким же образом можно найти собственные вектора

2 (направления) для λ₂=6 2 и λ₁=18 2

2 1 -2

-2 1

Общий принцип, лежащий в основе процедуры нахождения главных компонент показан на рис. 29.

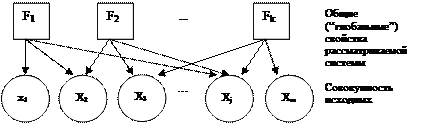Рис. 29. Схема связи главных компонент с переменными

Весовые коэффициенты характеризуют степень влияния (и направленность) данного “скрытого” обобщающего свойства (глобального понятия) на значения измеряемых показателей Х_j.

Пример интерпретации результатов компонентного анализа:

Название главной компоненты F₁ определяется наличием в ее структуре значимых признаков Х₁, Х₂, Х₄, Х₆, все они представляют характеристики эффективности производственной деятельности, т.е. F₁ - эффективность производства.

Название главной компоненты F₂ определяется наличием в ее структуре значимых признаков Х₃, Х₅, Х_7, т.е. F₂ - это размер производственных ресурсов.

ЗАКЛЮЧЕНИЕ

В пособии даны методические материалы, предназначенные для освоения экономико-математического моделирования в целях обоснования принимаемых управленческих решений. Большое внимание уделено математическому программированию, включая целочисленное программирование, нелинейное программирование, динамическое программирование, задачам транспортного типа, теории массового обслуживания, методу главных компонент. Подробно рассмотрено моделирование в практике организации и управления производственными системами, в предпринимательской деятельности и финансовом менеджменте. Изучение представленного материала предполагает широкое использование техники моделирования и расчетов с использованием комплекса программ PRIMA и в среде электронной таблицы Excel.