Потенциальное движение газированной жидкости

Газированная жидкость представляет собой смесь жидкой и газовой фаз. Газ находится не только в свободном состоянии; часть его растворена в жидком компоненте смеси. В пластовой нефти обычно содержится природный газ. Если давление в пласте выше давления насыщения нефти газом, то весь газ растворяется в нефти, а нефть называется недонасыщенной. Задача об одномерном потоке такой нефти относится к ранее описанным гомогенным задачам. Если же пластовое давление ниже давления насыщения, то в процессе движения нефти в пласте из нее выделяется газ и образуется движущаяся смесь нефти и свободного газа – газированная нефть. По мере продвижения смеси в направлении снижения давления из капельно - жидкого раствора (жидкого компонента смеси) выделяется все новая масса газа. Выделяющийся из раствора газ присоединяется к движущемуся свободному газу, вследствие чего увеличивается часть порового пространства, занимаемого газом. Свободный газ становится все более подвижным и фазовая проницаемость породы для газа растет, а фазовая проницаемость для жидкой фазы уменьшается.

Вследствие этого расчеты параметров такого газо-жидкостного потока проводят на основе многофазной модели течения. Так общее дифференциальное уравнение одномерных потоков (3.3) можно применительно к капельно-жидкой фазе газированной жидкости записать следующим образом

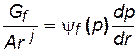, (5.12)

где .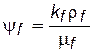

Массовый дебит газового компонента смеси G_г находится как сумма массового дебита газа, движущегося в свободном состоянии G_гс, и массового дебита газа, движущегося в растворенном состоянии G_гр. Используя формулу (3.3) для свободного газа смеси, получим:

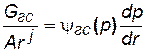, (5.13)

где 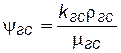– функция, в которой величины μ_гси r_гс относятся к газу.

Для газа, находящегося в растворе, найдем

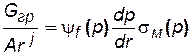, (5.14)

где σ_м(р) = G_гр/G_f – массовая растворимость газа в жидкости, т. е. количество массы газа, растворенное в единице массы жидкости при давлении р.

Суммируя почленно равенства (5.13) и (5.14), получим:

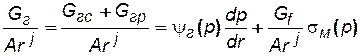, (5.15)

Для газированной жидкости пользуются при расчетах величиной объемного газового фактора Г, который представляет собой отношение объемного газового дебита Q_г, приведенного к стандартным условиям, к объемному дебиту жидкого компонента Q_ж, приведенному к тем же условиям. Поскольку массовый дебит на всех изобарических поверхностях в данном одномерном установившемся потоке один и тот же, сохраняется постоянным вдоль всего потока и газовый фактор Г.

Учитывая, что 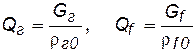, где r_г0 и r_f0 – значения плотности газа и жидкого компонента, соответственно, с помощью формул (5.13) и (5.15) получим:

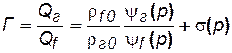, (5.16)

где объемная растворимость газа в жидкости

.

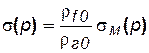Если газ однороден, то в широких пределах (примерно от 1 до 100 ат) объемная растворимость пропорциональна давлению, т. е.

σ(р) =aр, (5.17)

где a – объемный козффиииент растворимости, постоянный для данных жидкости и газа. Формула (5.17) выражает закон Генри растворимости газа в жидкости.

В соотношении для газового фактора (5.16) определим функции y_г(р) и y_f(р) в соответствии с формулой :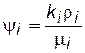

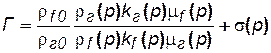, (5.18)

В практических расчетах по технологии нефтедобычи учитывается величина объемного коэффициента нефти, зависящего от давления р.

Объемный коэффициент нефти b(р) характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа. Величина b(р) есть отношение удельных объемов нефти в пластовых и атмосферных условиях.

Согласно данному определению .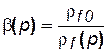

Заменяя в формуле (5.18) отношение 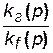функцией Y(s) получим:

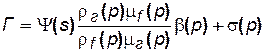, (5.19)

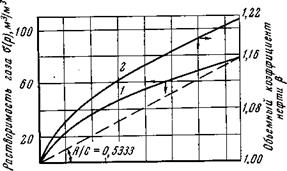Рис. 5.4 Кривые зависимости коэффициента растворимости газа в нефти и объёмного коэффициента нефти от давления

При постоянном газовом факторе Г уравнение (5.19), выражая зависимость между давлением р и насыщенностью s, служит уравнением состояния газированной жидкости. Функции μ_f(р), μ_г(p), b(р) и σ(р)определяются по экспериментальным данным. На рис. 5.4 представлены зависимости растворимости σ(р) и объемного коэффициента нефти b(р) от давления р.

Потенциальная функция для газированной жидкости имеет вид

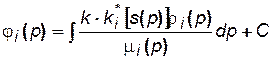(5.20)

где i=f, г; k^*_i(s) = k_i/k,смотря по тому, движение какой фазы изучается – жидкой или газовой.

Потенциальную функцию j(р) можно определить путем численного интегрирования.

Расчетные формулы для дебита по закону Дарси имеют наиболее простой вид, когда жидкость однородна и несжимаема. Такова, например, формула Дюпюи для объемного дебита Q. Придадим формуле для объемного дебита жидкой фазы газированной смеси в плоскорадиальном потоке вид формулы Дюпюи, сохранив в ней неизменным множитель р_к - р_с.

Пусть k, r_f и μ_f – постоянны. Тогда из (5.20):

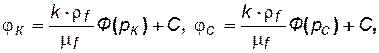(5.21)

где Ф (р_к)и Ф (p_c) – граничные значения интеграла вида .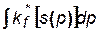

Вычитая почленно равенства (5.21) и применяя известную теорему о среднем в интегральном исчислении, получим:

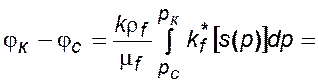, (5.22)

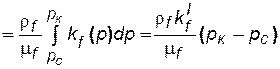
где k^'_f – некоторое среднее значение функции k_f(р) в интервале изменения р от р_с до р_к.

Подставляя полученное значение j_к-j_с в формулу (3.9) и разделяя на постоянное r_f, найдем, что:

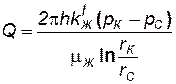. (5.23)

Имеем явное сходство с формулой Дюпюи.

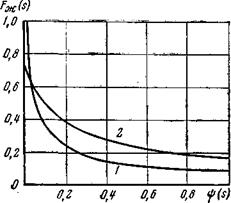
Рис.5.5. Зависимость между относительной проницаемостью для жидкости и функцией Y(s) 1– сцементированные пески; 2 – несцементированные пески

Таким образом, при расчете дебита жидкого компонента газированной жидкости можно использовать формулы для определения G или Q для однородной несжимаемой жидкости, если заменить в них проницаемость пласта k некоторым средним значением фазовой проницаемости k_f. Другими словами – определить дебит газированной жидкости можно, заменив газированную жидкость воображаемой однородной несжимаемой жидкостью, движущейся в пласте с коэффициентом проницаемости k'_f, меньшимk.

Среднее значение проницаемости k'_f определяется с помощью формулы (5.19), по которой вычисляется Y(s), соответствующее некоторому среднему давлению р_ср. Это давление можно принять равным среднему арифметическому от р_к и р_с при небольшом изменении по пласту насыщенности s. Взяв вычисленное Y(s), находим k'_f по графику на рис. 5.5.

Хотя формулы Дюпюи и (5.23) сходны между собой, это сходство чисто внешнее и они отличаются по физическому содержанию. В действительности при движении однородной несжимаемой жидкости в пласте с проницаемостью k мы на основании формулы Дюпюи можем утверждать, что дебит пропорционален депрессии Dр_с = р_к - р_с, независимо от величины давления р_к или р_с. Для газированной жидкости дебит зависит не только от депрессии Dр_с, но и от величины давления р_к или р_с. В этом легко убедиться, если вспомнить, что средняя фазовая проницаемость k'_f обусловлена значениями граничных давлений р_к и р_с.

Следует отметить, что в действительности величина средней фазовой проницаемости зависит от целого ряда параметров для жидкости, газа и пласта.

Некоторые выводы

1. Дебит газированной жидкости при прочих равных условиях всегда меньше дебита однородной несжимаемой жидкости. С повышением газового фактора при неизменяющейся депрессии Dр_с дебит жидкой фазы уменьшается, а дебит газа увеличивается; при этом показатель ε растет, хотя и непропорционально G.

2. При данной депрессии Dр_с и газовом факторе Г более высокий дебит будет при более высоком пластовом давлении. Это объясняется тем, что при более высоких давлениях меньшее количество пластового газа находится в свободном состоянии, чем при более низких давлениях. Следовательно, повышается фазовая проницаемость жидкости.

Так как для обеспечения притока нефти к забою скважин необходимо создание депрессии Dр = р_к - р_с, причем с ростом депрессии дебит скважин увеличивается, то для повышения добычи более эффективным средством является увеличение депрессии за счет повышения пластового (контурного) давления р_к, но не путем снижения забойного давления р_с.

Отмеченный факт подчеркивает большое значение своевременно принятых мер по поддержанию или повышению пластового давления в первых же стадиях разработки нефтяных месторождений.

3. Зависимость дебита жидкости и газа от депрессии, в отличие от однородной жидкости, не является линейной, хотя фильтрация каждой из фаз газированной жидкости принимается следующей линейному закону фильтрации. Таким образом, искривление индикаторной линии при фильтрации газированной жидкости еще не означает наличия отклонений от линейного закона фильтрации.

Индикаторная кривая для реальной газированной нефти имеет меньший наклон, чем кривая для идеальной газированной жидкости. Это указывает на то, что для реальной жидкости существуют добавочные сопротивления при фильтрации, не учтенные в идеальной жидкости.

4. Рассмотрение нестационарной фильтрации газированной жидкости показывает, что начальный период (первые месяцы) неустановившейся радиальной фильтрации газированной жидкости в условиях режима растворенного газа характеризуется высокими дебитами жидкости и газа. Величина дебита жидкости быстро уменьшается с течением времени. Темп падения дебита газа меньше, чем темп падения дебита жидкости.

В дальнейшем темп падения дебита жидкости резко уменьшается и наступает период относительно стабильной добычи, но абсолютная величина дебита жидкости невелика (уменьшается на порядок).Темп падения дебита газа в этот период времени уменьшается гораздо медленнее, чем темп падения дебита жидкости. Газовый фактор сначала резко возрастает, достигая в скором времени максимума, затем постепенно уменьшается.